文章目录
- 前言
- 一、搜索父节点
- 二、搜索子节点
- 三、搜索前驱后继节点
- 四、计算二叉树的高度
- 五、测试
- 总结
前言
我们接着写二叉树,在前文链接:《二叉树之二》中,我们生成了如下的有序二叉树,并且实现了插入、删除和四种遍历方法。今天我们继续实现一些二叉树的常用操作。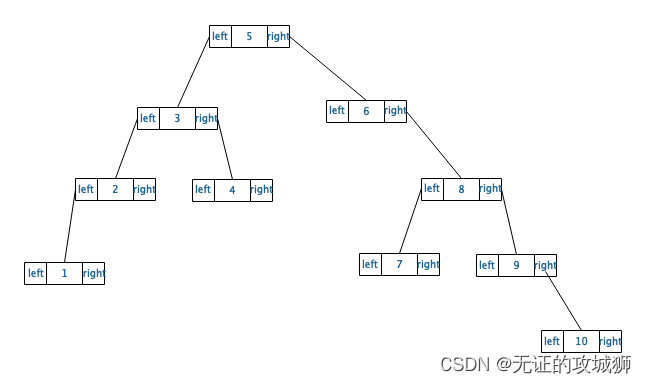
我们还用上篇文章的有序二叉树,数据也不变了:int arr[10] = {5, 3, 6, 8, 9, 2, 4, 7, 10, 1}; 如上图所示
一、搜索父节点
在开始之前,我们得在原Btree类中加一个获取值的函数,因为原二叉树的Node节点定义成私有的。
在二叉树中,搜索父节点的方法通常需要从根节点开始遍历树,直到找到目标节点的父节点。下面是一个简单的搜索父节点的方法,它接受两个参数:根节点和目标节点的值。
T getValue(Node<T>* node){
if (node == nullptr){
throw std::invalid_argument("Node is null");
}
return node->val;
}
Node<T>* findParent(T v, Node<T>* p=nullptr){
Node<T>* curr;
if (!p) curr = root;
else curr = p;
if (curr == nullptr || curr->val == v){
return nullptr;
}
if ((curr->left != nullptr && curr->left->val == v) || (curr->right != nullptr && curr->right->val == v)){
return curr;
}
if (v < curr->val){
return findParent(v, curr->left);
} else{
return findParent(v, curr->right);
}
}
该方法首先检查根节点是否为空或者是否等于目标值。如果是,则返回空指针,因为根节点没有父节点。
接下来,该方法检查根节点的左右子节点是否等于目标值。如果是,则返回根节点,因为根节点是目标节点的父节点。
如果目标值小于根节点的值,则在左子树中递归查找;否则,在右子树中递归查找。可以这样使用:
auto par = t.findParent(8);
cout << t.getValue(par) << endl;
//返回值是6
这种方法的时间复杂度为 O(h),其中 h 是树的高度。对于平衡二叉树,时间复杂度为 O(log n),其中 n 是树中节点的总数,以后再学习平衡二叉树。
二、搜索子节点
我们在二叉树类中添加一个名为 findChild 的方法来搜索子节点。这个方法接受一个 T 类型的值作为参数,表示要搜索的节点的值。它返回一个 std::pair<Node, Node> 类型的值,表示找到的子节点。如果找到了左子节点,则第一个元素为左子节点;如果找到了右子节点,则第二个元素为右子节点;如果没有找到任何子节点,则两个元素都为 nullptr。
下面是 findChild 方法的实现代码:
pair<Node<T>*, Node<T>*> findChild(T v, Node<T>* p = nullptr){
Node<T>* curr;
if (!p) curr = root;
else curr = p;
if (curr == nullptr || curr->val == v){
return make_pair(nullptr, nullptr);
}
if (curr->left != nullptr && curr->left->val == v){
return make_pair(curr->left->left, curr->left->right);
}
if (curr->right != nullptr && curr->right->val == v){
return make_pair(curr->right->left, curr->right->right);
}
if (v < curr->val) {
return findChild(v, curr->left);
} else {
return findChild(v, curr->right);
}
}
这个方法首先检查当前节点是否为空或者是否等于要搜索的值。如果是,则返回一个空的 pair 对象,表示没有找到任何子节点。
然后,该方法检查当前节点的左子节点和右子节点是否等于要搜索的值。如果找到了左子节点,则返回一个 pair 对象,其中第一个元素为左子节点的左子节点,第二个元素为左子节点的右子节点。如果找到了右子节点,则返回一个 pair 对象,其中第一个元素为右子节点的左子节点,第二个元素为右子节点的右子节点。
如果没有找到任何子节点,则该方法将在左子树或右子树中递归调用自身,以继续搜索。
我们可以使用这样使用 findChild 方法来搜索二叉树中指定节点的子节点:
auto chi = t.findChild(8);
cout << t.getValue(chi.first) << endl;
cout << t.getValue(chi.second) << endl;
返回值是7,9 实际使用中应该判断返回的是不是空节点再getValue
三、搜索前驱后继节点
在二叉搜索树中,一个节点的前驱节点是指其左子树中值最大的节点,而后继节点是指其右子树中值最小的节点。如果一个节点没有左子树,那么它的前驱节点是其第一个左祖先;如果一个节点没有右子树,那么它的后继节点是其第一个右祖先。前驱和后继节点在二叉搜索树的遍历和操作中非常有用。例如,在排序和搜索算法中,可以使用前驱和后继节点来快速定位给定值在有序二叉树中的位置。
//搜索前驱节点
Node<T>* findPre(T v, Node<T>* p = nullptr){
Node<T>* curr;
if (!p) curr = root;
else curr = p;
if (curr == nullptr){
return nullptr;
}
if (curr->val == v){
if (curr->left != nullptr){
Node<T>* temp = curr->left;
while (temp && temp->right != nullptr){
temp = temp->right;
}
return temp;
} else{
Node<T>* tmp = findParent(v);
if (tmp->right == curr){
return tmp;
} else{
while (tmp != root){
tmp = findParent(tmp->val);
if (tmp->val < v) return tmp;
}
return nullptr;
}
}
} else if (v < curr->val){
return findPre(v, curr->left);
} else{
return findPre(v, curr->right);
}
}
//搜索后继节点
Node<T>* findSuc(T v, Node<T>* p = nullptr){
Node<T>* curr;
if (!p) curr = root;
else curr = p;
if (curr == nullptr){
return nullptr;
}
if (curr->val == v){
if (curr->right != nullptr){
Node<T>* tmp = curr->right;
while (tmp && tmp->left != nullptr){
tmp = tmp->left;
}
return tmp;
} else{
Node<T>* tmp = findParent(v);
if (tmp->left == curr){
return tmp;
} else{
while (tmp != root->right){
tmp = findParent(tmp->val);
if (tmp->val > v){
return tmp;
}
}
return nullptr;
}
}
} else if (v < curr->val){
return findSuc(v, curr->left);
} else{
return findSuc(v, curr->right);
}
}
上面的代码中,findPre 和 findSuc 函数分别用于查找给定值的前驱和后继节点。
在 findPre 函数中,我们首先检查当前节点是否为 nullptr 或者是否等于给定值。如果是,则返回 nullptr。然后,我们检查当前节点的右子节点是否等于给定值。如果是,则返回右子节点的左子树中的最大值。如果不是,则根据给定值与当前节点的值的大小关系,在左子树或右子树中查找。
findSuc 函数与 findPre 函数类似,只是将右子节点和左子树替换为左子节点和右子树。返回的也是节点指针,用 getValue 方法可以得到值。需要注意的是本文的getValue方法遇到空指针会抛出错误。
可以看出搜索前驱和后续节点非常麻烦,那么有没有别的方法来实现呢?这就是另一种特别的二叉树结构,线索二叉树,线索二叉树就是把除第一个和最后一个节点外的nullptr指针换成指向本节点的前驱(左)或后续(右)因为和树的左右指针一样都是指针,为了区分是左右指针还是前驱后续指针,可以在节点类中加二个识别标志,比如0是左右指针,1是前驱后续指针这样子。一次性将前驱不是自己左指针后的节点、后续不是自己右指针后的都标好,在遍历的时候可以加快速度。
四、计算二叉树的高度
二叉树的高度等于其左右子树中最高的加一,计算二叉树的高度在算法上有很多用处。例如,可以用来判断一棵树是否平衡,也可以用来优化搜索算法等。
int getDepth(Node<T>* p = nullptr){
Node<T>* curr;
if (!p) curr = root;
else curr = p;
if (curr == nullptr) return 0;
stack<pair<Node<T>*, int>> s;
s.push({root, 1});
int maxDepth = 0;
while (!s.empty()){
Node<T>* curr = s.top().first;
int depth = s.top().second;
s.pop();
maxDepth = max(maxDepth, depth);
if (curr->left != nullptr) s.push({curr->left, depth + 1});
if (curr->right != nullptr) s.push({curr->right, depth + 1});
}
return maxDepth;
}
这个函数使用一个栈来实现DFS算法。它首先将根节点和深度1压入栈中。然后,当栈不为空时,函数弹出栈顶元素,并更新最大深度。接着,如果当前节点的左右子节点不为空,则将它们和深度加1压入栈中。最后,函数返回最大深度作为二叉树的高度。
在上面的代码中,当我们访问根节点的左右子节点时,我们会将它们的深度加1,然后将它们和新的深度压入栈中。这样,当我们再次访问这些子节点时,它们的深度就会正确地增加。
五、测试
int main(){
int arr[10] = {5, 3, 6, 8, 9, 2, 4, 7, 10, 1};
Btree<int> t;
for (int i=0; i<10; ++i) t.insert(arr[i]);
//t.preOrder();
//cout << endl;
t.inOrder();
cout << endl;
//t.postOrder();
//cout << endl;
//t.layOrder();
auto par = t.findParent(8);
cout << t.getValue(par) << endl;
auto chi = t.findChild(8);
cout << t.getValue(chi.first) << endl;
cout << t.getValue(chi.second) << endl;
auto pre = t.findPre(4);
cout << t.getValue(pre) << endl;
auto suc = t.findSuc(6);
cout << t.getValue(suc) << endl;
cout << t.getDepth() << endl;
return 0;
}
注意,文中省略了代码:#include <stack>、#include <algorithm>、using namespace std;
总结
本文介绍了关于有序二叉树的一些有用的扩展方法,比如搜索前驱后续节点可以用于查找树中小于且最接近某个值的节点,或大于且最接近的。熟练掌握这些方法,有助于后面更复杂的二叉树的学习。当然还有一些诸如将一棵二叉树插入为另一棵树的子树、求左子树或右子树的高度等文中未写的方法也值得掌握。主要是文章太长了,而且好像没人爱看,越复杂的东西看的人越少,虽然这个基本搜索二叉树也不见得有多复杂,只是相对代码量相对较多且充满了递归思想的代码。