文章目录
- 岛屿数量问题
- 方法一:采用递归的方法
- 方法二:使用并查集的方法(map)
- 方法三:使用并查集的方法(数组)
岛屿数量问题
测试链接:https://leetcode.com/problems/number-of-islands/
方法一:采用递归的方法

遇到1后将其周围的感染成2


将感染的改成2,这个很重要,否则递归跑不完。
public static int numIslands3(char[][] board) {
int count = 0;
//遍历整个二维数组,碰到‘1’字符就将其上下左右四个区域是‘1’的都感染为‘2’.
for (int i = 0; i < board.length; i++) {
//注意二维数组列数的写法。
for (int j = 0; j < board[i].length; j++) {
//被感染的变成了2,下次就不会再进入了。
if (board[i][j] == '1') {
infect(board, i, j);
count++;
}
}
}
return count;
}
public static void infect(char[][] board, int i, int j) {
//二维数组的行和列的获取方式:
//board.length -> 二维数组board中一维数组的个数,表示的是行数。
//board[0].length -> 二维数组中一维数组的元素的个数,表示的是列数。
if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] != '1') {
return;
}
board[i][j] = 2;
//将其上下左右区域都感染。
infect(board, i, j + 1);
infect(board, i, j - 1);
infect(board, i + 1, j);
infect(board, i - 1, j);
}
方法二:使用并查集的方法(map)

因为map特性的原因如果都是1字符,map只会放下一个。所以我们创建一个Dot表,来替换原broad表。
/**
* 方法二:采用并查集的方法
* 注意是map形式的并查集,使用并查集合并,一次只能合并两个。
*/
public static int numIslands1(char[][] board) {
//board数组的行与列数。
int H = board.length;
int L = board[0].length;
List<Dot> dotList = new ArrayList<>();
Dot[][] dots = new Dot[H][L];
//先遍历一遍board二维数组,将dots二维数组生成好。
//之前board数组是1的位置,现在在dots数组中是一个地址,之前在board数组中是0的位置,现在在dots数组中是null.
for (int i = 0; i < H; i++) {
for (int j = 0; j < L; j++) {
if (board[i][j] == '1') {
dots[i][j] = new Dot();
dotList.add(dots[i][j]);
}
}
}
//创建并查集并初始化并查集。其中每一个Dot都是一个小集合。
UnionFind<Dot> unionFind = new UnionFind<>(dotList);
//再遍历一遍board二维数组
for (int i = 0; i < H; i++) {
for (int j = 0; j < L; j++) {
//如果遇到了'1'就判断当前节点的左侧与上侧是否也是‘1’,如果也是‘1’就合并所对应的dots数组的中dot.
if (board[i][j] == '1') {
//加入防止左侧越界的条件。
if (j - 1 >= 0 && j - 1 < L && board[i][j - 1] == '1') {
unionFind.union(dots[i][j], dots[i][j - 1]);
}
加入防止上侧越界的条件。
if (i - 1 >= 0 && i - 1 < H && board[i - 1][j] == '1') {
unionFind.union(dots[i][j], dots[i - 1][j]);
}
}
}
}
return unionFind.sets();
}
public static class Dot {
}
public static class UnionFind<V> {
/**
* 属性
*/
public HashMap<V, V> fatherMap;
//father:<v1,v2>:指的是:v1的父亲是v2,注意这里的父亲是直系父亲.
//HashMap<5, 2>:5->2
//HashMap<2, 4>:2->4
//HashMap<4, 6>:4->6
public HashMap<V, Integer> sizeMap;
//size:<V,Integer>:size里面装的是所有集合的头部节点,以及该头部节点下集合的元素个数。
//注意不是头部节点不可以放入size中。
/**
* 构造器
*/
public UnionFind(List<V> list) {
//创建两个map。
fatherMap = new HashMap<>();
sizeMap = new HashMap<>();
//遍历一遍链表,将链表中的数据放入两个map中。
for (V l : list) {
//当只有一个节点的时候,这个节点的头部节点是他自己,即自己指向自己。
fatherMap.put(l, l);
sizeMap.put(l, 1);
}
}
/**
* findAncestor方法
* 传入一个节点,然后从这个节点开始一直往上找,直到直到最上边为止,返回最上面的节点。
*/
public V findAncestor(V cur) {
//创建一个容器,顺着当前的节点cur开始往上找,将途中经过的节点都放入这个容器中。
Stack<V> path = new Stack<>();
//循环的条件是:当当前节点的父亲就是当前节点时,说明来到了最顶部。
while (cur != fatherMap.get(cur)) {
//将cur讲过的节点放入容器中。
path.push(cur);
//cur来到其直系父亲节点。
cur = fatherMap.get(cur);
}
//这是一个优化部分。
//我们将途径的每个节点都指向祖先节点,这样就降低了路径的长度,使复杂度更低。
//假设从cur开始到顶部的长度是n,第一次进行向上寻找的时候复杂度是O(n),但是以后寻找的时候复杂度就会变成O(1)。
while (!path.isEmpty()) {
fatherMap.put(path.pop(), cur);
}
return cur;
}
/**
* isSameSet方法
* 传入两个值,判断这两个值是否是在一个集合里。
*/
public boolean isSameSet(V value1, V value2) {
return findAncestor(value1) == findAncestor(value2);
}
/**
* union方法
* 给你两个值,将两个值所在的集合进行合并。
*/
public void union(V a, V b) {
//father1指向的是a元素所在集合的头部节点。
//father2指向的是b元素所在集合的头部节点。
V father1 = findAncestor(a);
V father2 = findAncestor(b);
if (father1 != father2) {
//size1是头部节点father1所在集合的大小。
//size2是头部节点father2所在集合的大小。
int size1 = sizeMap.get(father1);
int size2 = sizeMap.get(father2);
//big指向的是集合元素多的头部节点。
//small指向的是集合元素少的头部节点。
V big = size1 > size2 ? father1 : father2;
V small = big == father1 ? father2 : father1;
//small指向big
//这里使用map实现的指针的功能。
//因为small合并到big中,所以big这个头部节点的sizemap中元素个数要增多。
sizeMap.put(big, size1 + size2);
//与此同时头部节点small应该指向big。
fatherMap.put(small, big);
//因为small指向big所以,small不再是头部节点,就将small从sizeMap中删除。
sizeMap.remove(small);
}
}
/**
* sets方法
* 返回的是一共有几个集合/几个头部节点。
*/
public int sets() {
return sizeMap.size();
}
}
}
方法三:使用并查集的方法(数组)
但其实用一维坐标是比较常见的写法。不同的1,希望用办法来区分。可以用一维坐标代表,也可用一个类的实例的不同内存地址来代表。都可以。更推荐一维坐标的方式。因为快。常数时间少。
采用并查集(数组)的方法进行操作,习惯上是采用一维数组,所以我们要将二维数组转化成一维数组。
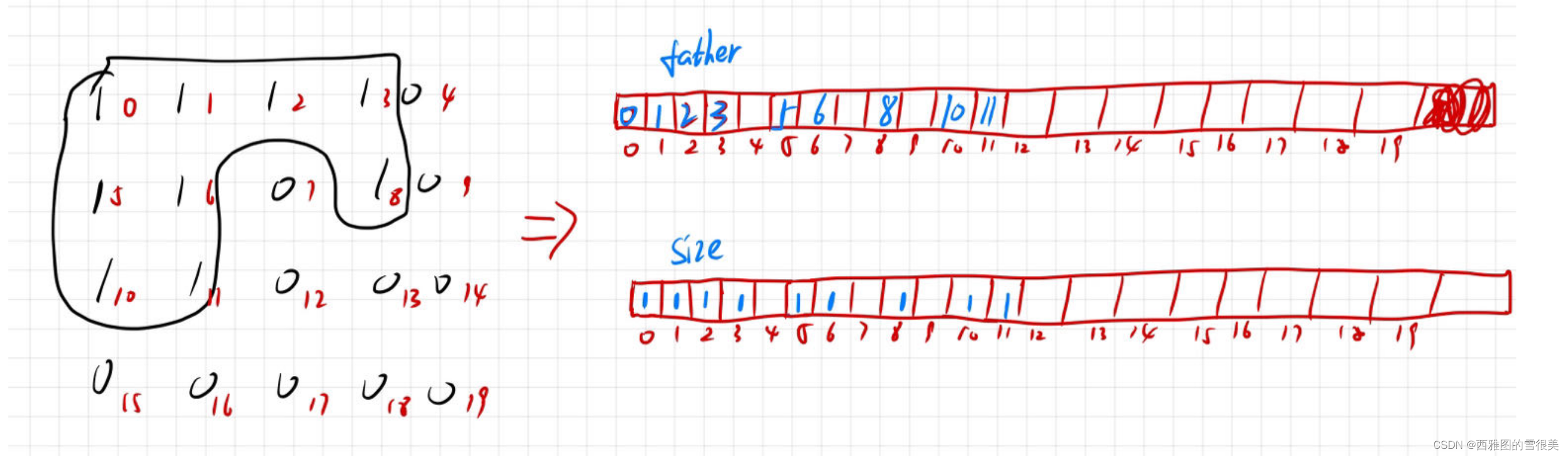
虽然一维数组上有很多的空间是没用用上的,但其实无所谓,因为这样我们可以快速的锁定我们要找的位置。
而不需要进行复杂的转换。
/**
* 方法三
*/
public static int numIslands2(char[][] board) {
UnionFind2 unionFind2 = new UnionFind2(board);
int H = board.length;
int L = board[0].length;
for (int i = 0; i < H; i++) {
for (int j = 0; j < L; j++) {
//如果遇到了'1'就判断当前节点的左侧与上侧是否也是‘1’,如果也是‘1’就合并
if (board[i][j] == '1') {
//加入防止左侧越界的条件。
if (j - 1 >= 0 && j - 1 < L && board[i][j - 1] == '1') {
unionFind2.union(i, j, i, j - 1);
}
加入防止上侧越界的条件。
if (i - 1 >= 0 && i - 1 < H && board[i - 1][j] == '1') {
unionFind2.union(i, j, i - 1, j);
}
}
}
}
return unionFind2.sets();
}
/**
* 并查集内部类
* 这里的并查集是一个二位数组改成一维数组的并查集。
*/
public static class UnionFind2 {
/**
* 属性
*/
public static int L;//列数
public static int[] fatehr;
public static int[] size;
public static int[] help;
public static int sets;
/**
* 构造器
*/
public UnionFind2(char[][] board) {
//行数
int H = board.length;
//列数
int L = board[0].length;
this.L = L;
fatehr = new int[H * L];
size = new int[H * L];
help = new int[H * L];
sets = 0;
//遍历一遍board二维数组。
for (int i = 0; i < H; i++) {
for (int j = 0; j < L; j++) {
//只有二维数组board是’1‘的,一维数组才会放入数。
//这样一维数组就会有很多位置是空的,但是这不重要。
if (board[i][j] == '1') {
//将二维数组下标转化为一维数组的下标。
int k = index(i, j);
fatehr[k] = k;
size[k] = 1;
sets++;
}
}
}
}
/**
* index方法
* 将一个二维数组坐标[i][j]转化成一维数组坐标[k]。
* 公式:i * L + j
*/
public static int index(int i, int j) {
return i * L + j;
}
/**
* findAncestor方法
*/
public static int findAncestor(int x) {
int j = 0;
while (fatehr[x] != x) {
help[j++] = x;
x = fatehr[x];
}
// father[x] == x
//优化:将途径的节点直接连到祖先节点上,从而降低了下次查找的长度。
j--;
while (j > 0) {
fatehr[help[j--]] = x;
}
return x;
}
/**
* union方法
* 将二维数组中board[i][j]与board[m][n]位置的集合进行合并
*/
public static void union(int i, int j, int m, int n) {
//将二维数组坐标[i][j]转化成一维数组坐标[k1]。
int k1 = index(i, j);
//将二维数组坐标[m][n]转化成一维数组坐标[k2]。
int k2 = index(m, n);
//找到k1的祖先fatherK1
int fatherK1 = findAncestor(k1);
//找到k2的祖先fatherK2
int fatherK2 = findAncestor(k2);
if (fatherK1 != fatherK2) {
//找到头部节点fatherK1所在集合中的元素个数
int sizeK1 = size[fatherK1];
//找到头部节点fatherK2所在集合中的元素个数
int sizeK2 = size[fatherK2];
int big = sizeK1 > sizeK2 ? fatherK1 : fatherK2;
int small = big == fatherK1 ? fatherK2 : fatherK1;
//将集合元素小的头部节点挂到集合元素比较多的头部节点上。
fatehr[small] = big;
size[big] = sizeK1 + sizeK2;
size[small] = 0;
sets--;
}
}
/**
* 因为本题并不涉及到查找两个元素是否在同一个集合中,所以省略该方法。
*/
/**
* 返回集合元素的个数
*/
public static int sets() {
return sets;
}
}

![深度学习进阶篇[8]:对抗神经网络GAN基本概念简介、纳什均衡、生成器判别器、解码编码器详解以及GAN应用场景](https://img-blog.csdnimg.cn/img_convert/c530a112c911329eaf8cb9cfeaab09fc.png)