回归测试最小化(贪心算法,帕累托支配)

介绍
有时我们不能只是重新运行我们的测试（例如，当我们
换界面）。
回归测试可能很昂贵:
(1)一些公司通宵运行回归测试套件。
(2) 对于嵌入式系统，我们可能必须测试正在使用的软件，例如 汽车或飞机, 这可能需要几个月的时间。
(3) 自动驾驶汽车的回归测试？ 模拟测试有帮助，但不是完整的解决方案。
有兴趣找到选择回归测试套件子集的好方法。
类似的问题出现在持续集成中。

我们可能会选择只运行一些测试用例：
我们最小化测试套件。通常基于标准
我们可以对测试用例进行排序（优先排序）：
目的是，如果发生故障，则很可能在早期发生测试。允许开发人员更早地解决故障

测试套件最小化中的问题
(1) 我们假设我们已经得到了一个测试套件 T。
(2) 我们要找到满足某些性质（例如覆盖率）的T 的最小子集T0。
(3) 理想情况下，保证 T0 与 T 一样有效。
(4) 大多数方法提供较弱的保证

删除冗余测试用例
(1) 当我们根据系统的变化进行回归测试时，可以使用这个概念。
(2) 要求我们已经记录了每个测试用例执行了什么代码：
这些信息可以在测试用例被收集时收集
以前用过。
(3) 我们只使用执行更改（或删除）代码的测试用例。
(4) 其他测试用例应该是多余的（这些测试用例的行为应该没有变化）

测试套件最小化的一般方法
(1) 其他方法旨在保护某些属性。
(2) 大部分重点都放在代码覆盖率上（例如分支覆盖率）。
(3) 那么问题是：
找到回归测试套件 T 的最小子集 T0，使得 T0 和 T 具有相同的覆盖率。
(4) 希望保持覆盖范围可以使我们保持有效性。
注意：如果测试执行的成本不同，那么我们可能想要一个最便宜（执行）的测试套件，而不是最小的测试套件。

正式化覆盖范围的使用
假设我们有覆盖项 C = {c1,…,ck}（例如分支），测试站点 T = {t1,…,tn} 覆盖了所有这些，并且每个 ti 属于 T 覆盖了给定的覆盖项集 Cti .
优化问题是：找到 T 的最小子集 T0，使得：

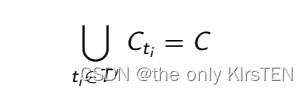
这对应于NP-complete Set Cover problem。

Set Cover 问题是计算机科学和数学中的经典计算问题。 它属于一类称为 NP-complete 问题的问题，NP-complete 问题是一组尚未找到可以在多项式时间内解决所有实例的有效算法的问题。
集合覆盖问题可以定义如下：给定一个由 n 个元素组成的宇宙集合 U 和 U 的子集 S1, S2, …, Sk 的集合，从 S 中找到并集覆盖所有元素的子集的最小数量 在美国
换句话说，我们试图从 S 中找到子集的最小可能子集，使得它们的并集包含 U 中的所有元素。S 中的每个子集可能覆盖一组不同的元素。
已知集合覆盖问题是 NP 完全问题，这意味着它不太可能有多项式时间算法来解决问题的所有实例。 这意味着随着问题规模的增加，找到最佳解决方案所需的时间呈指数增长。

精确解决方案
优化问题是 NP 完全问题。
测试套件通常很大（否则我们不需要最小化它们！）。
所以：我们的问题实例通常很大。
通常无法准确解决问题：我们只能依靠启发式方法。

一个简单的贪心算法
从空集开始。
添加一个涵盖大多数项目的测试用例 t 并从中尚未使用的集合删除 t
在每次迭代中，添加一个剩余的具有最高的覆盖率的测试用例。
当测试套件提供完全覆盖时终止。
一个简单的贪心算法并不总是一个好的方法。

更好的贪心算法
以前的贪心算法的问题在于它确实不考虑已经达到的覆盖率。
我们可以对此进行如下改进（称为 Additional Greedy
在文献中）：
从空集开始并添加其中一个测试用例涵盖大部分项目。 在每次迭代中，添加一个覆盖大多数当前未发现项目的测试用例。当测试套件提供完全覆盖时终止。
已知这种贪心算法对集合覆盖问题有效（它们提供了一个很好的近似值）

贪心算法的目标是在每一步选择覆盖最大数量未覆盖元素的子集。为了获得更好的覆盖率，改进的附加贪心算法可以从子集 A 或子集 E 开始。假设它从子集 A 开始。然后，我们选择子集 C，它涵盖元素 4。接下来，我们选择子集 D，它涵盖元素 5. 子集 C 和子集 D 各有一个额外的覆盖项目，而其他子集没有。
因此，示例顺序 A、C、D 提供了更好的覆盖率，因为它在覆盖所有元素的同时选择了更少的子集。 它减少了冗余并优化了贪婪算法实现的覆盖范围。

备择方案
还有一些工作使用元启发式算法来解决优化问题。
经常使用遗传算法的形式（但也考虑过其他类型）。

多目标方法
我们可以将问题概括为：
找到一个回归测试套件 T0，使得没有更小的测试套件提供与 T0 相同的覆盖率。
这里我们正在优化两个目标函数：
最大化覆盖范围和最小化成本
我们可以包括额外的措施，例如不同形式的覆盖，使其比贪心算法更灵活。
多目标优化算法返回一组取舍。

遗传算法 (GA) 是一类受自然选择和遗传学过程启发的优化算法。 它们用于解决复杂的优化和搜索问题。 遗传算法通过维护候选解的种群并应用选择、交叉和变异等遗传算子来创建新一代解来模拟进化过程。

以下是遗传算法通常如何工作的分步概述：

1. 初始化：初始化随机候选解的种群（通常称为个体或染色体）。 每个人都代表了问题的潜在解决方案。
2. 评价：评价种群中每个个体的适应度。 适应度函数决定解决方案在解决问题时的表现。 它分配一个数值来表示解决方案的质量。
3. 选择：根据适应度值从当前种群中选择个体。 具有更高适应性的个体更有可能被选择进行繁殖。
4. 交叉：在成对的选定个体之间进行交叉或重组，产生新的后代。 交叉涉及在个体之间交换遗传信息（或构建块）以创建其特征的新组合。
5. 突变：对后代的遗传信息进行随机改变或突变。 突变将遗传多样性引入种群，并有助于探索搜索空间的新区域。
6. 替换：用新创建的后代替换当前种群中的一些个体。 这确保人口规模保持不变。
7. 终止：重复步骤2-6，直到满足终止条件。 此条件可以是最大世代数、达到所需的适应度阈值或时间限制。
8. 输出：一旦满足终止条件，算法输出找到的最佳解，通常是适应度值最高的个体。

遗传算法特别适用于解决搜索空间大且复杂的优化问题，以及传统搜索或优化方法可能效率低下的问题。 它们已成功应用于工程设计、调度、数据挖掘和机器学习等各个领域。

比较候选解决方案
比较候选人的经典方法是帕累托支配pareto Dominance。
给定两个候选解决方案 x 和 y，我们有：
如果 x 在所有方面至少与 y 一样好，则 x 帕累托支配 y
目标，并且在至少一个目标上严格优于 y，
这意味着：就优化而言，我们永远不会选择 x。
理想情况下，我们希望找到 Pareto Front：解决方案集
不是由任何其他解决方案支配的帕累托。
有许多元启发式算法：
最著名的可能是非支配排序遗传算法 II (NSGA-II)； 现在有 NSGA-III

为了说明帕累托支配，让我们考虑一个具有两个目标的示例：最大化利润和最小化成本。 我们有两个解决方案，解决方案 A 和解决方案 B，具有以下目标值：
解决方案 A：利润 = 100 美元，成本 = 50 美元
解决方案 B：利润 = 120 美元，成本 = 60 美元
为了确定支配关系，我们比较了基于两个目标的解决方案。 在这种情况下，与解决方案 B 相比，解决方案 A 的利润较低，但成本也较低。因此，解决方案 A 不会被解决方案 B 所支配，因为它在成本方面更好。 另一方面，与解决方案 A 相比，解决方案 B 具有更高的利润和更高的成本。这意味着解决方案 B 在利润方面优于解决方案 A。
因此，解决方案 A 和解决方案 B 都不会相互支配。 它们都是帕累托最优的，因为在不牺牲另一个目标的性能的情况下，两种解决方案都不能在一个目标上得到改进。 这是帕累托前沿的示例，它表示多目标优化问题中所有非支配解的集合。