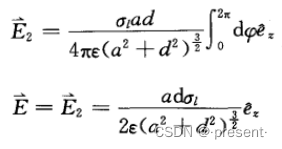目录

1.复习

2.引言 

3.数量场

1.概念

2.例题 

4.矢量场

1.概念

2.例题 

5.坐标变换和坐标单位矢

1.坐标变换

2.单位矢

---

1.复习

2.引言 

如果说矢量分析研究的是矢量的时间变化，那么场就是它的空间变化.

场是客观存在的，杨振宁先生在总结20世纪物理学时，明确指出:"场和对称性" 是两个极为重要的

革命性概念

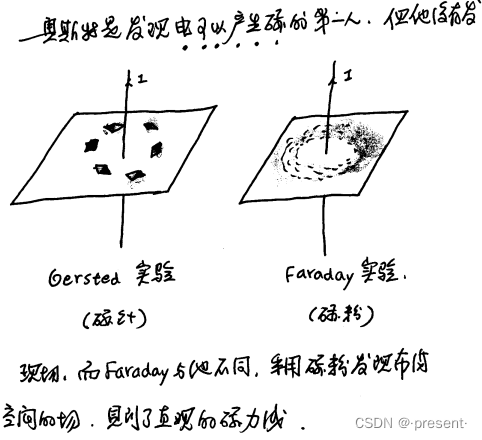
但是场是否真的存在，人们也仅仅是根据，物体处在电场或者磁场中所受到力，但周围并没有直接

接触的物体而猜想存在的.

直到法拉第改进奥斯特的实验，用磁粉替代磁针，我们才发现分布在空间的场，并且得到了直观的

磁力线

最一般的情况下，场是随时间t变化的，不过我们还是从简单到复杂，先研究清楚稳态场，即场不

随时间t变化的情况，再研究时变场.

思想：

从简单入手，再推广到复杂

从数量入手，再推广到矢量 

3.数量场

1.概念

在空间(space)中，数量函数u随点M变化

场是客观的，建立坐标系后却是主观的.

原点选取在不同位置，得到的点的坐标是不一样的.

不过有一样东西始终保持不变，就是它所对应的值，所以，我们要抓住不变量来研究.

至此我们就要引入一个关键的概念——等值面

将所有值相等的点连在一起，就可以构成一个面，我们将其称之为等值面.

比如说空间中温度场就是一个典型的数量场，每一个点都有它所对应的温度，我们将温度相同的点

连在一起，构成的面，我们称之为等温面

等值面有两大典型特征

第一.空间中的每一个点均属于一个等值面(一个点或者一条线，都可以看作一个面，这里的面是广

义的)

第二.不同等值面互不相交，即每一个点只属于一个等值面（函数不可能一个点有多个值对应）

2.例题 

例1.

山脉我们知道也是三维分布的，每一点都有其对应的高度(当然这是已经确定好一个基准平面下)

将相同高度的点连在一起，就可以构成等高线

 例2.

电场中的电位是一个标量，其实就是数量，不同点的电位就构成了电位场

现在我们想要研究点电荷产生的电位场，其实就是研究等位面.

 例3

推导二维带电无限长导线所产生的等位面.

.

还有一点需要注意的，电位对于一个三维问题来说，通常选取无穷远作为零电位点，但是二维问题

却不同，不能选择无穷远点为零电位点.

比如上面的例3，假如选取无穷远处的点作为零电位点，那r = 0,也就是导线上，由电位方程可以得

到，此时电位是无穷大的，而由于导线是无限长的，那在无穷远处，就会出现一点，即是零点位

点，又是无穷大的点位点，显然发生矛盾

4.矢量场

1.概念

有了数量场，我们就可以类比出矢量场的概念

在空间(space)中，矢量函数u随点M变化

 

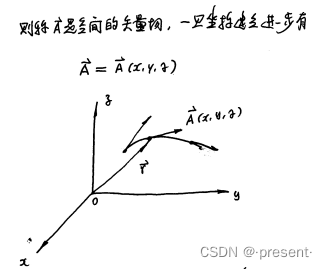
同样的，原点选取在不同位置，得到的矢量坐标是不一样的.

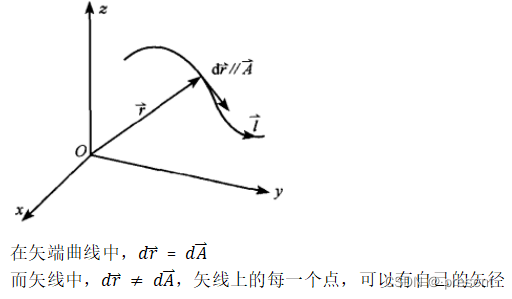
我们要像数量场一样抓住不变量来研究，对应矢量场就是我们的矢线

我们将矢量与点一一对应，将点相连就构成了矢线，当然这些点并不是随便连的，而是需要满足

dr//A(该点的矢量),即线上的每一个点，都与该点的矢量相切

同样的，矢线也有几大典型特征

1.矢线有方向，也有大小

2.矢线有起点(源),也有终点(无穷远处也能看作是终点)

3.空间中的每一个点都只属于一根矢线，除源奇异点外(矢线互不相交)

PS：矢线和矢端曲线是完全两个不同的定义

 

2.例题 

例1

我们可以简单看一个例题，求解点电荷产生的矢线(电场线)分布

先写出点电荷产生的电场强度方程

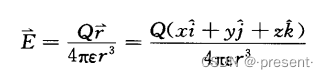
结合矢线的定义，任一一点的切线都和 

 

 

其中有两点需要指出

1.点电荷产生的电场，其大小是按照r的平方进行衰减的

2.点电荷的电力线图像是无旋的，是一个向外发散的图线 

例2

 

 

5.坐标变换和坐标单位矢

1.坐标变换

矩阵和向量是一一对应的，任意一个向量，都可以表示为矩阵的形式

以二维向量举例，两者对应关系可以这样表示

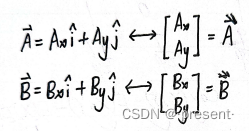
 现在我们转动坐标轴，使其变化某个角度

将原本属于y的分量投影到新的x‘轴，x分量投影到新的x'轴，就可以表示出x'分量

(同理y'分量也是这样操作)

 

 

我们又知道点积可以用矩阵的方式表示

 

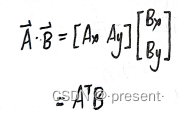
于是我们可以得到下面的关系式

  

上述最终表达式指出，点积是坐标转动的不变量

特别地，当A = B，则长度是坐标转动地不变量 

2.单位矢

在上一章我们讲到过，直角坐标系的单位矢不参与积分，导数外，对于像柱坐标系，球坐标系等等

坐标系，其单位矢都是要参与积分的.

如何解决这类问题呢？

就是将变化的单位矢，转变为我们熟悉的直角坐标系单位矢

 

同样是投影，同样把新的坐标矢，类比于上面的新坐标系

就可以将变换的单位矢，用不变单位矢来表示，从而使变化单位矢能够参与微积分

 

对于不同的参数对单位矢进行微积分，其结果我们也可以发现，不再单纯为0，甚至有可能改变单

位矢，由  

 

二阶导数也是同样的操作，其实就是相当于先求一阶导，再对相应的一阶导重复操作而已

这个结论，在电磁场计算中其实经常遇到

比如说下面的题目

 

很多教材或者讲解视频，利用的都是对称性，所有最后产生的电场，只存在z的分量

但实际上，从数学方面也可以解释

 

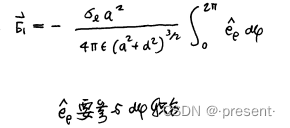
但是将其转变为不变单位矢进行微积分后，会发现这一项，其实就等于0，毕竟sin,cos沿一周期的

面积就是0

 

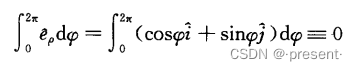
所以最后只要计算z分量即可，而ez不参与积分，可以直接提到积分外面来