先看视频1：

先看视频2：

要制作一个能顺利走到迷宫终点，并能按最短路径回来的小车，重中之重就是寻找其最短路径的算法，迷宫情况复杂多变，多个路口交错纵横，想要完美的找出最短路径并不容易，我因此总结出一套算法，能迅速找出最短路径，并适用于大多数迷宫情形，此算法对算力要求不高，不会过多阻碍主程序的运行。

在小车去终点时，我们规定小车必须优先左转，其次直走，最后右转，用暴力枚举即可到达终点。在迷宫中，把每一个线段相交的地方称作结点，经过总结，共有十字结点，正T型结点，左T型结点，右T型结点四种结点，大多数传统算法要求对每一个结点进行精准分类再分别处理，而此算法能对不同类型的结点进行统一处理。

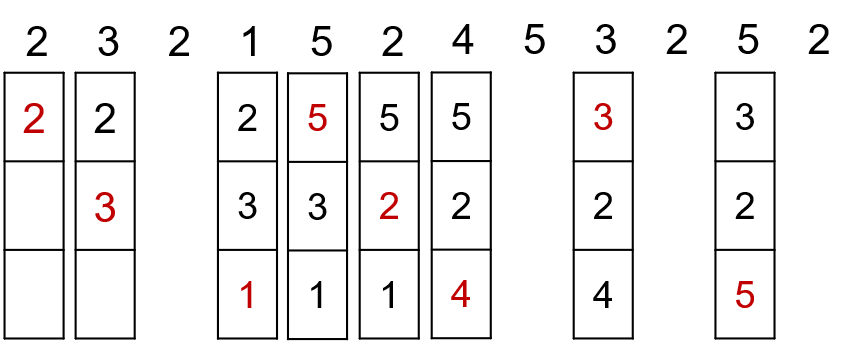
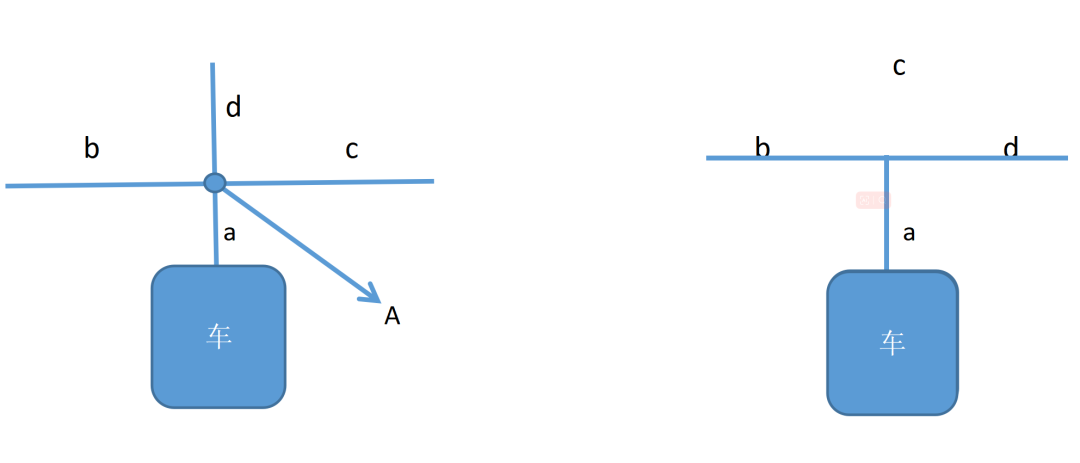
在一个结点处，小车正对且压在车身下面的那根线我们称为点a，其正对着车的左侧的线称为点b，同理，正对着车前方的直线称为点c，右侧称为点d。

把此节点称为点A（见下图），当A为1，称为无效结点，A为0，称为有效节点，考虑到有多个结点，所以A，a，b，c，d用数组表示，每个字母的初始值都为0，数组下标最大值为100。再设定一个p统计结点个数，初始值为1。此外再设置一个调头结点N，N为1则已有调头动作，否则无。小车去往终点时途经每一个结点都计算一次，在此先介绍我的结点转向算法。

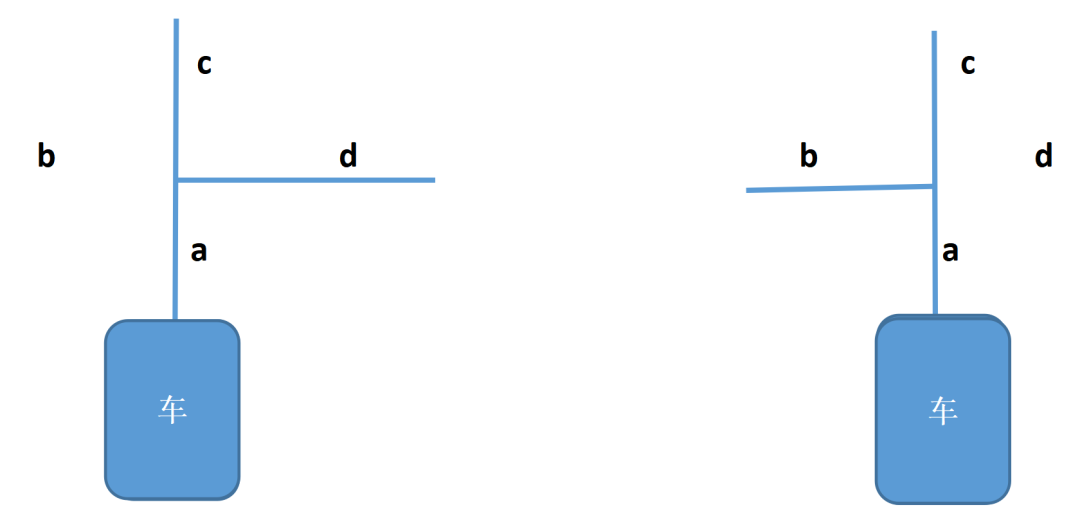
 在遇到结点时，若车左转，则：若d[p]为1，则a[p]加1，否则若c[p]为1，则d[p]加1，否则若b[p]为1，则c[p]加1，否则若a[p]为1，则b[p]加1。称此为左侧结点转向法。

在遇到结点时，若车直走，则：若b[p]为0，则c[p]加1，否则若c[p]为0，则d[p]加1，否则若d[p]为0，则a[p]加1。称此为前侧结点转向法。

在遇到结点时，计算方法为：（小车在调头动作完成后，N置1）当小车驶到一个任意结点时，若N为1，则判定此节点为原结点，p不变，此时转向时再根据情况同理调用结点转向法，此时p为p，完成转向算法后将N置0。

否则若N为0，若A[p-1]为2，则判定此结点为已过结点，p不变此时转向时继续根据情况调用结点转向法，此时p为p-1，完成转向算法后将A[p]置为0，为无效结点。

否则，则立即将a置1，此时结点状态为新节点，p加1，A[p]置为1，为有效节点，此时若车左侧有线，则调用左侧结点转向法，否则调用前侧结点转向法，此时p为p。

以上述算法走到终点时，已将所走过的每个结点都归纳到算法中，每个小车已走过的结点都有属于自己的值，用另一套算法逐个处理结点值即可计算出最短路径。

在小车回起点时，我们抛弃原有的一切算法，另起炉灶，此时要先把所有有效节点剥离出来，然后按从终点到起点的顺序将有效节点存到一个数组中，在这里先介绍我的第三种算法。

在遇到结点时，若此结点d为1，则左转，否则若c为1，则直走，否则若b为1，则右转，我称此为结点回溯法，

由此算法可顺利回到起点。因为在每一个结点计算一次，统一计算再运行，故而此算法对算力要求低，占用运行内存少，运算速度极短，不会影响其他程序的运行。

总结来说，由结点转向算法和结点回溯法即可完美走完迷宫。

但此算法可灵活处理至二级结点，对于处理n级结点写死即可，因此我优化了此算法，使其可灵活处理n个结点，算法虽简单，但写代码实践时，其中也有许多细节需要处理，但由于篇幅限制，至此不做过多赘述。

---

用心推荐，联合朋友开发了一个培训班，0基础也可以参加。对未来迷茫的同学或者朋友，可以来试试，无论是转行还是本专业的人。

只要认真完成课程，拿到一份好offer绝对不在话下。也有很多专科、双非本科院校的同学通过学习此课程拿到了一个好offer。

有兴趣的同学请加下方微信咨询：

课程大纲：