摘要: 支持向量机 (support vector machine, SVM) 有很多闪光点, 理论方面有 VC 维的支撑, 技术上有核函数将线性不可分变成线性可分, 实践上是小样本学习效果最好的算法.

1. 线性分类器

如图 1 所示, 基础的 SVM 仍然是一个线性二分类器, 这一点与 logistic 回归一致.

图 1. 基本的 SVM.

图 1 有 3 个分割线, 分别对应于一个分类器.

• $H_1$ 不能把正负样本分开, 拟合能力弱;
• $H_2$ 可以把正负样本分开 (拟合能力强), 但它与最近的正负样本距离小;
• $H_2$ 可以把正负样本分开, 而且与最近的正负样本距离达到了最大, 因此它有良好的泛化能力, 即对于新样本的预测能力, 参见 机器学习常识 4: 分类问题的训练与测试.

2. 基本方案

使用图 2 来说明.

图 2. 方案图例.

• 输入: 数据矩阵 $\mathbf{X}=(x_{ij}{)}_{n\times m}\in {\mathbb{R}}^{n\times m}$, 二分类标签向量 Y = ( y i ) n × 1 ∈ { − 1 , + 1 } n \mathbf{Y} = (y_i)_{n \times 1} \in \{-1, +1\}^n Y=(yi​)n×1​∈{−1,+1}n.
• 输出: $m$ 维空间上的一个超平面 $\mathbf{wx}+b=0$, 其中 $\mathbf{w},\mathbf{x}\in {\mathbb{R}}^m$.
• 优化目标:
  $$\arg \underset{\mathbf{w},b}{\max }\frac{1}{\Vert \mathbf{w}\Vert }.\text{\hspace{1em}(1)}$$
• 约束条件:
  $$y_i({\mathbf{w}}^{\mathsf{T}}\varphi ({\mathbf{x}}_{\mathbf{i}})+b)\ge 1.\text{\hspace{1em}(2)}$$

其中:

• 标签的取值范围为 { − 1 , + 1 } \{-1, +1\} {−1,+1}, 和 logistic 回归的 $[0,1]$ 不同. 这是为了表达相应的式子方便;
• 优化目标是最小化实线到虚线的间隔;
• 约束条件是每个样本点被正确分类 (为正数), 且到实线的加权距离不小于 1.

图 2 中:

• 实线对应的是线性分类器, 即分割超平面;
• 虚线上的点被称为支持向量 (support vector), 也就是关键样本的意思, 因为样本在空间用向量表示;
• 支持向量之外的样本, 最终没有为分类器作出贡献. 这是与 logistic 回归一个本质的区别.

3. 核函数

用核函数将低维空间的数据映射到高维空间, 这样, 以前线性不可分的数据就变得线性可分. 这是一个神奇的想法, 因为机器学习很多时候致力于将高维数据降为低维 (如 PCA, 这个我们后面说), 而 SVM 反其道而行的.

图 3. 高斯核的作用.

图 3 给出了一个例子. 原始数据点是线性不可分的 (即二维平面上的任意直线都不可能把两种类别的数据点分开). 但使用高斯核将数据映射到三维就可以做到用二维平面分割. 想像下某人脸上有痘痘, 如果脸部看作一个平面, 则去掉痘痘不可避免需要画一个圈, 它不是线性的. 现在逮住痘痘的中间往外面拉, 将脸部拉成一个曲面, 这时候, 用一把手术刀进行切割 (对应于一个平面), 就可以把痘痘切下来啦. 这真是一个不忍直视的画面 😦.
图 4 给出了更直观的画面.

图 4. 二维到三维图示.

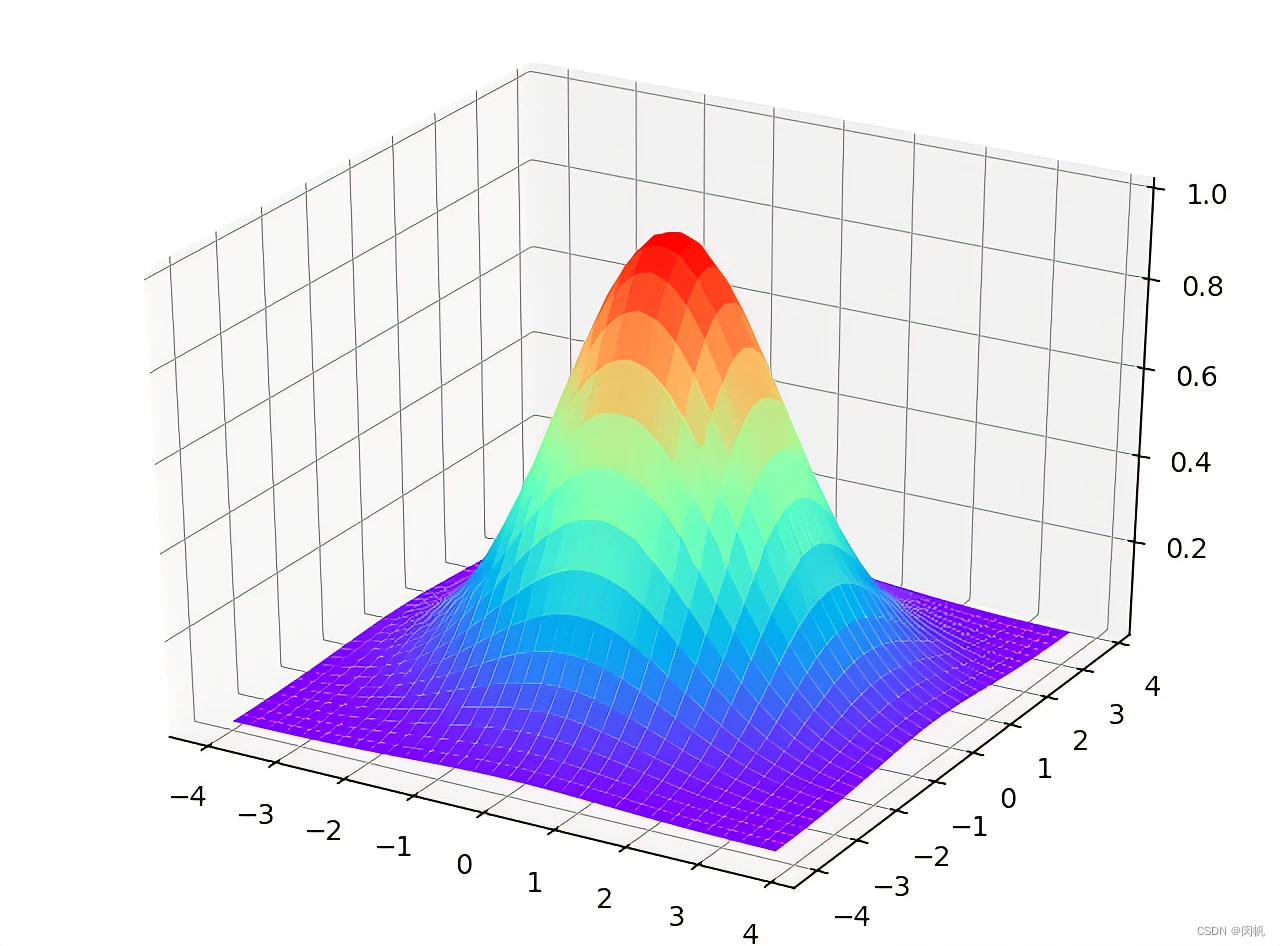
还有很多核函数. 甚至有人将核技巧弄出来之后, 脱离了 SVM 进行使用. 这是 2000 年前后的研究热点.

4. 软间隔

有时候某些正负样本实在无法从对方阵营里面分出来, 即 (2) 式所表达的约束条件无法得到满足, 就可以使用软间隔. 具体招数就不在这里描述啦.