目录
【树】
【二叉树】
二叉树的遍历
Go代码实现
二叉树的复杂度分析
【二叉搜索树】
Go代码实现
【每日一练:移除元素】
【树】
什么是树?这个不用解释了吧,马路两边种的都是树。数据结构里面的“树”和现实生活中的树类似,像一颗反过来的树,最上面是树根,下面是树的各个分枝,如下图所示:
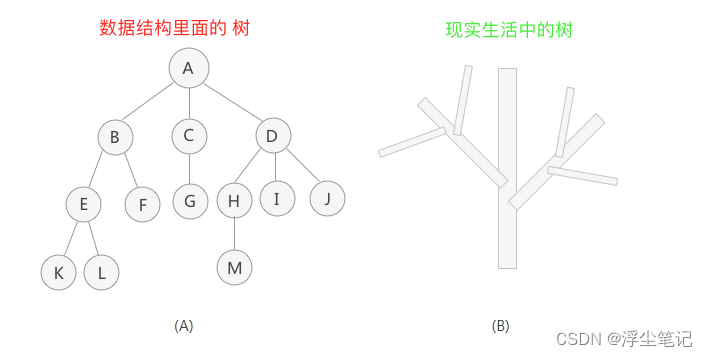
树里面的每个元素叫作“节点”,最顶端的是“根节点”(图中A是根节点),上下层级的是“父子节点”(A是B、C、D的父节点),同一层级的是“兄弟节点”(B、C、D之间是兄弟节点),最后一层是“叶子结点”(K、L、F、G、M、I、J是叶子结点)。
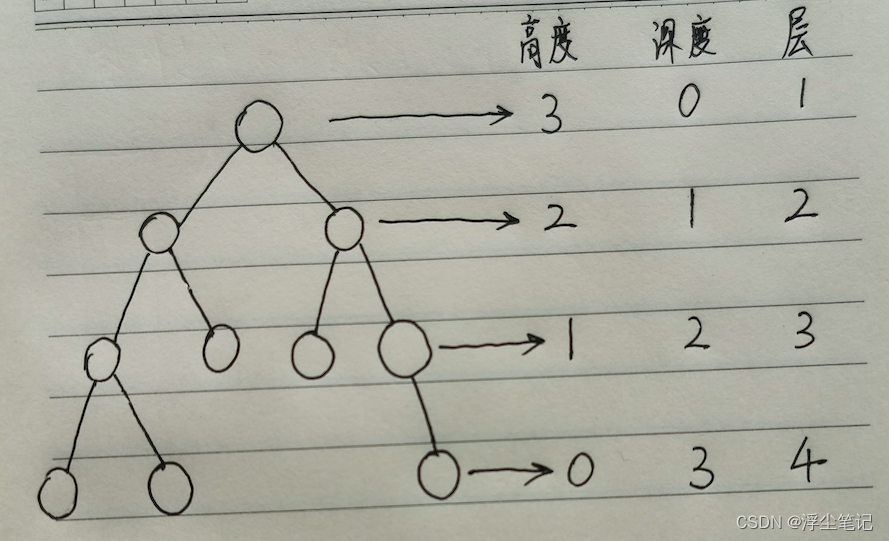
关于树的高度、深度、层数:
- 节点的高度:节点到叶子节点的最长路径(边数)
- 节点的深度:根节点到这个节点所经历的边的个数
- 节点的层数:节点的深度 + 1
- 树的高度:根节点的高度
【二叉树】
在各种各样的树中,最常用的是二叉树,每个节点最多有两个子节点,分别是左子节点和右子节点,二叉树并不要求每个节点都有两个子节点,有的只有左子节点,有的节点只有右子节点。
同理,如果每个节点有四个节点的树就是“四叉树”,有八个节点的树就是“八叉树”。
要存储一棵二叉树,可以选择基于指针的二叉链式存储法,也可以选择基于数组的顺序存储法。
链式存储的二叉树:每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节点的指针,只要拎住根节点就可以通过左右子节点的指针把整棵树都串起来。大部分二叉树代码都是通过链式结构来实现的。
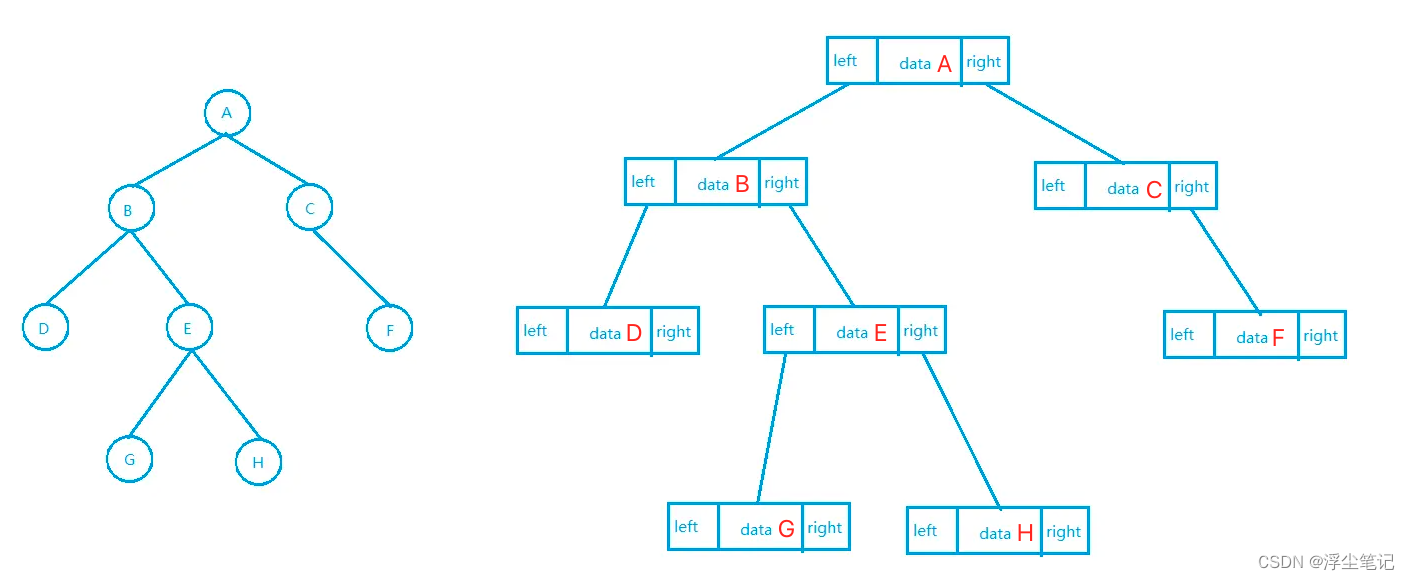
数组存储的顺序二叉树:把根节点存储在 i 的位置,左子节点就存储在 i * 2 的位置,右子节点就存储在 i * 2 + 1 的位置;反过来,下标为 i/2 的位置存储的就是对应的父节点。通过这种方式,只要知道根节点存储的位置(为了方便计算子节点,根节点会存储在下标为 1 的位置),就可以通过下标计算把整棵树都串起来。
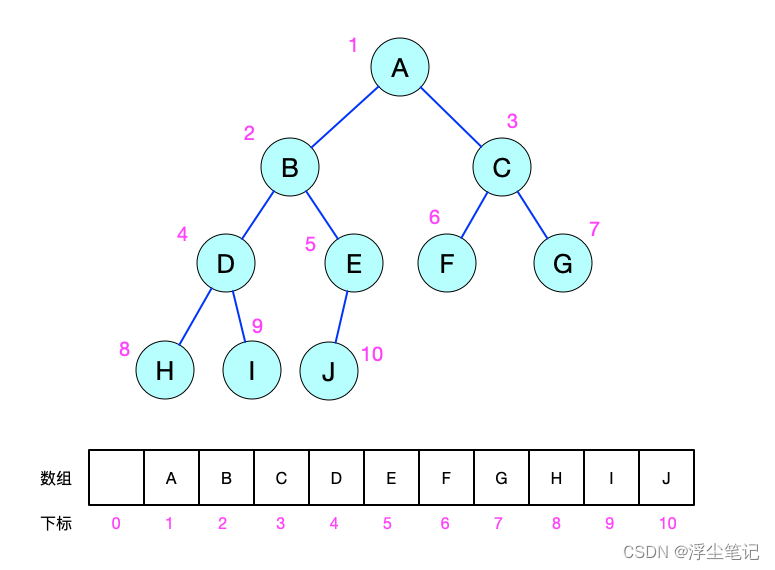
二叉树又分为:普通二叉树、满二叉树、完全二叉树、非完全二叉树等。
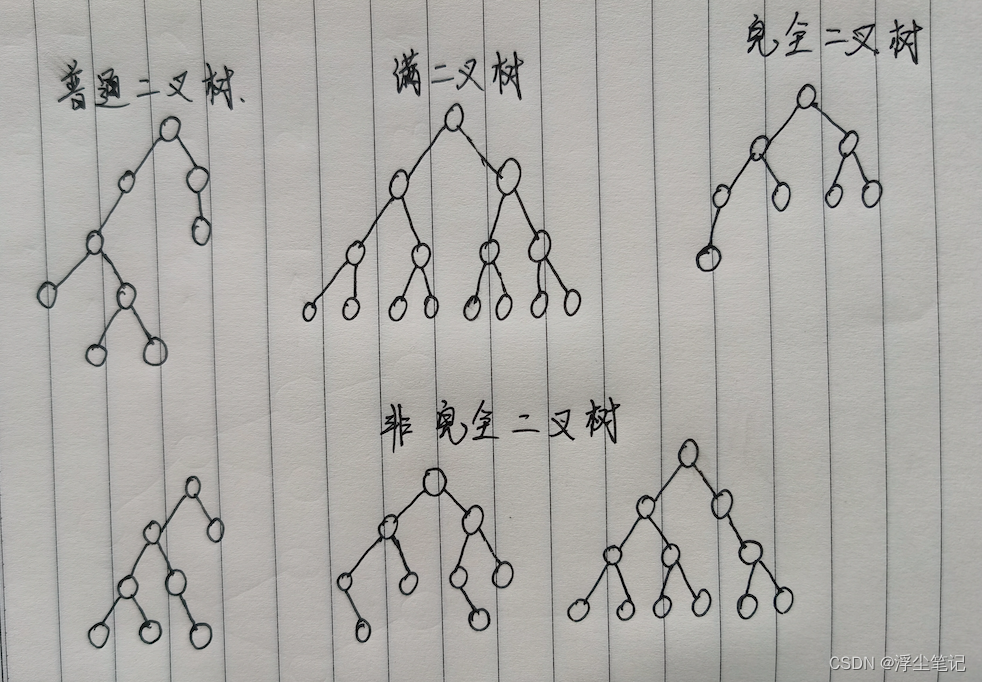
满二叉树:叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点。
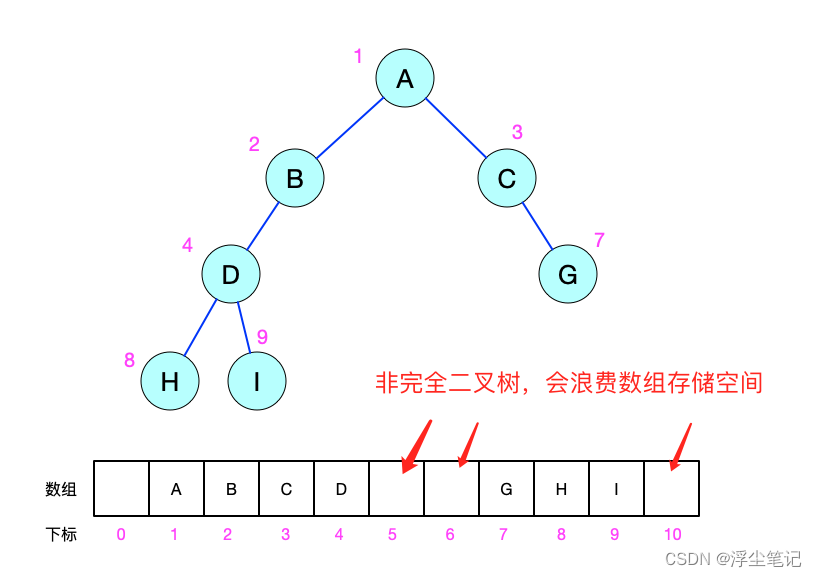
完全二叉树:叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大。最后一层叶子结点靠左排列,是为了使用数组存储的时候不浪费太多空间。比如把上面的顺序二叉树改为非完全二叉树,就会出现浪费数组空间的情况。
二叉树的遍历
遍历二叉树的三种方法:前序遍历、中序遍历、后序遍历,这里的“序”指的是根节点的遍历顺序。
-
前序遍历:先遍历根节点,然后遍历左子树,最后遍历右子树(根->左->右)。print(r) => foreach(r->left) => foreach(r->right);
-
中序遍历:先遍历左子树,然后遍历根节点,最后遍历右子树(左->根->右)。foreach(r->left) => print(r) => foreach(r->right);
-
后序遍历:先遍历左子树,然后遍历右子树,最后遍历根节点(左->右->根)。foreach(r->left) => foreach(r->right) => print(r);
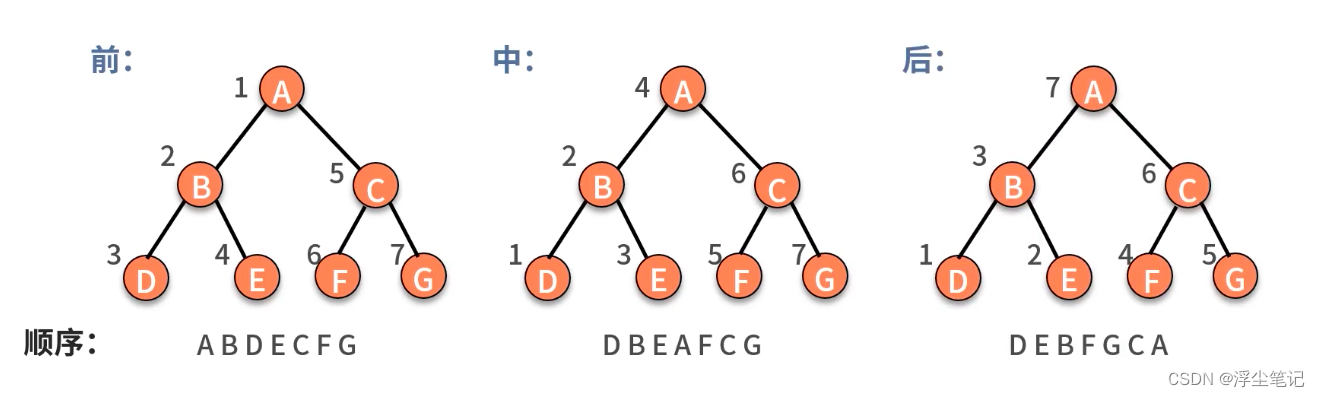
二叉树的前中后序遍历
//二叉树的前、中、后序 遍历的伪代码
//前序遍历
void preOrder(Node* root) {
if (root == null) return;
print root //打印root节点
preOrder(root->left); //打印左子树
preOrder(root->right); //打印右子树
}
//中序遍历
void inOrder(Node* root) {
if (root == null) return;
inOrder(root->left); //打印左子树
print root //打印root节点
inOrder(root->right); //打印右子树
}
//后序遍历
void postOrder(Node* root) {
if (root == null) return;
postOrder(root->left); //打印左子树
postOrder(root->right); //打印右子树
print root //打印root节点
}另外还可以对二叉树层序遍历:先遍历根节点,然后对于子节点中同一级的兄弟节点依次遍历,可以使用FIFO队列。
Go代码实现
下面是Go语言实现二叉树遍历的代码:
package main
import "fmt"
type BinaryTree struct {
Value int
LeftNode *BinaryTree
RightNode *BinaryTree
}
// 前序遍历: 根节点 ---> 左子树 ---> 右子树
func preOrder(node *BinaryTree) {
if node == nil {
return
}
fmt.Printf("%v ", node.Value)
preOrder(node.LeftNode)
preOrder(node.RightNode)
}
// 中序遍历: 左子树---> 根节点 ---> 右子树
func inOrder(node *BinaryTree) {
if node == nil {
return
}
inOrder(node.LeftNode)
fmt.Printf("%v ", node.Value)
inOrder(node.RightNode)
}
// 后序遍历: 左子树 ---> 右子树 ---> 根节点
func tailOrder(node *BinaryTree) {
if node == nil {
return
}
tailOrder(node.LeftNode)
tailOrder(node.RightNode)
fmt.Printf("%v ", node.Value)
}
// 层序遍历,从root节点一层一层的遍历
func levelOrder(rootNode *BinaryTree) {
if rootNode == nil {
return
}
var nodeSlice []*BinaryTree // 封装一个slice
nodeSlice = append(nodeSlice, rootNode)
recursion(nodeSlice) //递归遍历
}
// 递归遍历核心
func recursion(nodeSlice []*BinaryTree) {
if len(nodeSlice) == 0 { // 如果当前层级slice为空,则结束遍历
return
}
var nextSlice []*BinaryTree // 创建新的节点slice,存储下一层需要遍历的node
for i := 0; i < len(nodeSlice); i++ { //遍历当前nodeSlice
node := nodeSlice[i] //取出要遍历的node
fmt.Printf("%v ", node.Value) //输出当前node的值
if node.LeftNode != nil { //当前node左子节点append到下一层nodeSlice中
nextSlice = append(nextSlice, node.LeftNode)
}
if node.RightNode != nil { //当前node右子节点append到下一层nodeSlice中
nextSlice = append(nextSlice, node.RightNode)
}
}
recursion(nextSlice) //递归遍历下一层的nodeSlice
}
func main() {
//测试
/*
1
/ \
2 3
/ \ \
4 5 6
*/
var rootNode = &BinaryTree{
Value: 1,
LeftNode: &BinaryTree{
Value: 2,
LeftNode: &BinaryTree{
Value: 4,
},
RightNode: &BinaryTree{
Value: 5,
},
},
RightNode: &BinaryTree{
Value: 3,
RightNode: &BinaryTree{
Value: 6,
},
},
}
//前序遍历
preOrder(rootNode) //1 2 4 5 3 6
//中序遍历
inOrder(rootNode) //4 2 5 1 3 6
//后序遍历
tailOrder(rootNode) //4 5 2 6 3 1
//层序遍历
levelOrder(rootNode) //1 2 3 4 5 6
}
二叉树的复杂度分析
- 二叉树遍历过程中,函数调用栈的深度和树的高度有关,所以空间复杂度是O(H),H为树的高度。
- 二叉树遍历过程中,每个结点都被访问了一次,所以二叉树遍历的时间复杂度是O(n)。
- 二叉树中添加和删除数据时,只需要通过指针建立连接关系就可以了,所以二叉树添加和删除操作的时间复杂度是O(1)。
【二叉搜索树】
二叉搜索树又叫做 二叉查找树:在树中的任意一个节点,它的左子树中每个节点的值都要小于这个节点的值,右子树中每个节点的值都大于这个节点的值。也就是说以树的任意一个节点为分界线,左子树->当前节点->右子树 的数据由小到大。对二叉搜索树中序遍历后,可以输出一个从小到大的有序数据队列,时间复杂度是 O(n),非常高效。
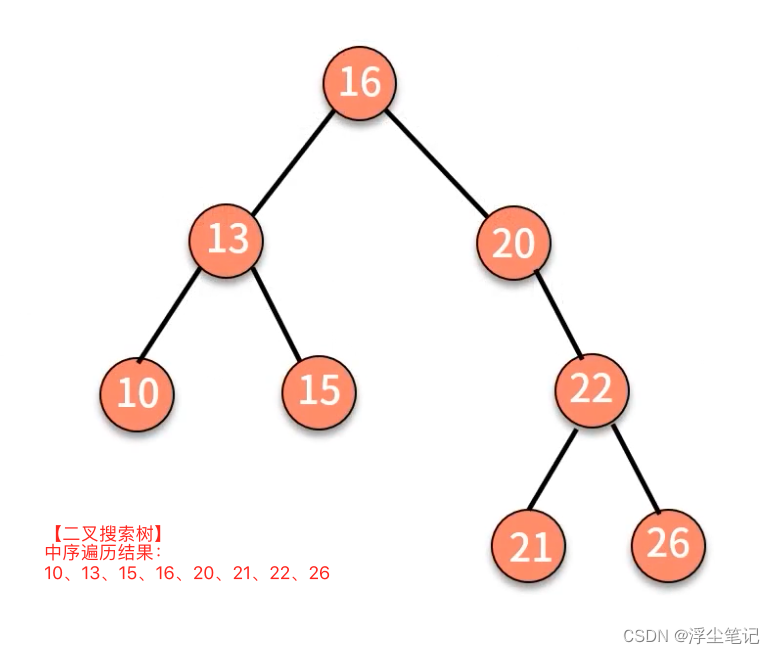
二叉搜索树的查找操作:
- 首先判断根结点是否等于要查找的数据,如果是就返回;
- 如果根结点大于要查找的数据,就在左子树中递归执行查找动作,直到查找到叶子结点;
- 如果根结点小于要查找的数据,就在右子树中递归执行查找动作,直到查找到叶子结点;
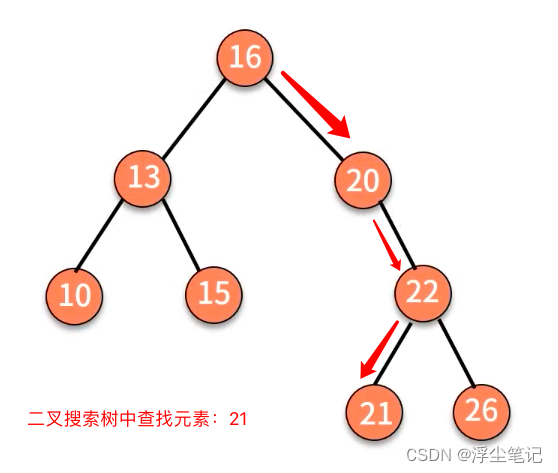
二叉搜索树的插入操作(需要先执行上面的查找操作,找到对应位置后再插入元素):
- 新插入的数据一般都是在叶子节点上,因此只需要从根节点开始依次比较要插入的数据和节点的大小关系。
- 如果要插入的数据比节点数值大,并且节点的右子树为空,就将新数据插入到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。
- 如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
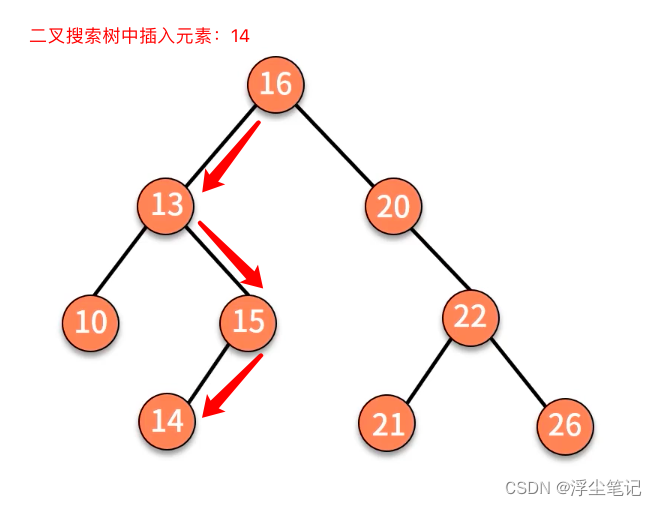
二叉搜索树的删除操作:
- 如果要删除的节点没有子节点,那么直接将父节点中指向要删除节点的指针置为 null。
- 如果要删除的节点只有一个子节点(只有左子节点或者右子节点),那么需要更新父节点中指向要删除节点的指针,让它指向要删除节点的子节点就可以了。
- 如果要删除的节点有两个子节点,需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上,然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),此时可以应用上面两条规则来删除这个最小节点。(也可以将要删除的节点标记为“已删除”,但并不真正从树中将这个节点去掉,会比较浪费内存空间)

Go代码实现
下面是Go语言实现二叉搜索树的代码:
package main
import (
"fmt"
)
// 二叉查找树根节点
type BinarySearchTree struct {
Root *BinarySearchTreeNode // 树根节点
}
// 二叉查找树节点
type BinarySearchTreeNode struct {
Value int64 // 值
Times int64 // 值出现的次数
Left *BinarySearchTreeNode // 左子树
Right *BinarySearchTreeNode // 右字树
}
// 初始化一个二叉查找树
func NewBinarySearchTree() *BinarySearchTree {
return new(BinarySearchTree)
}
// 添加元素
func (tree *BinarySearchTree) Add(value int64) {
// 如果没有树根,证明是颗空树,添加树根后返回
if tree.Root == nil {
tree.Root = &BinarySearchTreeNode{Value: value}
return
}
// 将值添加进去
tree.Root.Add(value)
}
func (node *BinarySearchTreeNode) Add(value int64) {
if value < node.Value { // 如果插入的值比节点的值小,那么要插入到该节点的左子树中
if node.Left == nil { // 如果左子树为空,直接添加
node.Left = &BinarySearchTreeNode{Value: value}
} else { // 否则递归
node.Left.Add(value)
}
} else if value > node.Value { // 如果插入的值比节点的值大,那么要插入到该节点的右子树中
if node.Right == nil { // 如果右子树为空,直接添加
node.Right = &BinarySearchTreeNode{Value: value}
} else { // 否则递归
node.Right.Add(value)
}
} else { // 值相同,不需要添加,值出现的次数加1即可
node.Times = node.Times + 1
}
}
// 查找指定节点
func (tree *BinarySearchTree) Find(value int64) *BinarySearchTreeNode {
if tree.Root == nil {
// 如果是空树,返回空
return nil
}
return tree.Root.Find(value)
}
func (node *BinarySearchTreeNode) Find(value int64) *BinarySearchTreeNode {
if value == node.Value {
// 如果该节点刚刚等于该值,那么返回该节点
return node
} else if value < node.Value {
// 如果查找的值小于节点值,从节点的左子树开始找
if node.Left == nil {
// 左子树为空,表示找不到该值了,返回nil
return nil
}
return node.Left.Find(value)
} else {
// 如果查找的值大于节点值,从节点的右子树开始找
if node.Right == nil {
// 右子树为空,表示找不到该值了,返回nil
return nil
}
return node.Right.Find(value)
}
}
// 删除指定的元素
func (tree *BinarySearchTree) Delete(value int64) {
if tree.Root == nil {
// 如果是空树,直接返回
return
}
// 查找该值是否存在
node := tree.Root.Find(value)
if node == nil {
// 不存在该值,直接返回
return
}
// 查找该值的父亲节点
parent := tree.Root.FindParent(value)
// 第一种情况,删除的是根节点,且根节点没有儿子
if parent == nil && node.Left == nil && node.Right == nil {
// 置空后直接返回
tree.Root = nil
return
} else if node.Left == nil && node.Right == nil {
// 第二种情况,删除的节点有父亲节点,但没有子树
// 如果删除的是节点是父亲的左儿子,直接将该值删除即可
if parent.Left != nil && value == parent.Left.Value {
parent.Left = nil
} else {
// 删除的原来是父亲的右儿子,直接将该值删除即可
parent.Right = nil
}
return
} else if node.Left != nil && node.Right != nil {
// 第三种情况,删除的节点下有两个子树,因为右子树的值都比左子树大,那么用右子树中的最小元素来替换删除的节点,这时二叉查找树的性质又满足了。
// 找右子树中最小的值,一直往右子树的左边找
minNode := node.Right
for minNode.Left != nil {
minNode = minNode.Left
}
// 把最小的节点删掉
tree.Delete(minNode.Value)
// 最小值的节点替换被删除节点
node.Value = minNode.Value
node.Times = minNode.Times
} else {
// 第四种情况,只有一个子树,那么该子树直接替换被删除的节点即可
// 父亲为空,表示删除的是根节点,替换树根
if parent == nil {
if node.Left != nil {
tree.Root = node.Left
} else {
tree.Root = node.Right
}
return
}
// 左子树不为空
if node.Left != nil {
// 如果删除的是节点是父亲的左儿子,让删除的节点的左子树接班
if parent.Left != nil && value == parent.Left.Value {
parent.Left = node.Left
} else {
parent.Right = node.Left
}
} else {
// 如果删除的是节点是父亲的左儿子,让删除的节点的右子树接班
if parent.Left != nil && value == parent.Left.Value {
parent.Left = node.Right
} else {
parent.Right = node.Right
}
}
}
}
// 中序遍历
func (tree *BinarySearchTree) MidOrder() {
tree.Root.MidOrder()
}
func (node *BinarySearchTreeNode) MidOrder() {
if node == nil {
return
}
// 先打印左子树
node.Left.MidOrder()
// 按照次数打印根节点
for i := 0; i <= int(node.Times); i++ {
fmt.Print(node.Value, " ")
}
// 打印右子树
node.Right.MidOrder()
}
func main() {
values := []int64{3, 6, 8, 20, 9, 2, 6, 8, 9, 3, 5, 40, 7, 9, 13, 6, 8}
// 初始化二叉查找树并添加元素
tree := NewBinarySearchTree()
for _, v := range values {
tree.Add(v)
}
fmt.Println(tree.Root.Value) //3
// 查找存在的9
node = tree.Find(9) //true
// 删除存在的9后,再查找9
tree.Delete(9)
node = tree.Find(9) //false
// 中序遍历,实现排序
tree.MidOrder() //2 3 3 5 6 6 6 7 8 8 8 13 20 40
}Golang二叉树源代码:https://gitee.com/rxbook/go-algo-demo/tree/master/tree
关于PHP中对二叉树的遍历,参考:PHP二叉树1 和 PHP二叉树2
【每日一练:移除元素】
力扣27. 移除元素(源代码:leetcode/RemoveElement.go · 浮尘/go-algo-demo - Gitee.com)
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
示例 1:输入:nums = [3,2,2,3], val = 3,输出:2, nums = [2,2]
示例 2:输入:nums = [0,1,2,2,3,0,4,2], val = 2,输出:5, nums = [0,1,3,0,4]
思路:要求原地修改数组,就不能开辟新的空间,分析如下:
- 循环遍历一次当前数组(切片),如果当前元素的值不等于 val ,就把当前元素的值重新赋值给当前数组从零开始的下标;
- 全部遍历一遍之后,所有等于val 的元素全都排到了数组的后面,然后直接返回已重新赋值的切片长度的子切片即可;
- 数组中的每个元素最多需要校验一次就可以了,因此时间复杂度是 O(N),空间复杂度: O(1)。
package main
import "fmt"
func removeElement(nums []int, val int) (int, []int) {
ret := 0
//把nums[0:ret]当做新数组,把nums数组中不等于val的元素覆盖的插入到里面
for i := 0; i < len(nums); i++ {
if nums[i] != val {
nums[ret] = nums[i]
ret++
}
}
// 返回新的数组中已经重新赋值过的长度,后面的都是传入的val
return ret, nums[0:ret]
}
func main() {
fmt.Println(removeElement([]int{3, 2, 2, 3}, 3)) //2 [2 2]
fmt.Println(removeElement([]int{0, 1, 2, 2, 3, 0, 4, 2}, 2)) //5 [0 1 3 0 4]
}