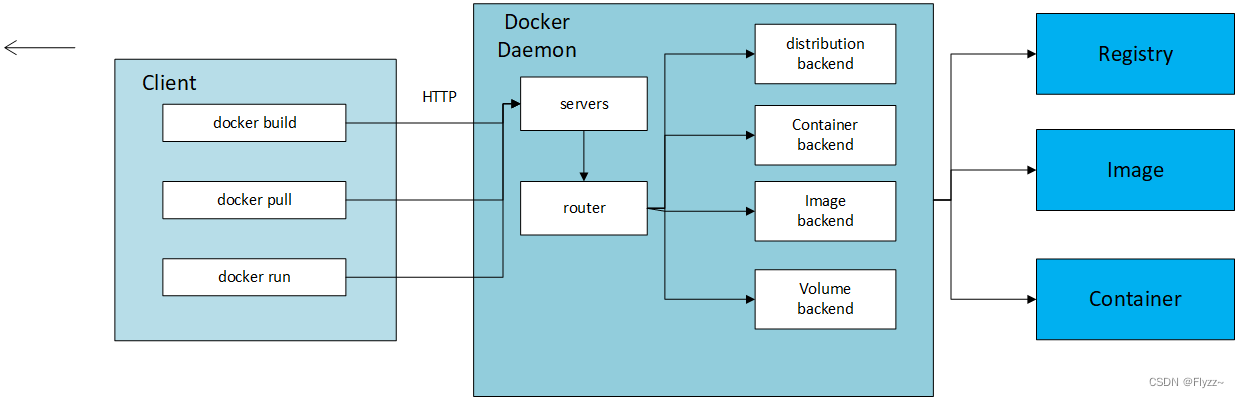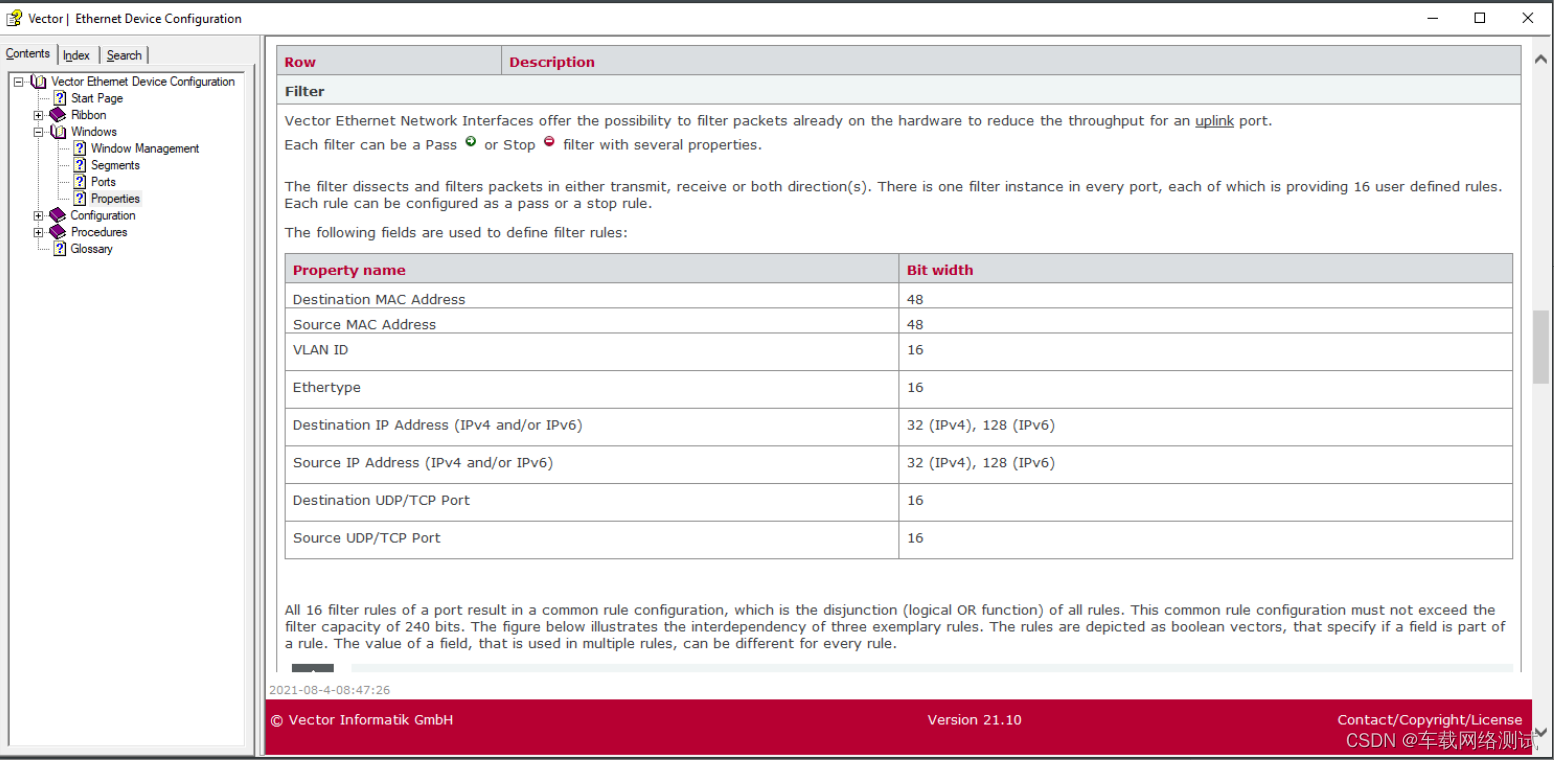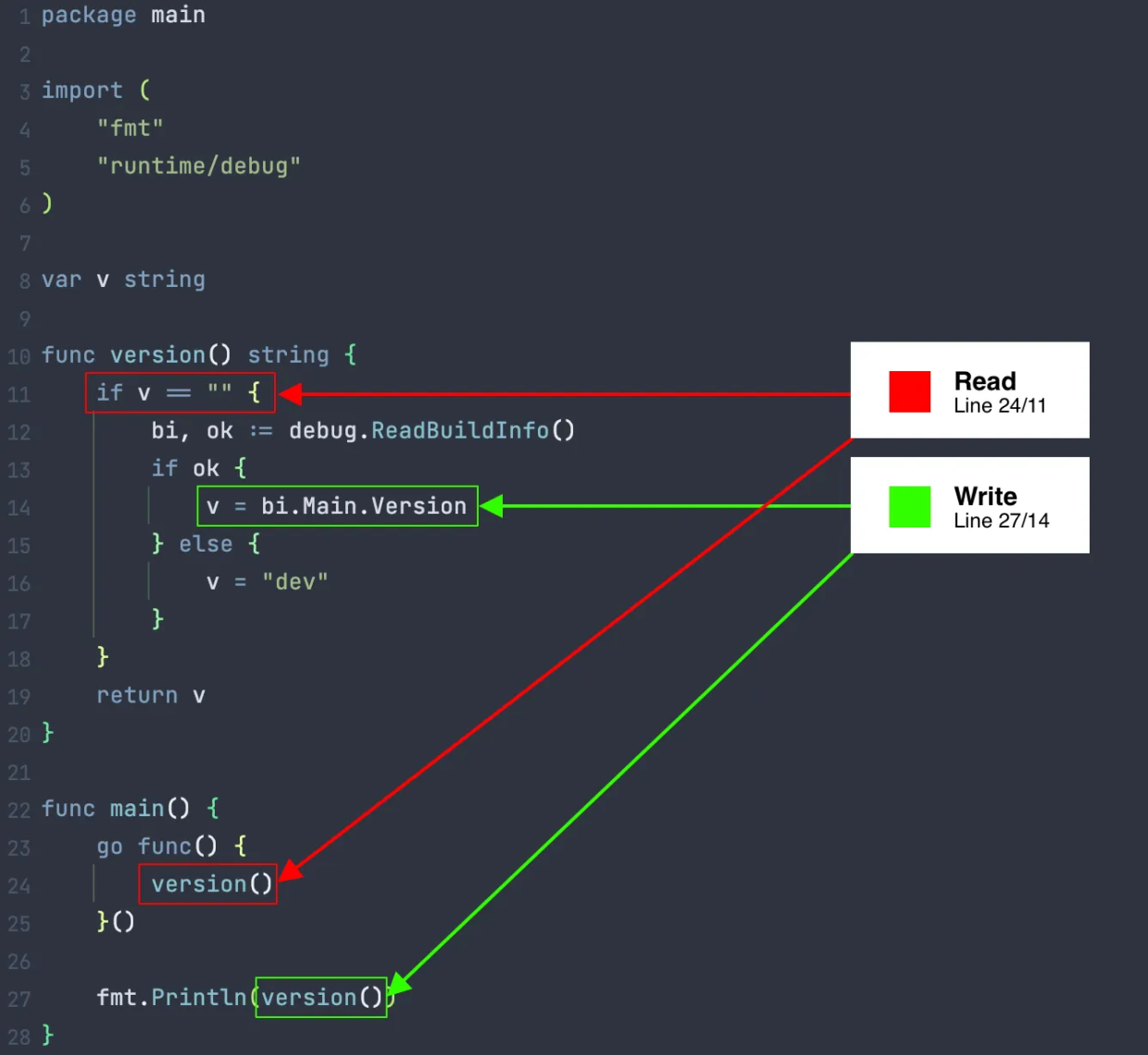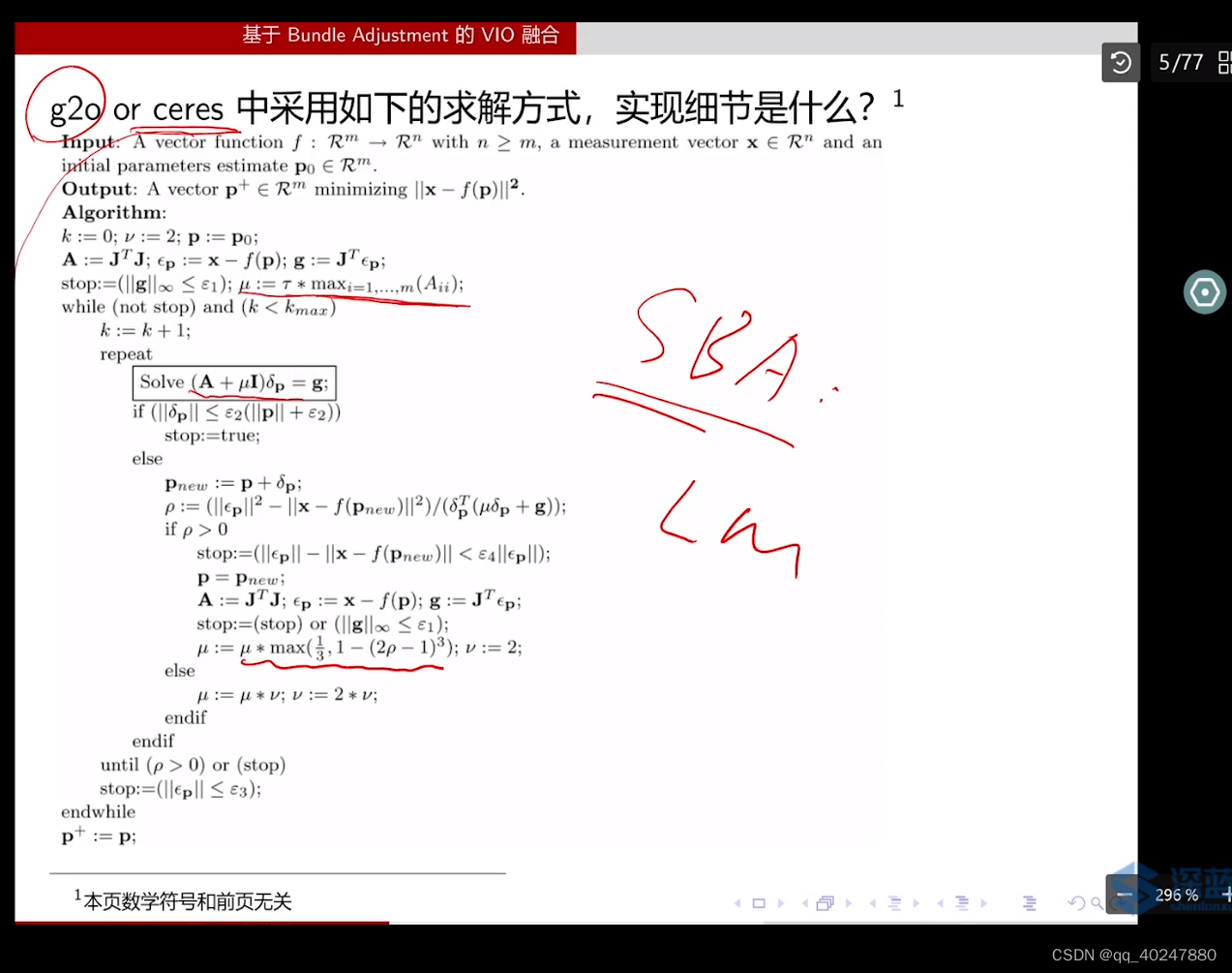
技巧性u初始值,更新的原因都不知道杂来的

F(x)是复杂的非线性函数,所以没法直接求导=0得到最小值。所以展开

两种方法来下降,一种是先找一个方向,在确定一个步长line search。另一种是先确定区域,再找一个点。

J是FX的雅可比已知,d取J反方向就是下降最快的

这里的黑体f(x)是struct后的fx,其对应的J和H和之前的不一样,要叠起来变成矩阵。robust用单个的fx,BA表达用叠在一起的fx粗体
高斯牛顿是fx求雅可比,牛顿是FX求雅可比
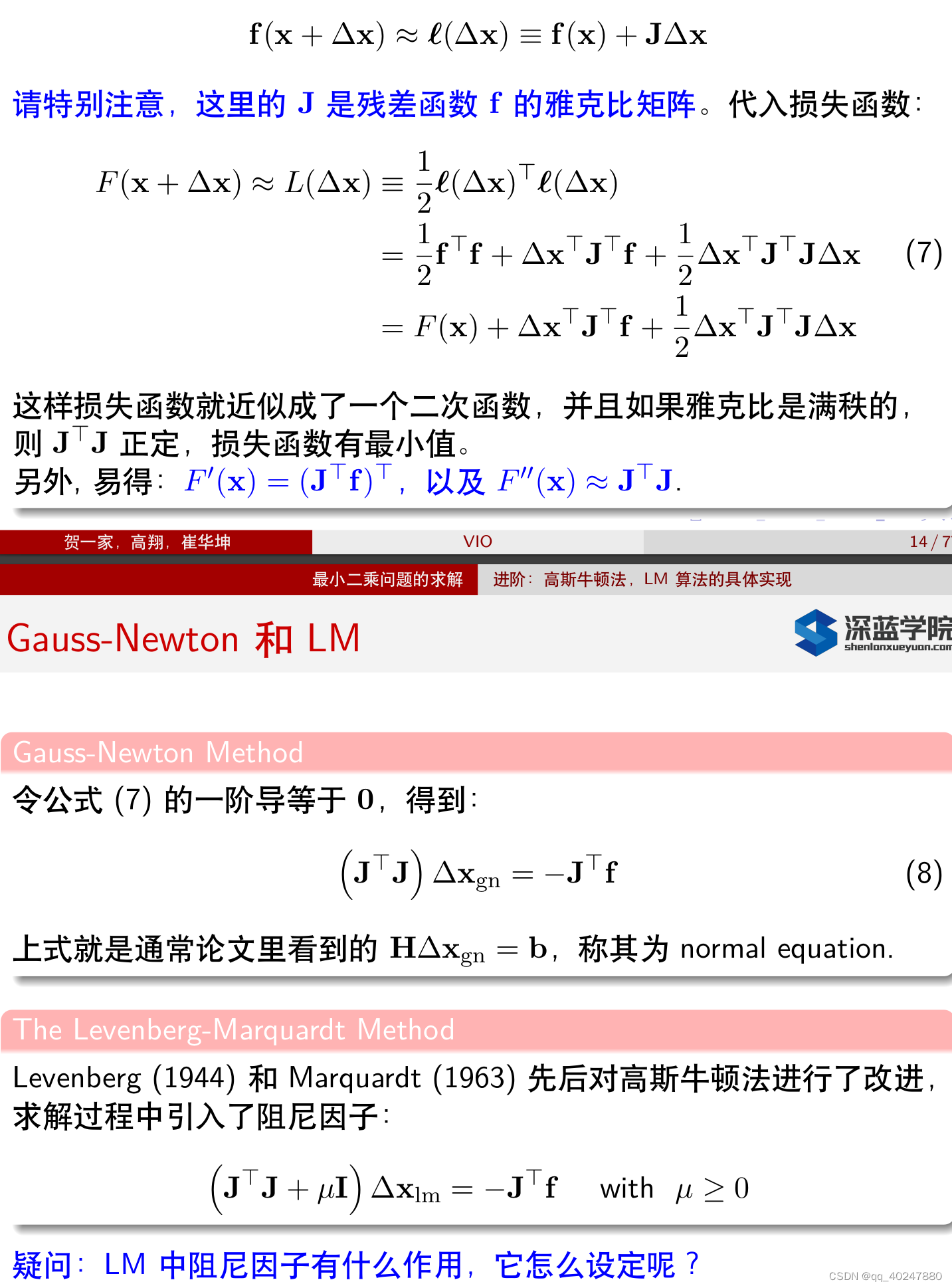
公式8前者是二阶导数H,后者是一阶导数J。u应该别跑太远

svd分解。经验显示u和最大的特征值lamda是同一个数量级,或者JTJ对角线最大值和u同一个数量级,因为不可能每次都去svd分解JTJ。初始值在最优附近,趋向于使用高斯牛顿,所以tao小一点10^-8。
广义韦达定理
矩阵特征值之和等于主对角线元素之和

rou小于0,fx没有下降。分母L-L一直减小,因为步长是根据减少的L的目的实现的

鲁棒核函数=M估计=自适应估计=reweighted

鲁棒和函数等于在JTJ上家了一个权重,huber有参数k算起来简单,cauchy有控制参数c。柯西==IRLS,效果好点,算量大

fx的结果分布方差95%
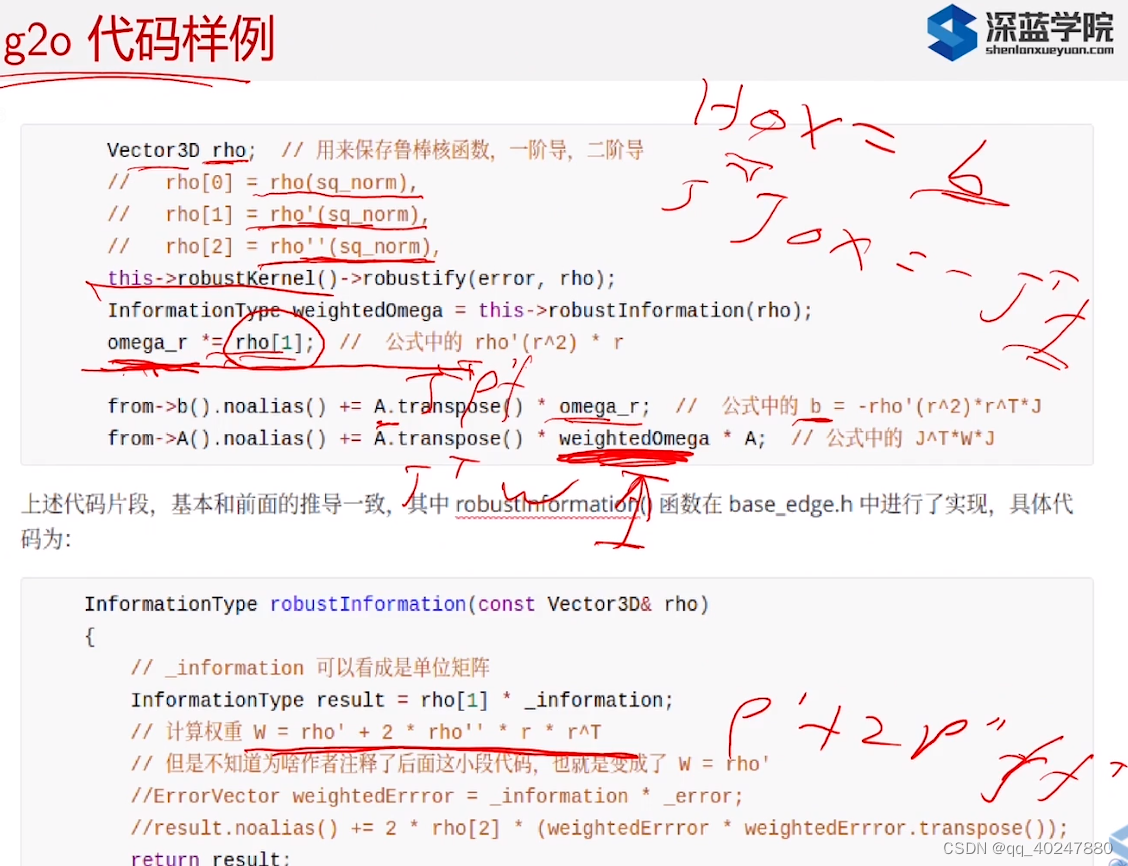
黄色代码和公式17对应
协方差的逆作用:马是距离角度,对不同传感器或者类型误差量(范围)归一化(视觉IMU),权重角度,协方差小,可行度高,他的逆大,权重大

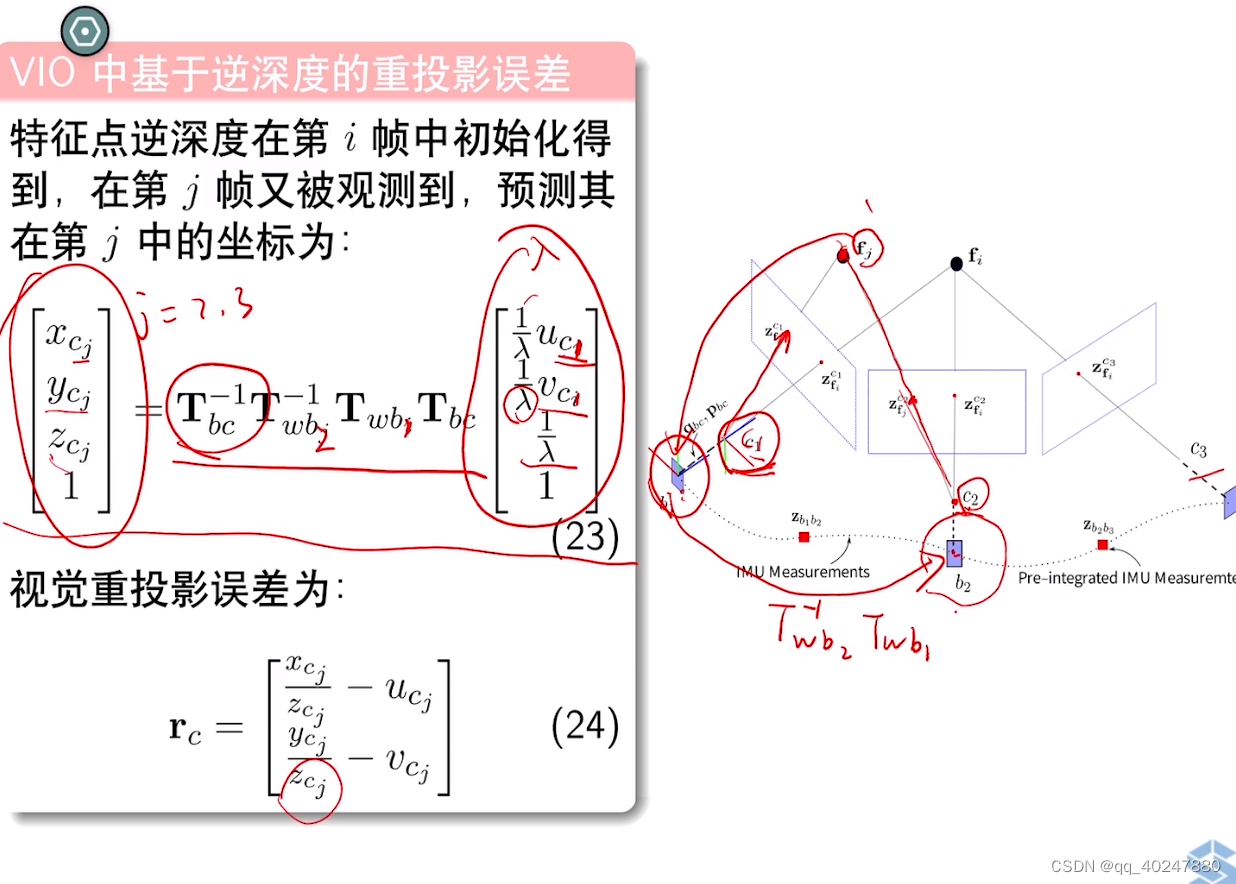
lamda 特征点的逆深度
uv可以认为特别准,唯一自由度为深度,相对于xyz自由度三,逆深度可以省计算量。不用深度用逆深度好处,可以表示无穷远lamda=0,lamda近似高斯分布
纯惯性导航用不到预计分,因为没有优化前一部位资的需要
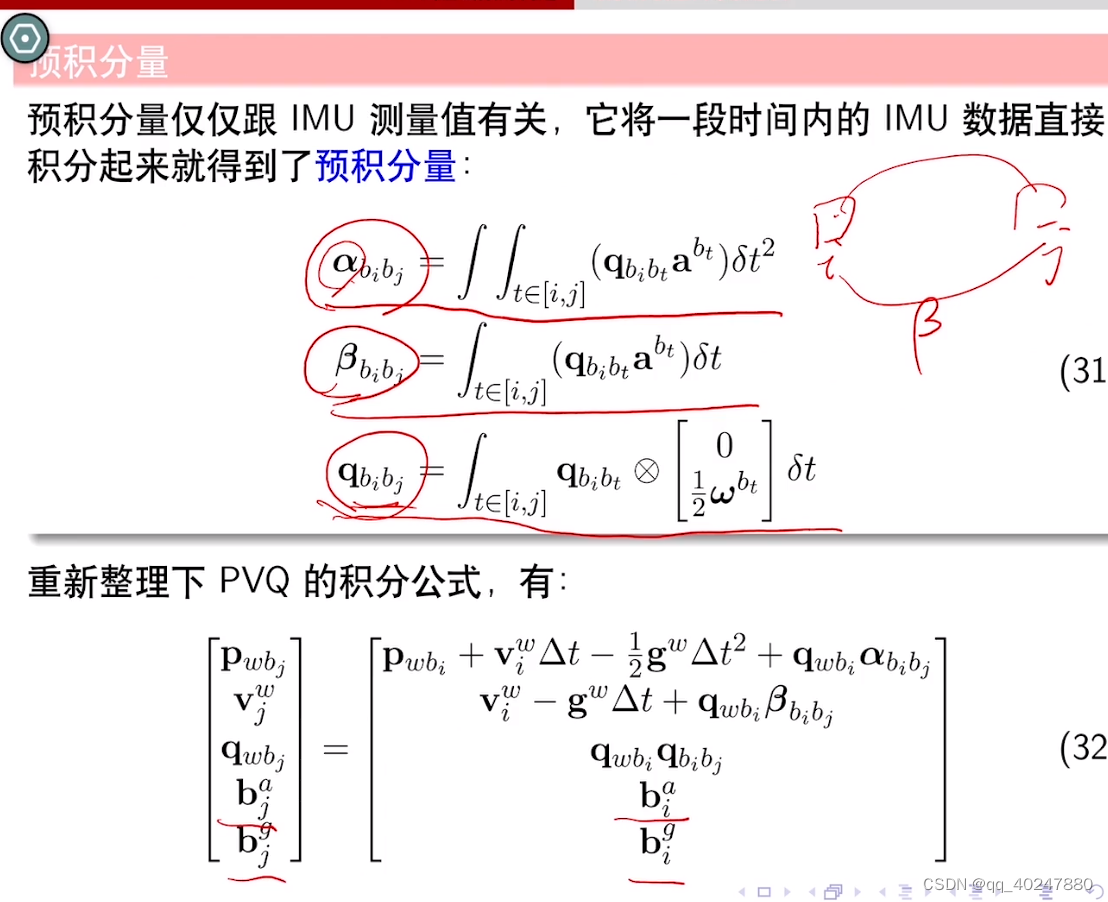
alpha位置变化,beta速度变化,q姿态变化

四元数乘法在小角度时虚部近似为0