【POJ No. 3264】区间最值差 Balanced Lineup

北大OJ 题目地址

其实这道题 之前也做过一次了

http://t.csdn.cn/0YZgC

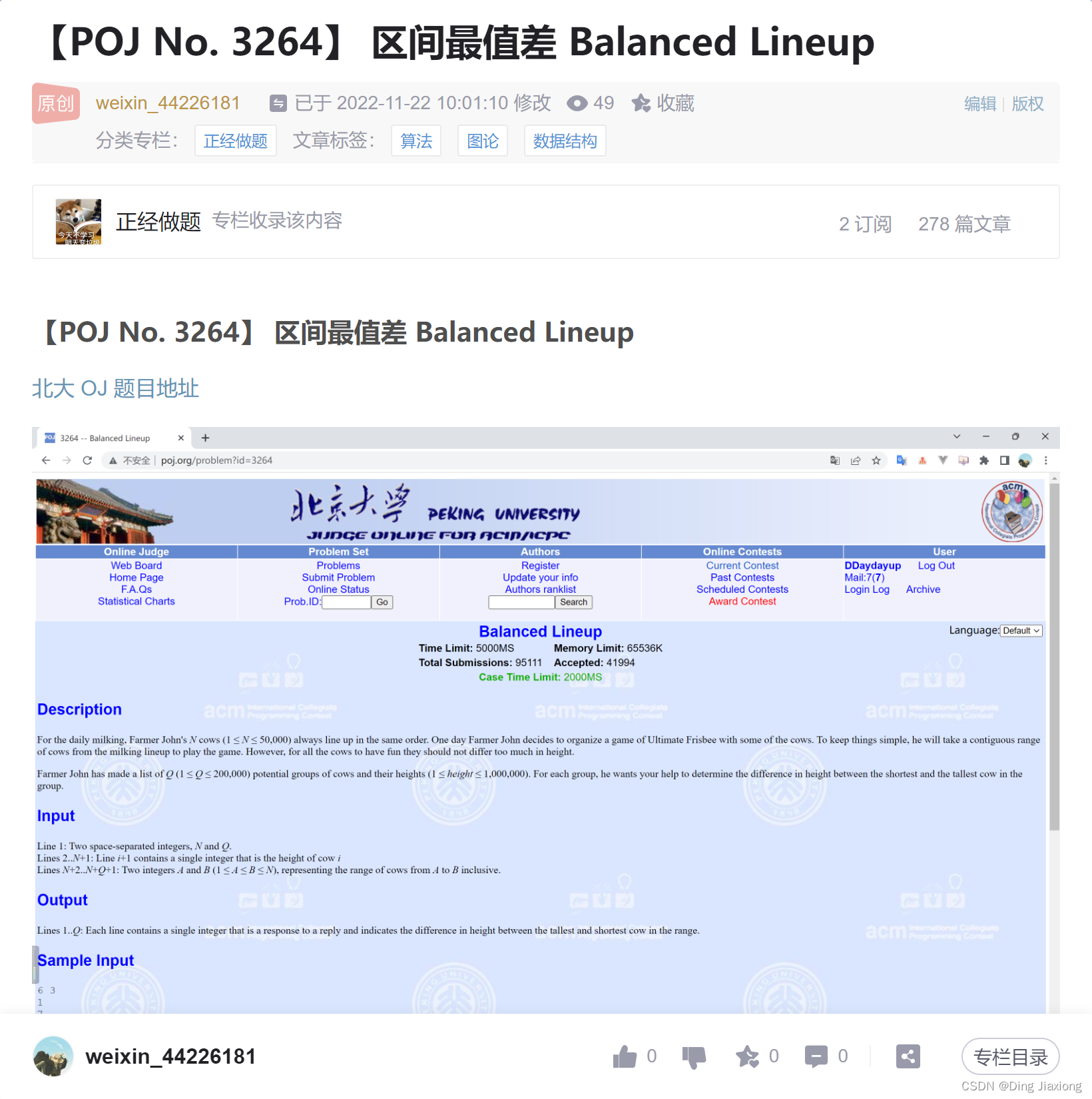
不过上次是用ST 做的。这次换做 分块来实现。

【题意】

每天挤奶时，约翰的N 头奶牛（1≤N≤50,000）都以相同的顺序排队。他挑选一系列连续的奶牛来玩游戏。

为了让所有奶牛都玩得开心，它们的高度差异不应太大。约翰列出了Q组（1≤Q ≤200,000）奶牛和它们的高度（1≤height≤1,000,000）。他希望确定每个小组中最高和最矮的奶牛之间的高度差异。

【输入输出】

输入：

第1行包含两个整数N 和Q 。接下来N 行，每行都包含一个整数，表示奶牛的高度。最后Q 行，每行都包含两个整数A 和B （1≤A≤B ≤N ），代表从A 到B 的奶牛范围。

输出：

输出Q 行，每行都包含一个整数，表示该范围内最高和最矮奶牛的高度差。

【样例】

【思路分析】

这道题是典型的区间最值查询问题，可采用线段树、ST或分块解决。

【算法设计】

① 分块。划分块，记录每个元素所属的块，以及每一块的左右端点下标、最大值和最小值。

② 查询。查询[l , r ]区间最大值和最小值的差值。

• 若该区间属于同一块，则暴力统计最大值和最小值，返回两者的差值。
• 若该区间包含多个块，则统计中间每个块的最大值和最小值，然后暴力统计左端点和右端点的最大值和最小值，返回两者的差值。

【算法实现】

#include<cstdio>
#include<cstring>
#include<algorithm>//max,min
#include<cmath>//sqrt

using namespace std;

const int inf=0x3f3f3f3f;
const int maxn=50010;
int L[maxn],R[maxn],belong[maxn],block_max[maxn],block_min[maxn];
int a[maxn],n,m;

void build(){
    int t=sqrt(n*1.0);
    int num=n/t;
	if(n%num) num++;
    for(int i=1;i<=num;i++)
        L[i]=(i-1)*t+1,R[i]=i*t;
    R[num]=n;
    for(int i=1;i<=n;i++)
        belong[i]=(i-1)/t+1;
    for(int i=1;i<=num;i++){//求每块最值 
    	int MIN=inf,MAX=-inf;
    	for(int j=L[i];j<=R[i];j++){
        	MAX=max(MAX,a[j]);
			MIN=min(MIN,a[j]);		
		}
		block_max[i]=MAX;
		block_min[i]=MIN;	
	}
}

int query(int l,int r){
    int MIN=inf,MAX=-inf;
    if(belong[l]==belong[r]){
        for(int i=l;i<=r;i++){
        	MAX=max(MAX,a[i]);
			MIN=min(MIN,a[i]);	
		}
        return MAX-MIN;
    }
    else{
        for(int i=l;i<=R[belong[l]];i++){//左端
        	MAX=max(MAX,a[i]);
			MIN=min(MIN,a[i]);	
		}
        for(int i=belong[l]+1;i<belong[r];i++){//中间
        	MAX=max(MAX,block_max[i]);
			MIN=min(MIN,block_min[i]);	
		}
        for(int i=L[belong[r]];i<=r;i++){//右端
        	MAX=max(MAX,a[i]);
			MIN=min(MIN,a[i]);	
		}
    }
    return MAX-MIN;
}

int main(){
	
    int l,r;
	while(~scanf("%d%d",&n,&m)){
		for(int i=1;i<=n;i++)//下标从1开始 
			scanf("%d",&a[i]);
		build();
		for(int j=1;j<=m;j++){
			scanf("%d%d",&l,&r);
			printf("%d\n",query(l,r));
		}
	}
	
    return 0;
}