❓18. 四数之和

难度：中等

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

• 0 <= a, b, c, d < n
• a、b、c 和 d 互不相同
• nums[a] + nums[b] + nums[c] + nums[d] == target
• 你可以按 任意顺序 返回答案 。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

提示：

• $1<=nums.length<=200$
• $-10^9<=nums[i]<=10^9$
• $-10^9<=target<=10^9$

💡思路：排序+双指针

• 和 15.三数之和 是一个思路，都是使用双指针法, 基本解法就是在三数之和 的基础上再套一层 for 循环。

🍁代码：(Java、C++)

Java

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> ans = new ArrayList<>();
        Arrays.sort(nums);
        int n = nums.length;
        //极端情况返回空
        if(n < 4 || nums[0] >= 0 && nums[0] > target || nums[n - 1] < 0 && nums[n - 1] < target) return ans;
        for(int i = 0; i < n - 3; i++){
            //剪枝
            if(nums[i] >= 0 && (long)4 * nums[i] > target) break;//对nums[i]去重
            if(i > 0 && nums[i] == nums[i - 1]) continue;

            for(int j = i + 1; j < n - 2; j++){
                //二级剪枝
                if(nums[j] >= 0 && (long)3 * nums[j] + nums[i] > target) break;
                //对nums[i]去重
                if(j > i + 1 && nums[j] == nums[j - 1]) continue;

                int left = j + 1, right = n - 1;
                while(right > left){
                    long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];
                    if(sum < target) left++;
                    else if(sum > target) right--;
                    else{
                        ans.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
                        if(nums[left] == nums[right]) break;//对nums[left]和nums[right]去重
                        while(right > left && nums[left + 1] == nums[left]) left++;
                        left++;
                        while(right > left && nums[right - 1] == nums[right]) right--;
                        right--;
                    }
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> ans;
        sort(nums.begin(), nums.end());
        int n = nums.size();
        //极端情况返回空
        if(n < 4 || nums[0] >= 0 && nums[0] > target || nums[n - 1] < 0 && nums[n - 1] < target) return ans;
        for(int i = 0; i < n - 3; i++){
            //剪枝
            if(nums[i] >= 0 && (long)4 * nums[i] > target) break;
            //对nums[i]去重
            if(i > 0 && nums[i] == nums[i - 1]) continue;

            for(int j = i + 1; j < n - 2; j++){
                //二级剪枝
                if(nums[j] >= 0 && (long)3 * nums[j] + nums[i] > target) break;
                //对nums[i]去重
                if(j > i + 1 && nums[j] == nums[j - 1]) continue;

                int left = j + 1, right = n - 1;
                while(right > left){
                	long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];
                    if(sum < target) left++;
                    else if(sum > target) right--;
                    else{
                        ans.push_back({nums[i], nums[j], nums[left], nums[right]});
                        if(nums[left] == nums[right]) break;//对nums[left]和nums[right]去重
                        while(right > left && nums[left + 1] == nums[left]) left++;
                        left++;
                        while(right > left && nums[right - 1] == nums[right]) right--;
                        right--;
                    }
                }
            }
        }
        return ans;
    }
};

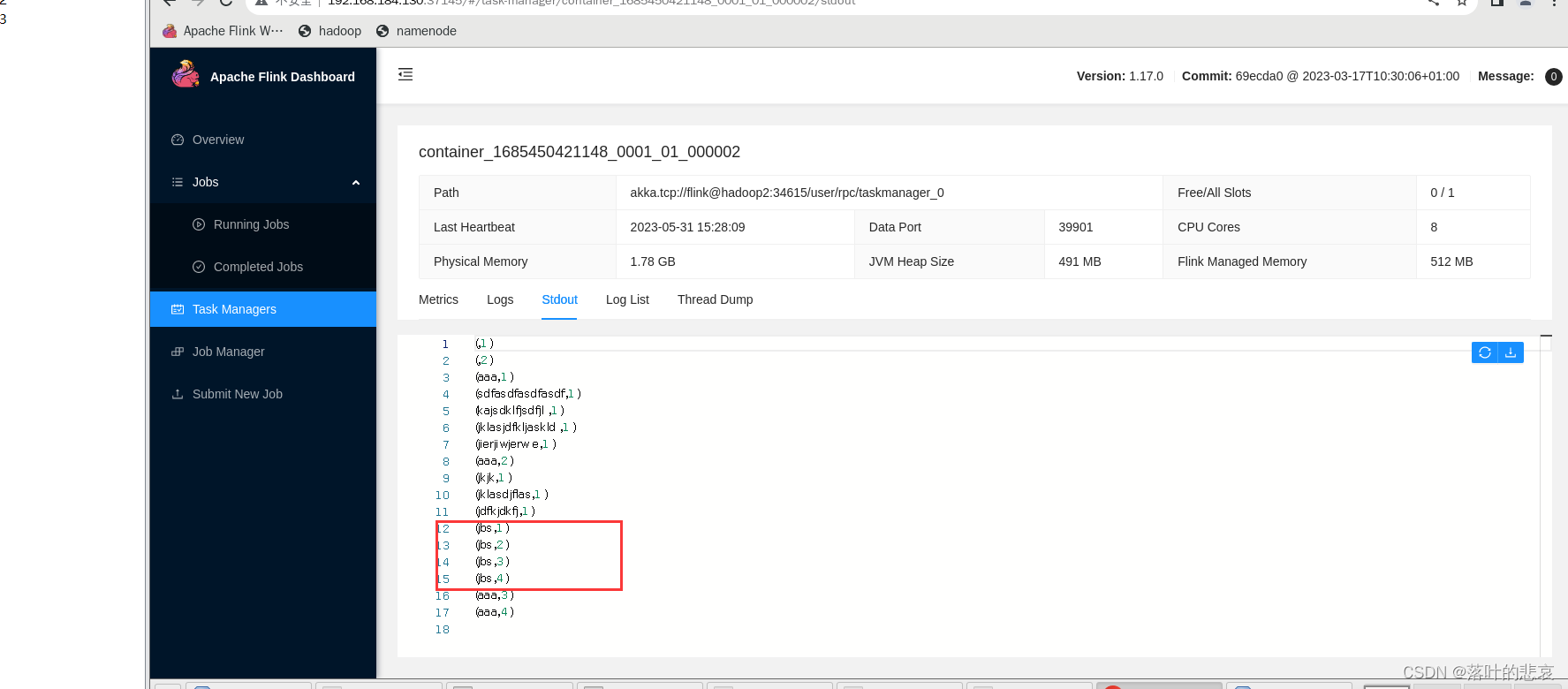
🚀 运行结果：

🕔 复杂度分析：

• 时间复杂度：$O(n^3)$，其中 n 为数组的长度。排序的时间复杂度是 $O(nlogn)$，枚举四元组的时间复杂度是 $O(n^3)$，因此总时间复杂度为 $O(n^3+nlogn)$ = $O(n^3)$。

• 空间复杂度：$O(1)$，忽略存储答案的空间。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我LeetCode主页 / CSDN—力扣专栏，每日更新！

注： 如有不足，欢迎指正！