2022年五一杯数学建模A题
血管机器人的订购与生物学习
原题再现:
随着微机电系统的发展,人类已经可以加工越来越小的机器。这些机器小到一定程度就可以放进血管开展疾病治疗,这就是血管机器人。血管机器人可以携带药物放入血管里定点治疗与血管有关的疾病,还可以充当血管清道夫,清除病毒,保持人体健康。因而,血管机器人越来越受到人们的关注。
血管机器人有多种类型,其中某医院使用的是ABLVR型号的血管机器人。这种血管机器人有两大特点:①可以组装。机器人有一个容器艇(类似于潜艇),有动力,可在血液中游动。容器艇四周安装了4个操作手,操作手类似于人,有生物大脑和机械臂,生物大脑控制着机械臂进行工作。操作手可以从容器艇上拆卸、安装、更换。②需要学习。这种血管机器人没有直接的信息复制功能,新购买的操作手在工作之前需要提前进行生物学习(训练),类似于人脑学习,需要在特定的环境中由已经学习好的操作手(熟练工)“指导”若干个生物大脑芯片空白的操作手(新手)在仿真血管中进行学习,直到“新手”能够达到“熟练工”的水平为止,时间为一周。
血管机器人在患者血管中工作时间是一周,一周后必须取出。取出后操作手拆卸下来需要进行一周的保养才能再次开展工作,如没有安排工作,则一直需要保养。新购买的容器艇需要经过一周的检查调试后才可以投入使用,使用结束后容器艇并不必须要保养,可以连续使用,但如果不使用也需要保养。假定购买的容器艇和操作手在每周开始时到货并立即安排检查调试和生物学习(训练)。相关成本数据见附件1。附件2是第1-104周该医院所需要的血管机器人数量。
该医院从第1周开始开展血管机器人治疗业务,并假定开始前已经有了13个容器艇和50个熟练操作手。请建立数学模型,回答下列问题。
问题1:在每周开始时,医院可以购买到操作手和容器艇。每个熟练操作手可以作为指导者“指导”10个购买的新操作手进行生物学习。如果仅仅考虑第1-8周,请问每周需要购买多少容器艇和操作手,既满足治疗又能够使运营成本达到最低?
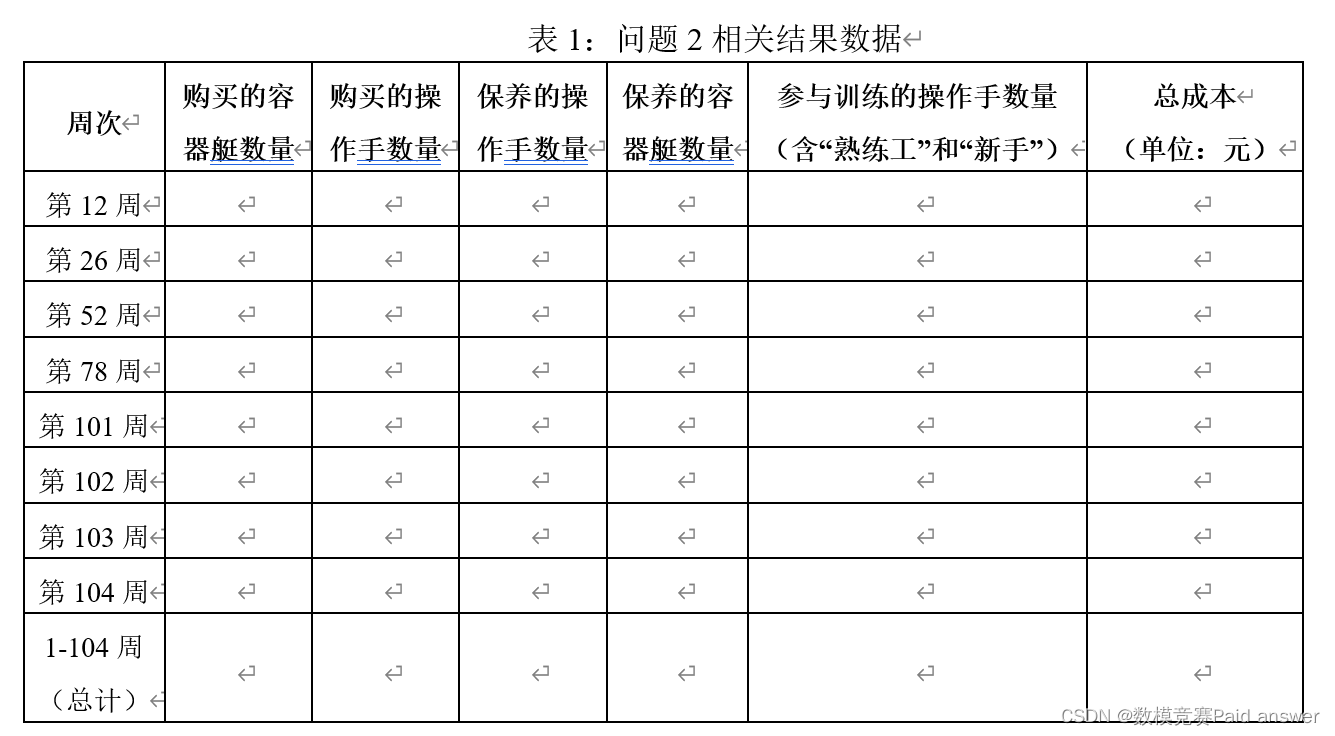
问题2:血管机器人在患者血管中工作有风险,一旦碰上巨噬细胞,如果躲避不及,将会完全损毁。假设每周有20%的血管机器人损毁(损毁的个数按四舍五入取整),其他条件遵循问题1,通盘考虑第1-104周,请问总共需要购买多少容器艇和操作手,既满足治疗又能够使运营成本达到最低?并将相关结果填入表1。另外,将第1-8周的结果数据与问题1的第1-8周的结果数据进行对比分析。
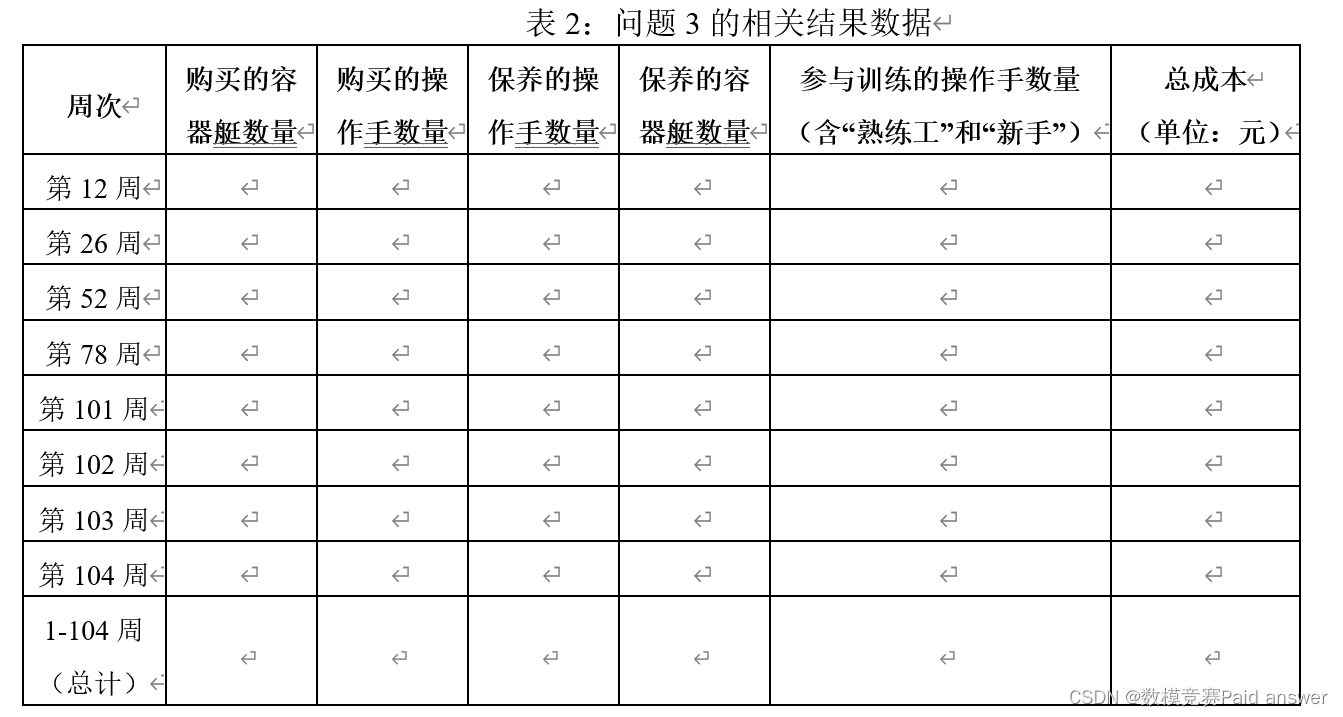
问题3:如果每名熟练操作手可以“指导”新操作手的数量调整为不超过20个,假设每周有10%的血管机器人损毁(损毁的个数按四舍五入取整),同问题2,请研究第1-104周里总共需要购买多少容器艇和操作手既满足治疗又能够使运营成本达到最低?将相关结果数据填入表2。
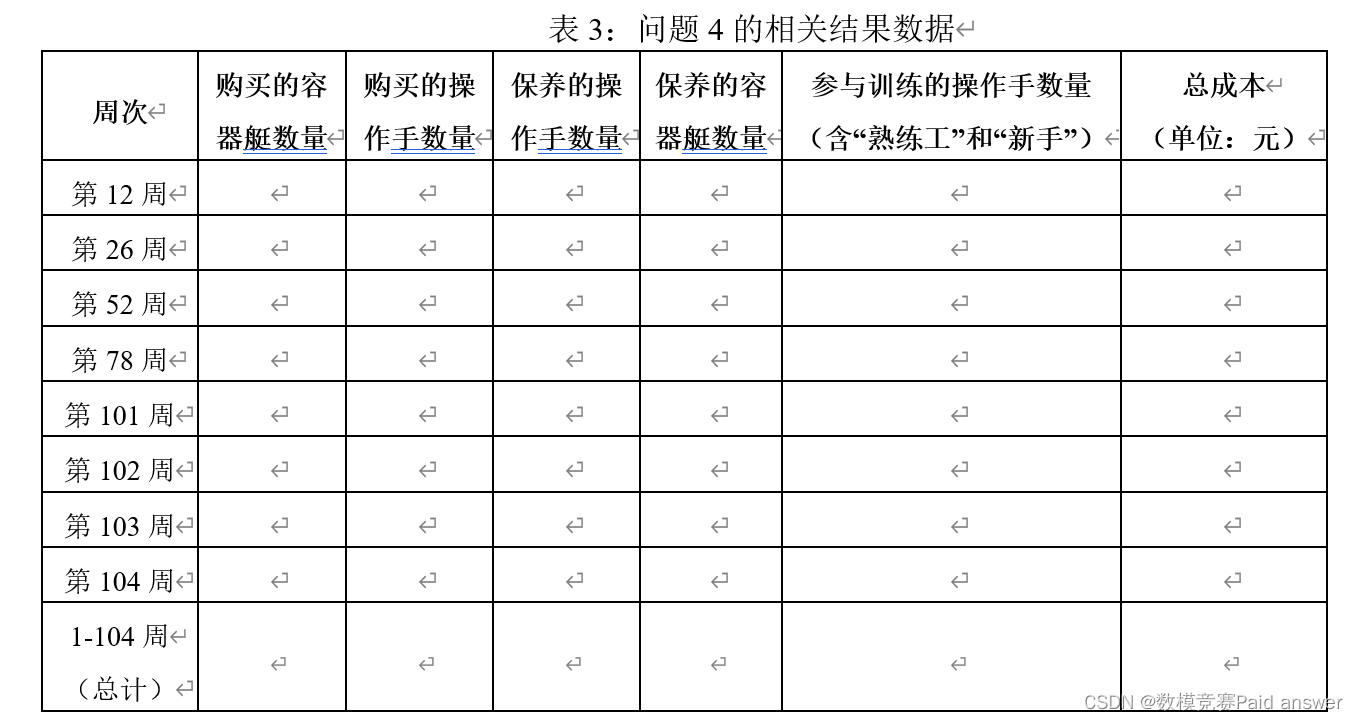
问题4:如果购买操作手和容器艇有优惠政策,即容器艇一次性购买量不超过5个时的单价为200元/个;容器艇一次性购买量超过5个但不超过10个时,超过5个的那部分单价为180元/个;容器艇一次性购买量超过10个时,超过10个的那部分单价为160元/个。同样,操作手一次性购买量不超过20个时的单价为100元/个;操作手一次性购买量超过20个但不超过40个时,超过20个的那部分单价为90元/个;操作手一次性购买量超过40个时,超过40个的那部分单价为80元/个。其他条件遵循问题3,则第1-104周里总共购买的容器艇和操作手将如何调整?将相关结果数据填入表3。
问题5:预测第105-112周的血管机器人的使用需求。为了研究第105-112周的血管机器人的使用成本,在遵循问题4条件的基础上,有两种方案可以考虑。
方案1:在第1-104周最优结果的基础上,医院在第105周开始时有可能需要以每个300元的高价购买能够直接使用的容器艇和每个150元购买熟练操作手,而后续每周均按问题4中的优惠政策购买合适数量的新容器艇和新操作手,满足第105-112周的血管机器人的需求。
方案2:通盘考虑第1-112周的血管机器人的需求。
请比较两种方案的第1-112周最低运营成本的差额。
整体求解过程概述(摘要)
近年来,在科技蓬勃发展的同时,不规律的生活习惯使越来越多的人们被心脑血管疾病所困扰。而血管机器人可以携带药物放入血管里定点治疗与血管有关的疾病,还可以充当血管清道夫,清除病毒,保持人体健康。因而,血管机器人越来越受到人们的关注。
对于问题一,要求我们规划求解出每周需要购买多少容器艇和操作手,可以既满足治疗又能够使运营成本达到最低。不难看出这是一个规划问题,可用优化算法求解,但由于后面周的采集量受到下一周需求量和当期存量的影响,不知道后面周的参数范围,因此需要通过仿真模拟实验来进行寻优。
对于问题二,仍是寻求需要购买多少容器艇和操作手,但在第一问基础上,需要考虑损毁,损毁就会增加需求和成本。与此同时,还要通盘考虑考虑第 1-104周。在此首先还是确定每周容器艇和操作手的购买数量范围,然后进行寻优。
对于问题三,相比于上一问只是指导数量增加,对应血管机器人损毁数量减少其他条件与上一问相同,研究求解时只需注意用新的条件替换原来的条件即可。
对于问题四,大体条件与上一问相同,只是在购买操作手和容器艇的方面增加了优惠政策,在此条件下分析购买的容器艇和操作手改如何调整。本问主要涉及到成本问题,故在第 3 问基础上增加计算成本条件,进行寻优。
对于问题五,需要我们预测第 105-112 周的血管机器人的使用需求,同时考虑到血管机器人的使用成本,通过分析比较两种方案的第 1-112 周最低运营成本的差额。在此可以选用时间序列预测法,得到结果为-132390。
问题背景
随着微机电系统的发展,人类已经可以研制出血管机器人,它可以携带药物放入血管里定点治疗与血管有关的疾病,还可以充当血管清道夫,清除病毒,使其越来越受到人们的关注。国内高校实验室、研究院提出新型血管螺旋式微型机器人"的各项研究技术,如基于外磁场驱动的研究3,不同血管条件下外流场对比分析3等,丰富了血管机器人领域的知识,为之后的研究提供支持;国外同样进行相似的研究并投入使用如Corindus 血管机器人,自2016年起财务结果收入不断攀升阉,并预测全球机器人飞行模拟器手术市场2027主要关键人物就有Corindus 血管机器人[5]。
人类也因此研发出不同类型的血管机器人,拥有不同的特点和功能,如 ABLVR型号的血管机器人,这种血管机器人有两大特点:①可以组装。机器人有一个容器艇(类似于潜艇),有动力,可在血液中游动。容器艇四周安装了4个操作手,操作手类似于人,有生物大脑和机械臂,生物大脑控制着机械臂进行工作。操作手可以从容器艇上拆卸、安装、更换。②需要学习。这种血管机器人没有直接的信息复制功能,新购买的操作手在工作之前需要提前进行生物学习(训练),类似于人脑学习,需要在特定的环境中由已经学习好的操作手(熟练工)“指导”若干个生物大脑芯片空白的操作手(新手)在仿真血管中进行学习,直到“新手”能够达到“熟练工”的水平为止,时间为一周,而工作一周后必须取出拆卸保养一周之后再开展工作。而医院从第1周开始开展血管机器人治疗业务,并假定开始前已经有了13个容器艇和50个熟练操作手。
问题重述
本文通过建立数学模型,解决以下问题:
1.每个熟练操作手可以作为指导者“指导”10个购买的新操作手进行生物学习。若只学习8周,请问医院每周开始需要购买多少容器艇和操作手,既满足治疗又能够使运营成本达到最低?
2.巨噬细胞可使在患者血管中工作的血管机器人完全损毁。在问题一的背景下并假设每周有20%的血管机器人损毁(损毁的个数按四舍五入取整),通盘考虑第1-104周,请问医院总共需要购买多少容器艇和操作手,既满足治疗又能够使运营成本达到最低?并将相关结果填入表1。并对问题一和问题二的第1-8周的结果数据进行对比分析得结果;
3.每名熟练操作手的精力有限,若每名熟练操作手可以“指导”新操作手的数量调整为不超过20个,假设每周有10%的血管机器人损毁(损毁的个数按四舍五入取整),请研究第1-104周里总共需要购买多少容器艇和操作手,既满足治疗又能够使运营成本达到最低﹖将相关结果数据填入表2;
4.如果购买操作手和容器艇有优惠政策,即容器艇一次性购买量不超过5个时的容器艇单价为200元/个;容器艇一次性购买量超过5个但少于10个时,超过5个的那部分容器艇单价为180元/个;容器艇一次性购买量超过10个时,超过10个的那部分单价容器艇为160元/个。同样,操作手一次性购买量不超过20个时的操作手单价为100元/个;操作手一次性购买量超过20个但少于40个时,超过20个的那部分操作手单价为90元/个;操作手一次性购买量超过40个时,超过40个的那部分操作手单价为80元/个。在问题三的条件下,则第1-104周里总共购买的容器艇和操作手将如何调整?将相关结果数据填入表3;
5.医院需要预测第105-112周的血管机器人的使用需求,为了研究第105-112 周的血管机器人的使用成本,在问题四的条件基础上,有两种方案可以考虑。方案1:在第1-104周最优结果的基础上,医院在第105 周开始时有可能需要以每个300元的高价购买能够直接使用的容器艇和每个150元购买熟练操作手,而后续每周均按问题4中的优惠政策购买合适数量的新容器艇和新操作手,可满足第105-112周的血管机器人的需求。方案2:通盘考虑第1-112周的血管机器人的需求。请比较两种方案的第1-112周最低运营成本的差额。
模型的假设:
结合本题的实际,为确保模型求解的准确性和合理性,本文排除–些因素的干扰,
提出以下几点假设:
1.假设所购买的容器艇和操作手均无质量问题;
2.假设保养后的血管机器人有如同全新血管机器人一样的工作效率;
3.假设除购买、保养容器艇和购买、保养及训练操作手外无其他花费。
问题分析
问题 1 的分析
在每周开始时,医院会购买到操作手和容器艇。而每个熟练操作手可以作为指导者“指导”1 新操作手进行学习。现要求我们规划求解出每周需要购买多少容器艇和操作手,可以既满足治疗又能够使运营成本达到最低。不难看出这是一个规划问题,可用优化算法求解,但由于后面周的采集量受到下一周需求量和当期存量的影响,不知道后面周的参数范围,因此不能当作寻常的优化问题来看,而是需要通过仿真模拟实验来进行寻优。
问题 2 的分析
与第一问大体相同,仍是寻求需要购买多少容器艇和操作手,才可以既满足治疗又能够使运营成本达到最低。但在第一问基础上,需要考虑损毁,损毁就会增加需求和成本。与此同时,还要通盘考虑考虑第 1-104 周。在此首先还是确定每周容器艇和操作手的购买数量范围,然后进行寻优。
问题 3 的分析
现规定每名熟练操作手可以“指导”新操作手的数量调整为不超过 20 个,假设每周有 10%的血管机器人损毁,其他条件与上一问相同,研究第 1-104 周里总共需要购买多少容器艇和操作手。由题可看出相比于上一问只是指导数量增加,对应血管机器人损毁数量减少。求解时只需注意用新的条件替换原来的条件即可。
问题 4 的分析
本问大体条件与上一问相同,只是在购买操作手和容器艇的方面增加了优惠政策,在此条件下分析第 1-104 周里总共购买的容器艇和操作手改如何调整。本问主要涉及到成本问题,故在第 3 问基础上增加计算成本条件,进行寻优。
问题 5 的分析
本问需要我们预测第 105-112 周的血管机器人的使用需求,同时考虑到血管机器人的使用成本,在遵循问题 4 条件的基础上,给出了两种方案,通过计算分析比较两种方案的第 1-112 周最低运营成本的差额。在此可以选用时间序列预测法,在第四问的基础上增加条件进行寻优。
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分代码:
clear
clc
%由于后面周的采集量受到下一周需求量和当期存量的影响,不知道后面周的参数范围
%因此不能当作寻常的优化问题来看,因此只能做仿真模拟实验
%这样也能很大程度提高寻优效率,最后的结果只能是尽可能最优,很难达到真正的最优
T=100; %初始化温度值
T_min=1; %设置温度下界
alpha=0.95; %温度的下降率
num=1000; %颗粒总数
XQ=[11,5,4,7,16,6,5,7,13,6];%各周需求
p=4;%容器艇配备的机械手数
L=10;%一个指导机械手可训练新操作手的数目
Y=zeros(9,length(XQ));%记录过程数据
Y(:,1)=[0
13
50
0
0
0
0
0
0];%操作手数
G=[200
100
5
10
10];%容器艇\操作手\操作手保养\容器艇保养\操作手训练成本
X1=[];
F1=[];
for i=1:num
for j=1:num
else
pp=ex
if pp>rand
F1(j,1)=FF1(j,1);
X1{j,:}=
end
if min(F1)
[bestf,b]=min(F1);
besty=X1{b,1};
end
ylabel('总成本')
function [X1,F1]=fun_%YY 矩阵每行:第一周使用的机器人\剩余容器艇\剩余操作手\保养容器
艇\保养操作手\指导操作手\训练操作手\购买容器艇数\购买操作手数
flag=0;
while flag==0
YY=Y;
xq=XQ(j);%本周周机器人需求量
要保养,下一周可用容器艇数
YY(5,j+1)=YY(5,j+1)+YY(1,j)*p;
YY(3,j+2)=YY(3,j+2)+YY(1,j)*p;
xq1=XQ(j+1);%下一周机器人需求量
xq2=XQ(j+2);%下下一周机器人需求量
%如果
k1=max(xq1-YY(2,j+1),xq2-YY(2,j+2));
if k1<0
k1=0;
end
%剩余未用来训练的机械手+用于指导的机械手+培养的机械手应当满足下一周需
求,同理也应满足第三周需求量
k2=xq1*p-YY(5,j);
if k2<0
%确定当周至少要购买的机械手数
k2=k2+kk2;
%最大采购则是上一周剩余的机械手数*L
k3=min(k2+10,YY(5,j)*L);%但是也不能过高
if k3<k2
k3=k2;
end
%也不能就 k2,因为可能后面会有突发的需求,采购当期最大训练数也满足不了
%购买容器艇数
%购买机械手数练和保养
)+gm1;
YY(2,j+1)=m2/L);
YY(6,j)=YY(6,j)+ceil(gm2/L);
%下一周剩余操作手
YY(3,j+1)=YY(3,j+1)+YY(7,j)+YY(8,j);
%记录购买数量
YY(8,j)=gm1;
YY(9,j)=gm2;
if length(find(YY<0))==0
end
%计算成本
F1=sum(sum(YY([8,9,5,4,7],1:8).*G));