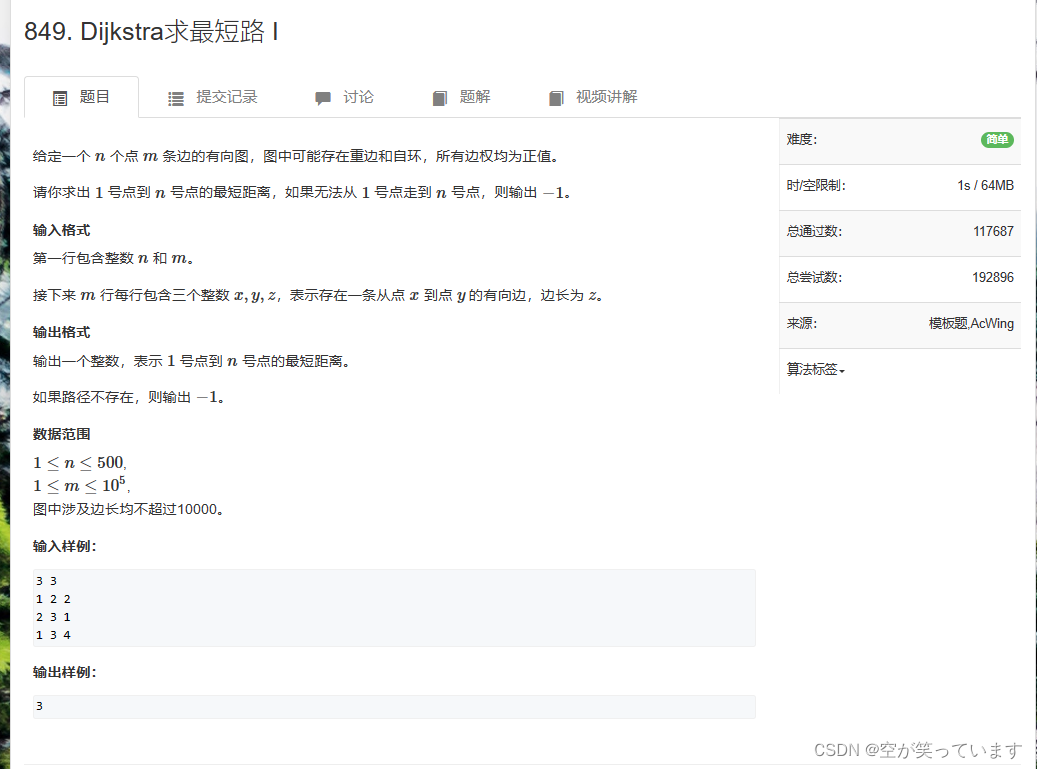
Dijkstra求最短路

我们先来说说这道算法的过程：

和上道题不同的是我们这次是求一个有向图到最终节点的最短距离，所以其策略也有所不同。我们先手动模拟一下过程吧假如有4个点，有他们之间有五条边，那么我们如何来求其1到4的最短路径呢？

1.首先看下图，我们有1到4 4个节点 其中五条边在右边

 

 2.先从1开始初始化，从1出发的有两条变，最短路径图就变成这样了

3.然后因为离3近，所以跳到3开始初始化最短路径图。然后我们发现已经有一条通往4的路了，但是不一定是最好的所以我们需要继续遍历 

4.然后继续遍历我们发现上面那一条就是最短的。

 当遍历到2的时候，我们发现多了两条可以达到4的边，但是其距离都比原先那条远，所以最终还是走那一条就行了。

 题目解题思路

就是模拟上面的过程

1.找到现在离此时的出发点最近的点

    int t = -1;
        //遍历每个节点
        //用vis来控制是否初始化过这个节点
        for(int j=1;j<=n;j++){
            if(!vis[j]&&(t==-1||dist[t]>dist[j])){
                t = j;
            }
        }
        vis[t] = true;

2.然后开始遍历它旁边的节点，更新其他节点到其的距离。为下一次计算最近的点做初始化准备

        for(int j=1;j<=n;j++){
            dist[j] = min(dist[j],g[t][j] + dist[t]);
            // cout<<"t:"<<t<<"j:"<<j<<" "<<dist[j]<<" ";
        }

3.当把所有的节点都初始化完之后，我们也就得出了1到n最短的距离

int Dijkstra(){
    //选择节点1为开始节点，并初始化各个节点之间的距离
    memset(dist,0x3f,sizeof(dist));
    //先给初始点的距离化为0，从它出发肯定是0.
    dist[1] = 0;
    for(int i=0;i<n;i++){
        int t = -1;
        //遍历每个节点
        //用vis来控制是否初始化过这个节点
        for(int j=1;j<=n;j++){
            if(!vis[j]&&(t==-1||dist[t]>dist[j])){
                t = j;
            }
        }
        vis[t] = true;
        for(int j=1;j<=n;j++){
            dist[j] = min(dist[j],g[t][j] + dist[t]);
            // cout<<"t:"<<t<<"j:"<<j<<" "<<dist[j]<<" ";
        }
        // cout<<endl;
    }
    return dist[n];
}

AC代码 

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 510;
int n,m;
int g[N][N];
int dist[N];
bool vis[N];

int Dijkstra(){
    //选择节点1为开始节点，并初始化各个节点之间的距离
    memset(dist,0x3f,sizeof(dist));
    //先给初始点的距离化为0，从它出发肯定是0.
    dist[1] = 0;
    for(int i=0;i<n;i++){
        int t = -1;
        //遍历每个节点
        //用vis来控制是否初始化过这个节点
        for(int j=1;j<=n;j++){
            if(!vis[j]&&(t==-1||dist[t]>dist[j])){
                t = j;
            }
        }
        vis[t] = true;
        for(int j=1;j<=n;j++){
            dist[j] = min(dist[j],g[t][j] + dist[t]);
            // cout<<"t:"<<t<<"j:"<<j<<" "<<dist[j]<<" ";
        }
        // cout<<endl;
    }
    return dist[n];
}

int main(){
    cin>>n>>m;
    memset(g,0x3f,sizeof(g));
    while(m--){
        int a,b,c;
        cin>>a>>b>>c;
        g[a][b] = min(g[a][b],c);
    }
    int res = Dijkstra();
    if(res == INF) cout<<"-1";
    else{
        cout<<res;
    }
    return 0;
}