一、题目
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity)以 正整数 作为容量capacity初始化LRU缓存int get(int key)如果关键字key存在于缓存中,则返回关键字的值,否则返回-1。void put(int key, int value)如果关键字key已经存在,则变更其数据值value;如果不存在,则向缓存中插入该组key-value。如果插入操作导致关键字数量超过capacity,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
二、示例
2.1> 示例:
【输入】
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
【输出】
[null, null, null, 1, null, -1, null, -1, 3, 4]
【解释】
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
提示:
1<= capacity <=30000<= key <=100000<= value <=10^5- 最多调用
2 * 10^5次get和put
三、解题思路
根据题目描述,我们需要构造一个LRU缓存,那么我们需要解决两个问题:
【问题1】实现对
key和value的数据进行缓存。
【问题2】实现LRU的能力,即:最近最少使用。
那么针对第一个问题,我们可以采用哈希表或者数组的方式进行数据存储,因为本题的提示部分已经指出key值是在[0, 10000]区间内的,并不存在负数,所以为了提升执行速度,我们选择数组作为底层的存储结构。其中,需要注意的是,存储的value是下面要介绍的双向链表中的Node节点。
那么针对第二个问题,我们可以采用双向链表的方式进行支持,那么为什么是双向链表呢?因为当调用lRUCache.get()或lRUCache.set()方法对某个Node进行操作的时候,我们需要将这个Node放到链表的尾部,这样,就需要操作该Node节点的前置节点和后置节点,为了便于这种操作,所以我们采用双向链表。执行步骤如下所示:
【步骤1】断开
PreNode与Node的链接关系;
【步骤2】断开NextNode与Node的链接关系;
【步骤3】链接PreNode与NextNode;
【步骤4】将Node放到链表尾部;
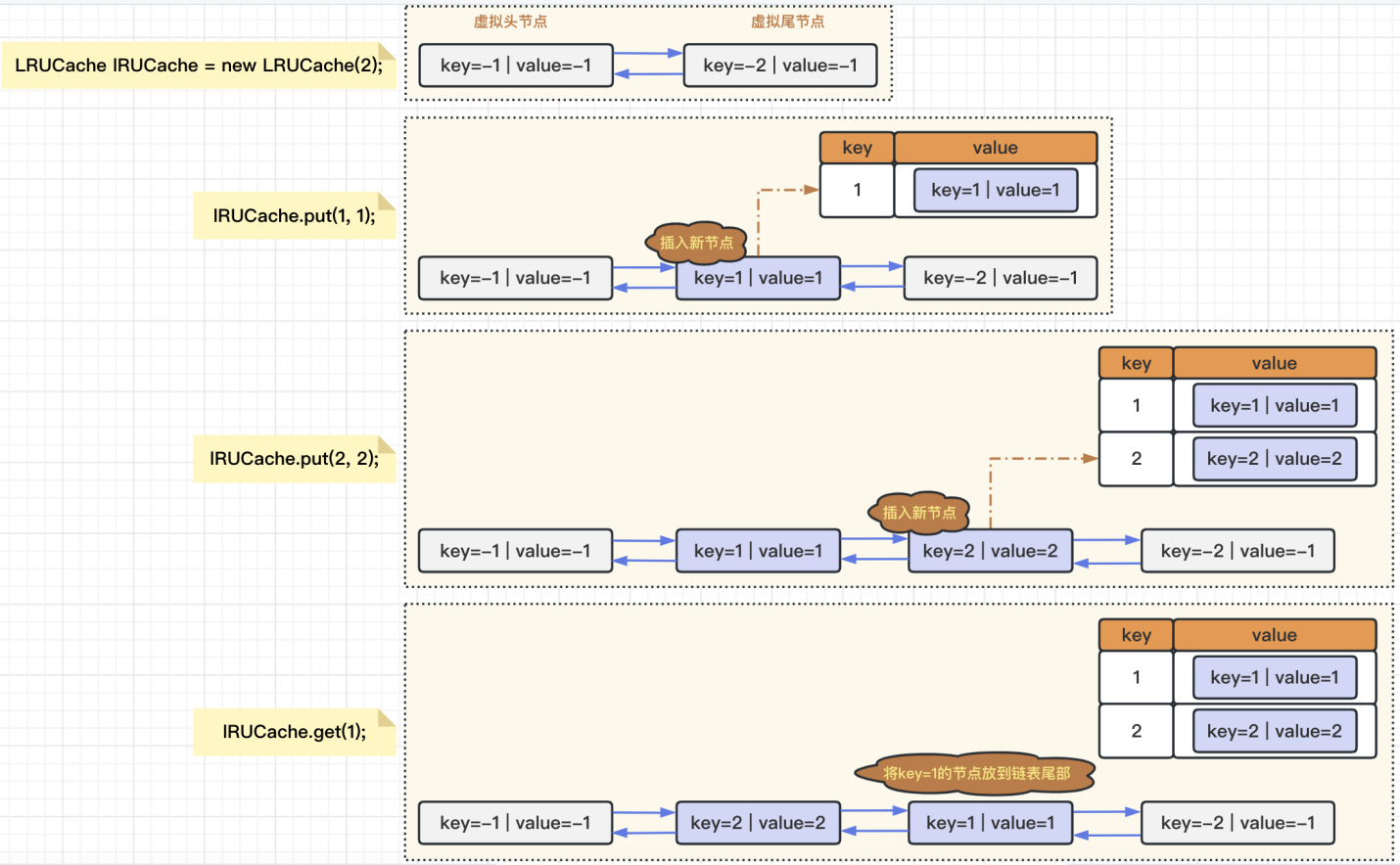
那么这里还有一个小细节,就是如果待移动的节点在头节点,那么我们还需要进行特殊的判断(因为头节点没有前置节点PreNode),而同样的,如果待删除的节点是尾节点,那么我们也需要进行特殊的判断(因为尾节点没有后置节点NextNode)。为了统一处理逻辑,我们可以通过创建虚拟的头尾节点来解决这个问题,即:
【虚拟头节点】Node
head= new Node(-1, -1);
【虚拟尾节点】Nodetail= new Node(-2, -1);
【初始情况下】head.next= tail;tail.pre= head;
由于我们可以知道LRU链表容量的,所以当超出这个容量的时候,就将整个链表中,第一个节点删除即可(不包含虚拟收尾节点),并将哈希表/数组中相应key对应的value置为null;以上就是这道题的解题思路,为了便于大家理解,我们通过创建2节点容量的LRU,具体看一下具体的处理过程,请见下图所示:

四、代码实现
class LRUCache {
Node[] hashTable; // 哈希表
int capacity = 0, count = 0;
Node head, tail;
public LRUCache(int capacity) {
this.capacity = capacity;
hashTable = new Node[10001];
head = new Node(-1, -1); // 虚拟头节点
tail = new Node(-2, -1); // 虚拟尾节点
head.next = tail;
tail.pre = head;
}
public int get(int key) {
Node node;
if ((node = hashTable[key]) == null) return -1; // 如果不存在,直接返回-1
moveNode(node); // 将node节点移动到末尾(位置是tail节点的pre节点)
return node.value;
}
public void put(int key, int value) {
Node node;
if ((node = hashTable[key]) != null) { // 已存在节点,直接修改value值
node.value = value;
} else { // 不存在节点,则新建Node
if (count < capacity) { // 没有到达容量上限
count++;
} else { // 超出容量上限,则需要删除“最近最少使用”的节点
hashTable[head.next.key] = null;
delNode(head.next);
}
node = new Node(key, value);
hashTable[key] = node;
}
moveNode(node); // 将node节点移动到末尾
}
// 删除节点操作
public void delNode(Node node) {
if (node.pre == null || node.next == null) return;
node.pre.next = node.next;
node.next.pre = node.pre;
}
// 将节点移动到“末尾”操作(位置是tail节点的pre节点)
public void moveNode(Node node) {
if (tail.pre == node) return; // 如果已经是“末尾”节点,则不操作
delNode(node); // 删除该节点的前后关联,下面会进行重新关联操作
tail.pre.next = node;
node.pre = tail.pre;
node.next = tail;
tail.pre = node;
}
// 双向链表结构
class Node {
public int key, value;
public Node pre, next;
public Node(int key, int value) {
this.key = key;
this.value = value;
}
}
}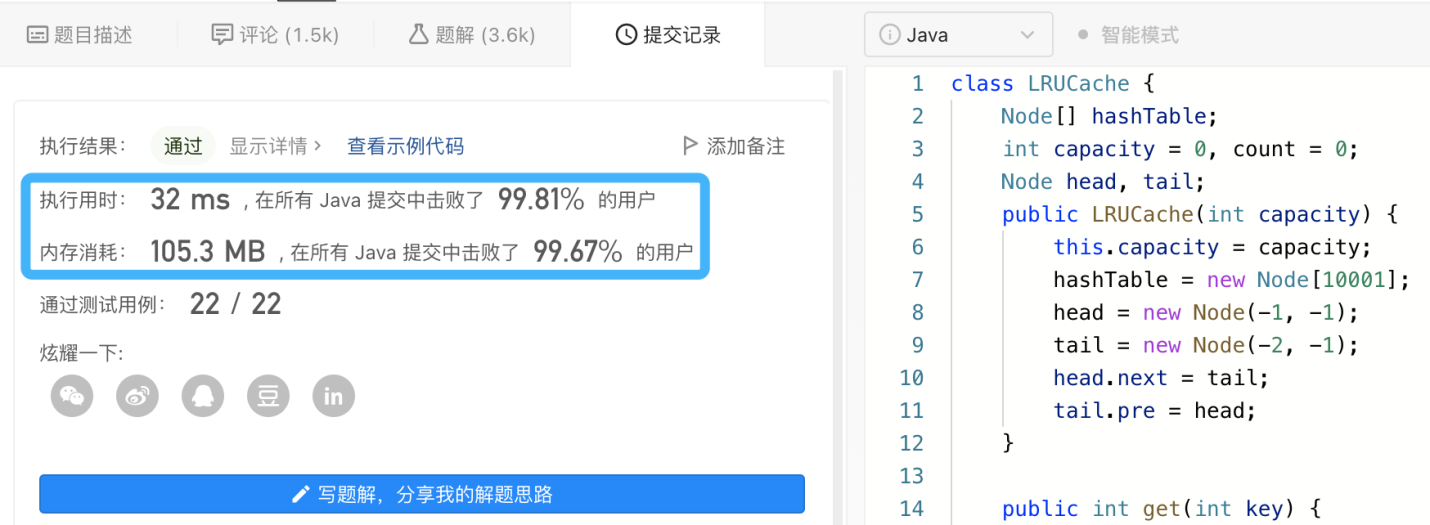
今天的文章内容就这些了:
写作不易,笔者几个小时甚至数天完成的一篇文章,只愿换来您几秒钟的 点赞 & 分享 。
更多技术干货,欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享,每天更新」