2022年天府杯全国大学生数学建模竞赛

B题 第一“君”情

原题再现：

  近日俄罗斯和乌克兰的冲突日益加剧，不难发现现代战争仍然是以人为主的战争，并未进入到全机械化的战争状态。那么在战争中军事物资的补给显得十分重要，中国古代兵法中讲到“兵马未动，粮草先行”就是这一点的体现。现代战争中，士兵往往不会一次性带上大量的食物和弹药，如果陷入了较为持久的战斗状态则需要调动补给站中的后勤部队快速补充物资。
  在某地的补给站附近，同时有 4 支部队需要补充物资，而补给站有 A,B 两种类型的飞机，A 类飞机有 6 架,最大载重 13 吨，飞行速度 260km/h；B 类飞机有 10 架,最大载重 20 吨,飞行速度 50km/h.飞机可以沿直线前往部队投放物资，且每次只能前往一个目的地投放物资，投放结束需要回到补给站再前往下一个部队投放物资。
  每支部队可以接受多于所需要的物资，但接受的物资数量不能超过所需数量的 150%。飞机装卸也需要时间，A 类飞机装卸均为 20min；B 类飞机装载货物需要 30min，卸载货物需要 40 分钟。
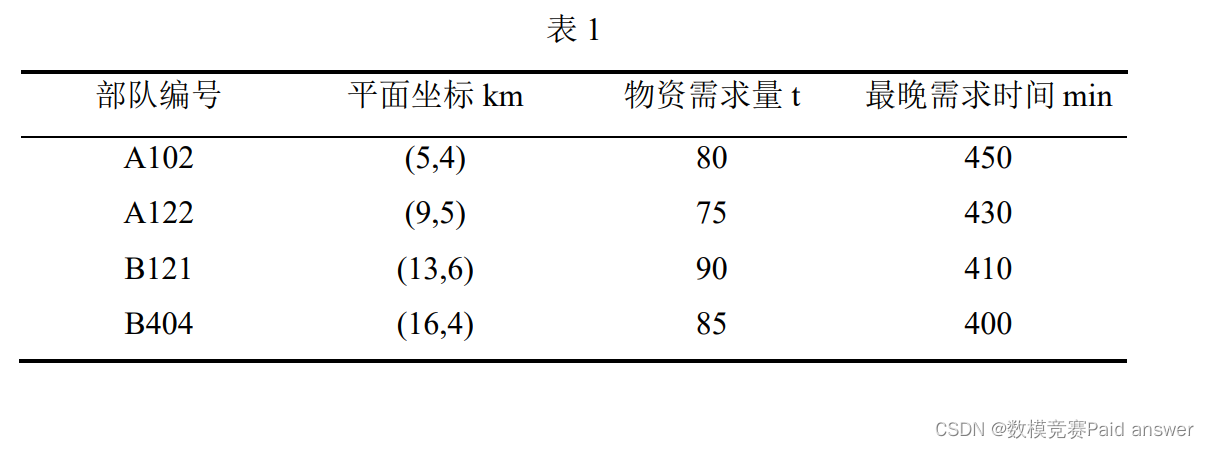
  由于军情紧急，物资全部运送完成的时间不得超过该部队的最晚需求时间。4 支部队的坐标、请求物资的数量最晚的需求时间见表 1。现在该补给站邀请你作为飞机调度的决策者，请解决以下问题：
  （1）假设旧补给站被敌军炸毁，需要紧急建设新补给站。不考虑其他因素，仅仅考虑能最大程度给各个部队提供支援，请建立合适的数学模型确定新补给站的修建地点。
  （2）由于种种原因，新补给站被修建在坐标为(10,30)的位置，请建立数学模型确定飞机的调用方案。
  （3）各个部队接到上级要求需要再收到补给后继续移动前往下一个地点执行任务，因此不能携带超过所需数量 110%的物资，且由于搬运过程中 A 类飞机会有5%-10%的损耗，B类飞机有3%-7%的损耗。请建立数学模型确定转运方案。

整体求解过程概述(摘要)

  军事物资的补给是战争中一项非常重要的工作，一场战争陷入较为持久的战斗时则需要调动补给站中的后勤部队快速补充物资，所以研究战争物资调度问题很有意义。
  针对问题一，首先将题目要求转化为相应的数学问题，以新建补给站到各个部队的总距离最短表示最大程度给各个部队提供支援，由此可以建立无约束优化模型，自变量即新建补给站的位置坐标。本文采用两种方法求解无约束问题，分别为梯度下降法和鲸鱼优化算法。两种算法求解的结果分别为（10.49，5.05）和（9.0055，4.9992），对比发现，鲸鱼优化算法求解的最优位置正是部队 A122，因此从战争因素考虑将补给站设置在（10.49，5.05）最好，到四个部队的总距离为 15.3737km。
  针对问题二，首先，将题目要求的确定飞机调用方案转化为最小化完成所有运输任务的时间，并以此为目标函数，最晚需求时间、飞机超出物资数量要求、飞机总数量为约束条件建立单目标整数规划模型，明确自变量为 6 架飞机 A 和10 架飞机 B 的调度方案。考虑智能优化算法在本问中对产生新解的要求过高，本问采用贪心算法求解模型二。结合两种飞机的属性，将每次调度均选择距离补给站最远的部队和优先考虑 B 类飞机为贪心方式，求解得到的结果是派遣 4 架 B飞机去部队 A102、5 架 A 飞机和 1 架 B 飞机去部队 A121、7 架 A 飞机去部队B121 和 5 架飞机去部队 B404，完成所有任务的运输时间为 102.01 分钟。最后，改动贪心算法的贪心方式对模型进行检验，结果显示，改变后的贪心算法并不能改变最短时间，但是会影响多出物资的数量，证明了模型二是可靠的。
  针对问题三，首先，在问题二模型的基础上，引入最小化多出物资为第二个目标函数，调整约束条件超出物资的数量，并考虑飞机运输过程中的损失因素，引入损失因子概念，将不确定的损失因子规定为范围内的期望值，建立多目标整数规划模型。模型三是多目标优化问题，因此贪心算法在模型三中存在很大的限制，本文采用模拟退火算法求解问题三，将最小化完成运输任务的时间转化为约束条件，并考虑新解的产生固定在问题的解空间内，经过 150 次迭代后算法找到的最优解为：派遣 2 架 A 飞机和 3 架 B 飞机去部队 A102、4 架 B 飞机去部队A122、6 架 A 飞机和 1 架 B 飞机去部队 B121、4 架 A 飞机和 2 架 B 飞机去部队B404。此外，模拟退火求解的物资总数为334.3吨，相比于贪心算法的结果370.375吨提高了 10.79%，最短时间仍然可以达到 102.01 分钟。最后，通过调整损失因子的值对参数损失因子进行灵敏度检验，结果显示，当物资损失的程度在期望值的小范围内波动时，模型求解的结果并不会存在很大差异，但是当损失程度过大时，飞机的调度方案将会发生大变化，此时完成所有运输任务的最短时间将会增加 46.98%。

模型假设：

  一、 假设飞机在运送过程中都是装满出发的，不存在一架飞机未装满就出发的情况；
  二、 假设所有的飞机可以同时起飞、同时出发，并且支持并行；
  三、 问题三的补给站位置就是第二问的补给站位置；
  四、 飞机在飞行过程中不会存在耽误时间，默认用给定速度恒定飞行；

问题分析：

  本题要求我们作为飞机调度的决策者，解决三个不同情况下的优化问题。解决这类纯优化类问题，解题思路主要分为两步：第一步明确题目的目标函数，找到题目要求的约束条件；第二步采用优化方法求解模型；对于问题一无约束优化问题，可以借助梯度的方法求解，也可以采用智能优化算法进行求解。对于问题二有约束的整数规划问题，最简单的求解办法就是指定贪心规则，采用贪婪算法求解。对于问题三，需要考虑约束条件的变化以及双目标的选择，本文采用模拟退火算法进行求解。
   问题一的分析
  问题一中假设旧的补给站被敌军炸毁，需要紧急建设新的补给站。不考虑其它因素，仅仅考虑能最大程度给各个部队提供支援，该题的思路分为两个步骤：
  1. 确定题目要求的考虑最大程度给各个部队提供支援的意义，将建站问题转化为数学问题。对附件表格中的数据进行分析，我们发现可以将最大程度给各个部队提供支援理解为新建站到四个部队的总距离最小，于是我们就可以建立无约束优化模型；
  2. 求解无约束的方法各种各样，最主流的方法就是基于梯度的方法，例如梯度下降法、牛顿法和拟牛顿法等等，不基于梯度的方法例如演化算法和群智能算法等等，常见的有模拟退火、遗传算法和粒子群算法等等，本文选择了一种求解能力相较于常规算法更强的群智能优化算法——鲸鱼算法。并对两种算法求解的结果进行了对比分析，给出了在不同现实情况下的建站方案。
   问题二的分析
  在问题二中，由于种种原因，新补给站被修建在坐标为（10，30）的位置，让我们建立数学模型确定飞机的调用方案。在知道新建补给站的坐标位置后，我们就可以使用给定的坐标位置来调度飞机运送物资了，至于如何调度飞机就是第二问需要确定的。同第一问思路类似，我们必须先找到合适的目标函数和约束条件，从而将飞机调度问题转化为规划问题。本文需要考虑多种因素，比如物资全部运送完成的时间不得超过该部队的最晚需求时间、所有飞机的存在最大载重等等。很明显，这是一个整数规划模型，自变量是 16 架飞机的调度情况。目标函数题目并没有明确给出，但是在考虑到实际情况下将目标函数确定为最小化完成运输时间。解决整数规划的方法有很多，例如模拟退火，贪婪算法等等均可，如何选择最优的解决方法需要考虑题目所给的约束条件，本文采用贪婪算法来求解规划模型，相较于模拟退火算法，贪婪算法更加简单，并且贪婪算法不需要像模拟退火一样每次生成在解空间的解，贪婪算法是逐步迭代的，每一步都取最优的，最后总结果即是最优的。最后，我们对贪婪算法求解的结果进行了检验分析，给出了更加精确的改进方案。
  问题三的分析
  问题三是在问题二的基础上加上新的约束条件，即题目明确规定了各个部队需要在收到补给后继续移动前往下一个地点执行任务，因此每个部队所存储的物资量不能超过所需数量的 110%。且在第三问新增加了搬运过程的损耗，且 A 类飞机的损耗和 B 类飞机的损耗不同，这就对模型求解的结果造成了一定的随机性，对于这类带有随机性的问题，我们一般解决的办法有两种。第一种就是将随机性因素转化成固定的因素，从而减小复杂度，但是这样做的结果就是模型的鲁棒性不强。另一种方法就是保持随机性，且每次的决策都需要考虑随机因素，显然这样做将会加大题目的难度。除此之外，在第三问中我们考虑到最优调度不仅仅是时间上最优，调度的结果也需要最优，于是我们引入最小化多出物资为第二个目标函数，建立了多目标整数优化模型。为了简化求解的难度，我们先固定了损耗因子的值，并将最小化运输时间转化为约束条件，从而使双目标模型变为单目标模型，采用模拟退火算法求解模型，最后对模型的损耗因子参数进行了灵敏度分析。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

部分程序代码：(代码和文档not free)

1. clc   
2. clear   
3.    
4. % 绘图函数  
5. % draw  
6.    
7. % 求最优位置  
8.    
9. % 鲸鱼算法  
10.% 参数初始化  
11.a = 2; % 初始游动因子的值，后续会不断缩减  
12.MAX_iter = 200; % 迭代次数  
13.iter = 1; % 初始化迭代次数  
14.b = 3; % 螺旋系数  
15.number = 100; % 定义鲸鱼的数量  
16.fitt = zeros(number,1); % 初始化适应度  
17.x = zeros(number,2); % 初始化种群  
18.l_min = ‐100; %自变量下界  
19.l_max = 100; % 自变量上界  
20.for i = 1:number % 初始化种群和适应度  
21.    x(i,1) = l_min + rand(1) * (l_max ‐ l_min);  
22.    x(i,2) = l_min + rand(1) * (l_max ‐ l_min);  
23.    fitt(i) = fit(x(i,:));  
24.end   
25.fit_best = min(fitt); % 记录最优适应度  
26.ind = find(fitt == min(fitt),1);  
27.X_best = x(ind,:); % 记录最优位置  
28.X_BEST = []; % 记录全局  
29.FITT = []; % 记录全局  
30.%% 迭代开始  
31.while iter <= MAX_iter  
32.    for i = 1:number  
33.        if rand() < 0.5 % 采用游动捕食  
34.            a = 2 * (1 ‐ iter / MAX_iter); % 更新游动因子  
35.            r = rand(1,2); % 随机数  
36.            C = 2 * r; % 计算摆动因子  
37.            A =  2 * r * a ‐ a; % 计算收敛因子  
38.            if sqrt(A(1)^2 + A(2)^2) < 1 % 采取包围捕食  
39.                D = abs(C .* X_best ‐ x(i,:)); % 计算最优距离  
40.                x(i,:) = X_best ‐ A .* D; % 这里是位置更新  
41.                if x(i,1) < l_min || x(i,1) > l_max % 判断是否超
出边界
42.                    x(i,1) = l_min + rand(1) * (l_max ‐ l_min);
43.                end   
44.                if x(i,2) < l_min || x(i,2) > l_max  
45.                    x(i,2) = l_min + rand(1) * (l_max ‐ l_min);
46.                end   
47.            else % 采取随机游动  
48.                rand_ind = unidrnd(20); % 随机抽取鲸鱼  
49.                D = abs(C .* x(rand_ind,:) ‐ x(i,:));  
50.                x(i,:) = x(rand_ind,:) ‐ A .* D;  
51.                if x(i,1) < l_min || x(i,1) > l_max % 判断是否超
出边界  
52.                    x(i,1) = l_min + rand(1) * (l_max ‐ l_min);
53.                end   
54.                if x(i,2) < l_min || x(i,2) > l_max  
55.                    x(i,2) = l_min + rand(1) * (l_max ‐ l_min);
56.                end   
57.            end   
58.        else % 采用气泡捕食  
59.            D_1 = abs(X_best ‐ x(i,:));  
60.            l = unifrnd(‐1,1); % 随机数  
61.            x(i,:) = D_1 * exp(b * l) * cos(2 * pi * l) + X_best
;  
62.            if x(i,1) < l_min || x(i,1) > l_max % 判断是否超出边
界  
63.                x(i,1) = l_min + rand(1) * (l_max ‐ l_min);  
64.            end   
65.            if x(i,2) < l_min || x(i,2) > l_max  
66.                x(i,2) = l_min + rand(1) * (l_max ‐ l_min);  
67.            end   
68.        end   
69.        fitt(i) = fit(x(i,:)); % 每更新一次位置，求解一次适应度  
70.    end   
71.    disp(['当前迭代次数为：',num2str(iter)])   
72.    % 迭代完一次更新数据  
73.    fit_best = min(fitt); % 更新当前代数中种群的最优解  
74.    ind = find(fitt == min(fitt),1);  
75.    X_best = x(ind,:); % 更新最优位置  
76.    X_BEST = [X_BEST;X_best]; 
77.    FITT = [FITT;fit_best];  
78.    iter = iter + 1;  
79.end   
80.Fit_Best = min(FITT);  
81.ind_best = find(FITT == min(FITT),1);  
82.X_BE = X_BEST(ind_best,:);  
83.disp(['找到的最优解为：',num2str(Fit_Best)])   
84.disp(['最优解对应的 X：',num2str(X_BE)])   
85.figure(2)   
86.plot(1:MAX_iter,FITT)  
87.title('种群迭代图')   
88.xlabel('迭代次数')   
89.ylabel('适应度值') 

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可