生活中大家从小到大处处可见排队,但是排队有哪些快速的方法你了解吗?

八大排序
- 排序的基本概念
- 插入排序
- 直接插入排序
- 基本思想
- 代码
- 直接插入排序总结
- 希尔排序
- 基本思想
- 代码
- 希尔排序总结
- 选择排序
- 直接选择排序
- 基本思想:
- 代码
- 直接选择排序总结
- 堆排序
- 堆的基本概念
- 向下调整算法
- 堆排序的基本思想(大堆)
- 代码
- 堆排序总结
- 结语
排序的基本概念
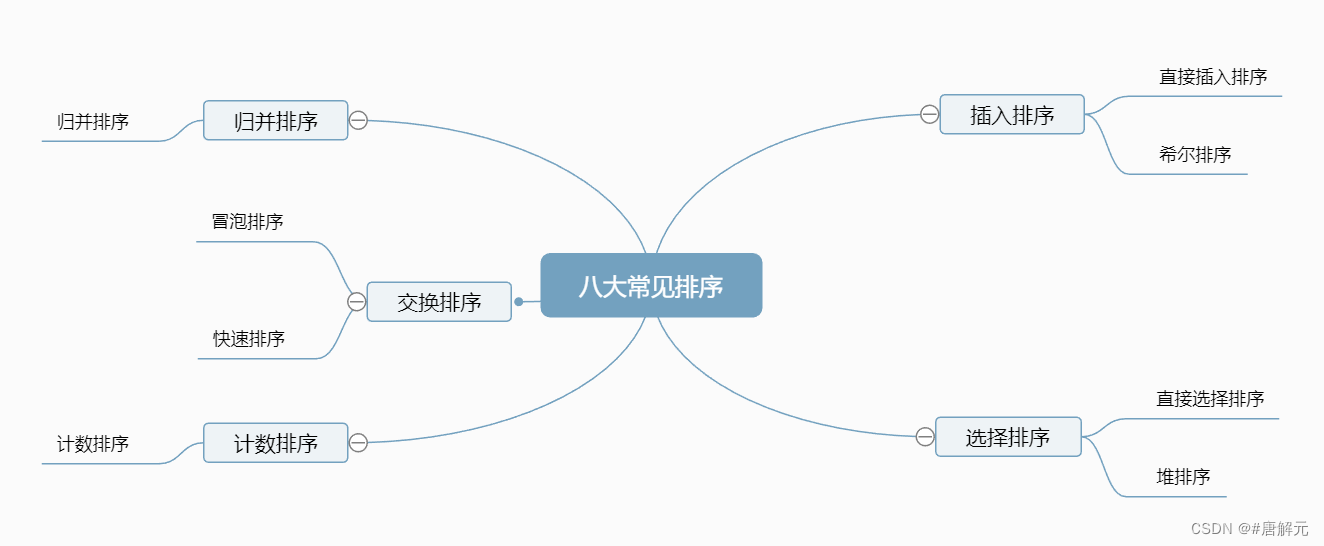
- 排序 (Sorting) : 是计算机程序设计中的一种重要操作,它的功能是将一个数据元素(或记录)的任意序列,重新排列成一个按关键字有序的序列;
- 稳定性: 假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
- 内部排序: 指的是待排序记录存放在计算机随机存储器中进行的排序过程;
- 外部排序: 指的是待排序记录的数量很大,以致内存一次不能容纳全部记录,在排序过程中尚需对外存进行访问的排序过程。
插入排序
直接插入排序
基本思想
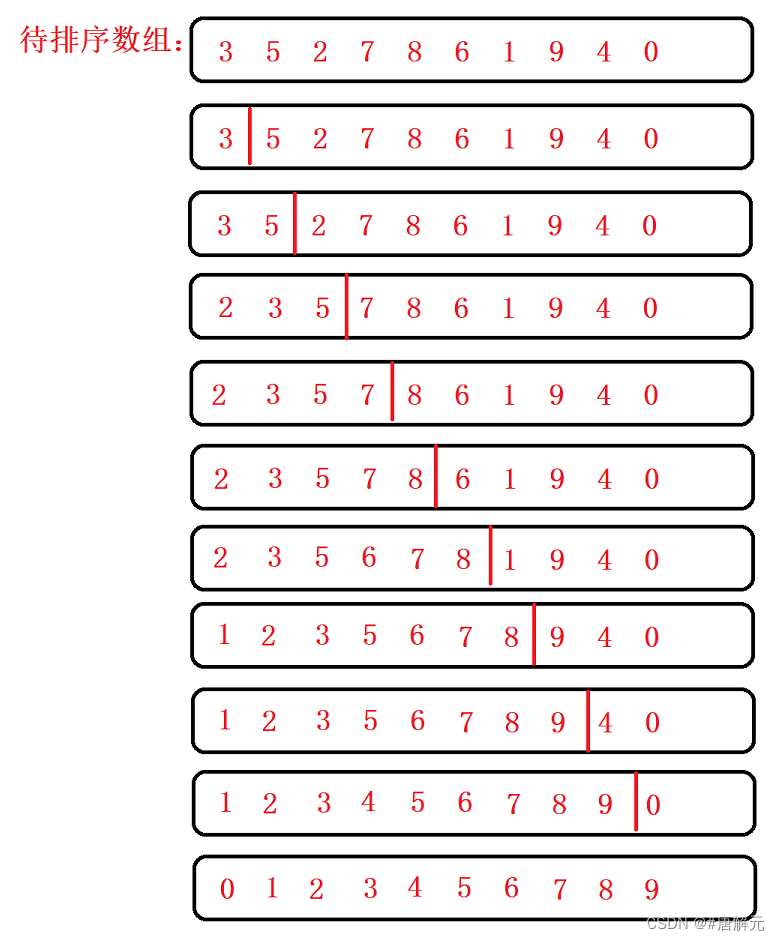
- 直接插入是一种最简单的排序方法,它的基本操作是将一个记录插入到已排好序的有序序列中,从而得到一个新的,记录数增1的有序表;
- 先将序列中的第1个记录看成是一个有序的子序列,然后从第2个记录起逐个进行插入,直至整个序列变成有序序列为止,整个排序过程进行n-1趟插入;
- 直接插入排序就像是大家斗地主一样😁😁😁,假定我们手中已经有了[0,end]张有序的牌,这时我们摸了一张牌,将新摸得这张牌插入到我们手中[0,end]里,并使[0,end+1]有序。
代码
void InsertSort(int* a, int n)
{
//[0,end]有序,把 end+1位置的值插入[0,end],让[0,end+1]有序
for (int i = 0; i < n - 1; ++i)//这里的for循环,就相当于摸牌,n-1就相当于斗地主中,非地主一共摸几张
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
void TestInsertSort()
{
int a[] = { 3,5,2,7,8,6,1,9,4,0 };
InsertSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
直接插入排序总结
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 稳定性:稳定
希尔排序
希尔排序是直接插入排序的优化,又被称为“缩小增量排序”,虽然它也是一种属插入排序类的方法,但是时间效率相比直接插入排序有较大改进。😎😎😎
基本思想
大致分为两步:1.预排序让数组接近有序,2.直接插入排序(上面直插总结,元素越接近有序,直插效率越高)。
先选一个整数(gap),把数组中间隔为gap的分为一组,并将每组排好序,再让gap/2,并重复分组和排序,当gap=1时,数组中就排好序了。 其中每组排序用的是直接插入排序
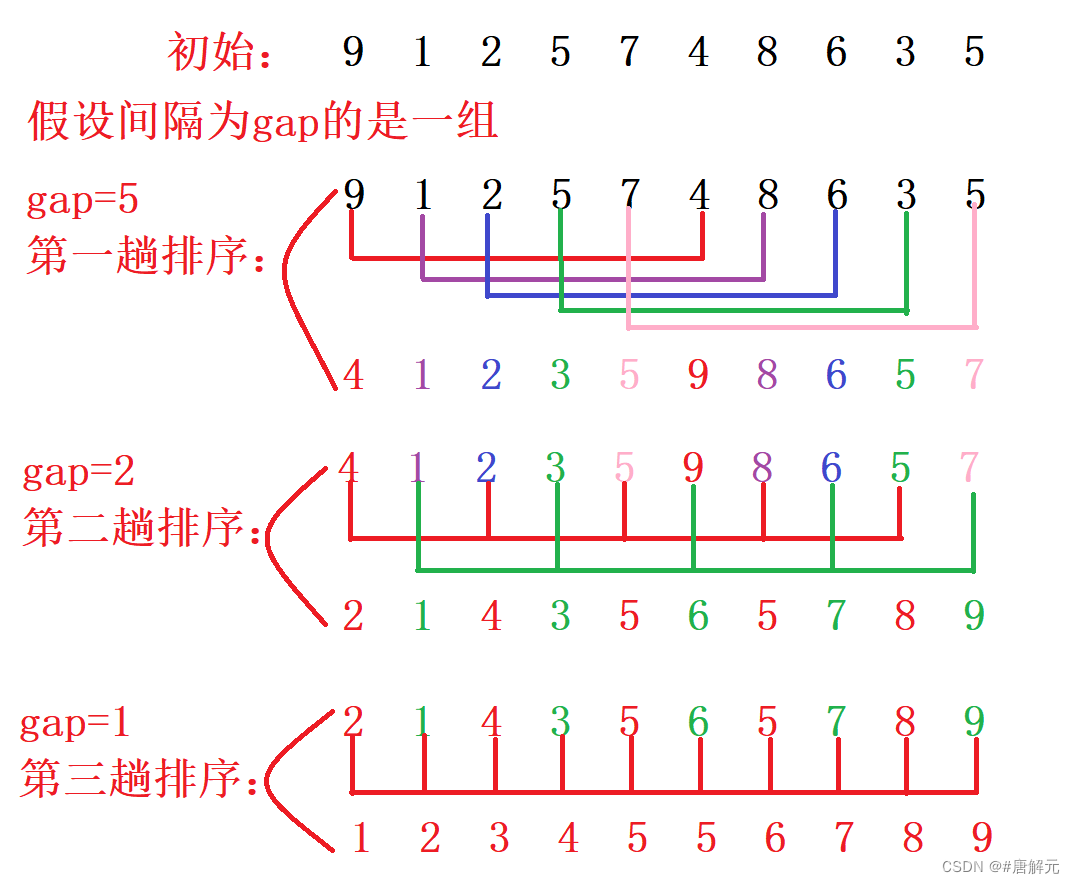
- 多组间隔为gap的预排序,gap由大变小;
- gap越大,元素中最大和最小越快到它相应地位置,但是预排越不接近有序;
- gap越小,越接近有序;
- gap等于1时,那就成直接插入排序了。
代码
void ShellSort(int* a, int n)
{
int gap=n;
while (gap > 1)
{
//gap=gap/3+1;
gap = gap / 2;//除三或者除二都是可以的,除二的话能保证最后gap一定为1
// gap>1时都是预排序--目的使其接近有序
// gap==1时就是直接排序
//gap很大时,下面预排序的时间复杂度是O(N)
// gap很小时,数组已经很接近有序了,这是差不多是O(N)
//把间隔为gap的多组数据同时排
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
void TestShellSort()
{
int a[] = { 9,8,7,6,5,4,3,2,1,0 };
ShellSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
希尔排序总结
- 希尔排序是对直接插入排序的优化;
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,就成直接插入排序;
- 稳定性:不稳定;
- 时间复杂度:挺难算的,前辈求出的是 O(N^1.3——N ^2)。
选择排序
直接选择排序
基本思想:
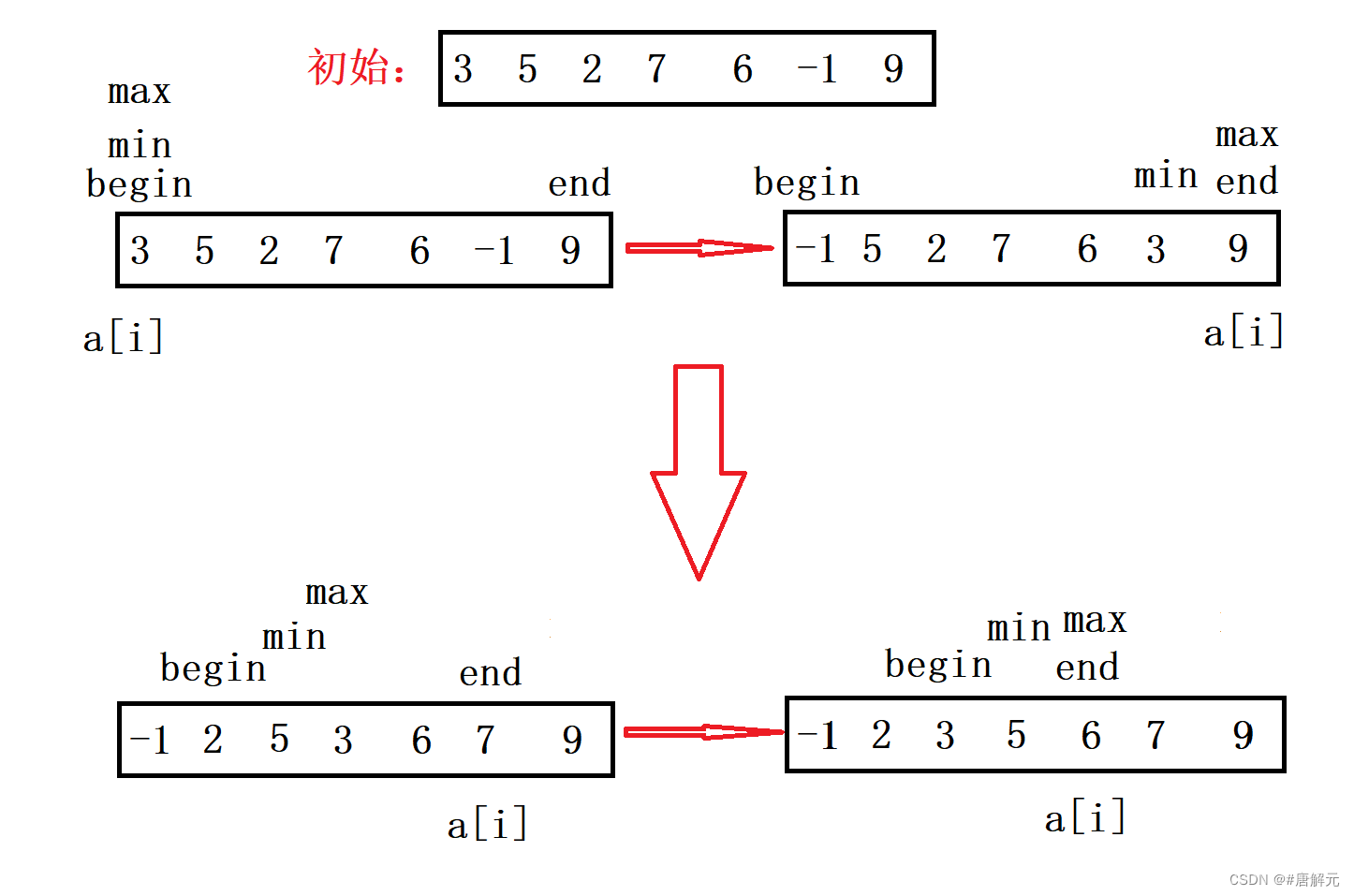
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,最大的放到序列的最后面,直到全
部待排序的数据元素排完 。😧😧😧
实现
- 在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素;
- 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)
元素交换; - 在剩余的array[i]–array[n-2](array[i+1]–array[n-1])集合中,重复上述步骤,直到集合剩
余1个元素。
代码
void Swap(int*p1,int*p2)//交换
{
int* tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int min = begin, max = begin;
for (int i = begin; i <= end; ++i)
{
//分别选出数组中最大的数和最小的数,分别赋给min和max;
if (a[i] < a[min])
{
min = i;
}
if (a[i] > max)
{
max = i;
}
}
Swap(&a[begin], &a[min]);
// 如果begin跟max重叠,需要修正一下max的位置
if (begin == max)
{
max = min;
}
Swap(&a[max], &a[end]);
++begin;
--end;
}
}
void TestSelectSort()
{
int a[] = { 3, 5, 2, 7, 8, 6, -1, 9, 9, 4, 0 };
SelectSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
直接选择排序总结
- 直接选择排序很简单,只看代码就能轻松理解,但是实用性很低,大家了解即可;
- 时间复杂度:O(N^2);
- 稳定性:不稳定。
堆排序
堆的基本概念
之前在二叉树中写过链式结构,今天的堆排序顺带着给大家写一下二叉树的顺序结构。
堆的逻辑结构与物理结构
- 堆的逻辑结构是一颗完全二叉树(想象出来的),堆的物理结构是一个数组。
堆的两大特性
- 结构性:用数组表示的完全二叉树;
- 有序性:任一结点的关键字是其子树所有结点的最大值(或最小值)
1.“最大堆”,也称为“大顶堆”: 最大值,要求:树中所有父亲都大于等于孩子;
2.“最小堆”,也称为“小顶堆”: 最小值,要求:树中所有父亲都小于等于孩子;
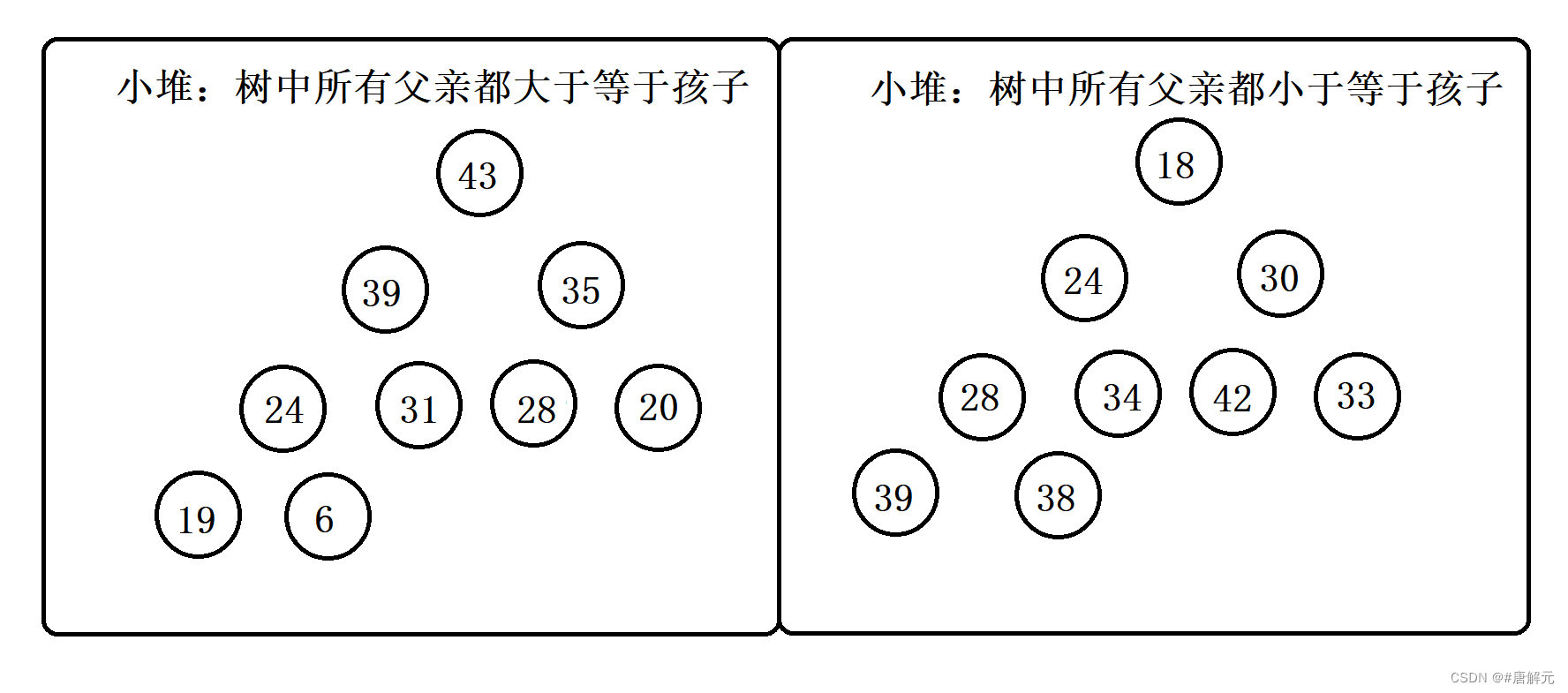
从上图我们发现,小堆它的根一定是最小的,而大堆的根一定是最大的。
父子间下标的关系
leftchild是左孩子结点,rightchild是右孩子结点,parent是父亲结点,child是孩子结点 - leftchild=parent*2+1;
- rightchild=parent*2+1+1=leftchild+1;
- parent=(child-1)/ 2。
向下调整算法
建小堆:选出左右孩子中小的哪一个,跟父亲交换,小的往上浮,大的往下沉,如果要建大堆则相反
向下调整算法前提
- 若想将其调整为小堆,那么根结点的左右子树必须都为小堆。
- 若想将其调整为大堆,那么根结点的左右子树必须都为大堆。
向下调整算法基本思想(以小堆为例子)
- 从根结点处开始,选出左右孩子中值较小的孩子;
- 让小的孩子与其父亲进行比较;
- 若小的孩子比父亲还小,则该孩子与其父亲的位置进行交换。并将原来小的孩子的位置当成父亲继续向下进行调整,直到调整到叶子结点为止;
- 若小的孩子比父亲大,则不需处理了,调整完成,整个树已经是小堆了。
如何选择建大堆还是小堆?
- 升序建大堆,因为大堆的根节点是整颗树的最大值;
- 降序建小堆,因为小堆的根节点是整颗树的最小值。
堆排序的基本思想(大堆)
因为我们这里用到的是升序,所以就用大堆的方式
先将一个数组构建一个大顶堆,此时,最大值就是根结点,将其与末尾元素进行交换,这时末尾就是最大值,然后再将剩余n-1个元素再次构建一个大顶堆,以此循环,就可以得到一个有序序列。😋😋😋
代码
//交换两个变量--传址调用
void Swap(int*p1,int*p2)
{
int* tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//向下调整算法--大堆
void AdjustDwon(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])
{
child += 1;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDwon(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDwon(a, end, 0);
--end;
}
}
void TestHeapSort()
{
int a[] = { 3, 5, 2, 7, 8, 6, 1, 9, 4, 0 };
HeapSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
堆排序总结
- 堆排序用堆来选数,效率是很高的
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
结语
😊😊😊到了这里大家对于插入排序和选择排序这两类已经基本掌握了,下篇会得大家带来冒泡排序,三种快速排序,计数排序和归并排序。😚😚😚