力扣
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
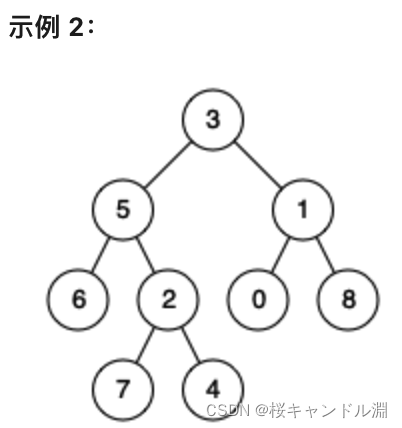
示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:输入:root = [1,2], p = 1, q = 2
输出:1
提示:
树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
一个节点也可以是自己的祖先。
沿着根节点到当前结点的路径上的所有的结点都可以是自己的祖先
如果这里是三叉链,结点带parent,转换成链表相交的做法就可以了,
但是很可惜,这里并不是三叉链
规则:一个是左子树中的结点,一个是右子树中的结点,那么他就是最近公共祖先
1.如果这两个结点在我的左子树和右子树当中,那么我就是这两个结点的最近公共祖先
2.如果这两个结点都在我的左边,那么我就去查找我的左子树是不是最近公共祖先
3.如果这两个结点都在我的右边,那么我就去查找我的右子树是不是最近公共祖先
4.如果我就是其中的一个要查找的结点,另外一个结点是我的孩子,那么我就是最近公共祖先
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool Find(TreeNode* sub,TreeNode* x)
{
if(sub==nullptr)
{
return false;
}
if(sub==x)
{
return true;
}
//去当前结点的左子树去找x,或者去右子树去找x,只要有一个地方找到就行
return Find(sub->left,x)||Find(sub->right,x);
}
// 如果这两个结点在我的左子树和右子树当中,那么我就是这两个结点的最近公共祖先
// 如果这两个结点都在我的左边,那么我就去查找我的左子树是不是最近公共祖先
// 如果这两个结点都在我的右边,那么我就去查找我的右子树是不是最近公共祖先
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==nullptr)
return nullptr;
// 如果我就是其中的一个要查找的结点,另外一个结点是我的孩子,那么我就是最近公共祖先
if(root==p||root==q)
return root;
bool p_In_Left,p_In_Right,q_In_Left,q_InRight;
//到我当前结点的左子树中去寻找p,如果找到了,就不要再往右子树当中找了
p_In_Left=Find(root->left,p);
//如果p在左边,那么就一定不在右边
//因为我们的p一定在这棵树里面
p_In_Right=!p_In_Left;
//如果q在左边,那么就一定不在右边
//因为我们的q一定在这棵树里面
q_In_Left=Find(root->left,q);
q_InRight=!q_In_Left;
//1、一个在左,一个在右,那么root就是最近公共祖先
//2、如果都在左,那么递归去左子树找
//3、如果都在右,那么递归去右子树找
if((p_In_Left&&q_InRight)||(q_In_Left&&p_In_Right))
{
return root;
}
//2、如果都在左,那么递归去左子树找
else if(p_In_Left&&q_In_Left)
{
return lowestCommonAncestor(root->left, p,q);
}
//3、如果都在右,那么递归去右子树找
else if(p_In_Right&&q_InRight)
{
return lowestCommonAncestor(root->right, p,q);
}
else
{
//理论而言,不会走这里。
return nullptr;
}
}
}; 
如果我们的要查找的两个结点越在我们的树的下面的结点,我们的上面这种算法的时间和空间开销就越大。
这里的find的时间复杂度就是O(N)
最多要找二叉树高度次(H)
也就是时间复杂度为O(N*H)
如果这里是一棵搜索二叉树,也就是左子树比根节点小,右子树比根节点都打,那我们就不需要这里的find函数了,也就可以提升我们的效率了。
如何从O(N*H)优化到O(N),
如果我们这道题能够找到根节点到目标节点的路径,那么我们就能够转换为链表相交的方法去做了。现在我们就可以尝试寻找这两条路径
(这里我们按照前序遍历)
如果我们这里寻找6,当前我们的根节点,
3不是6,入栈3
5不是6,5入栈
6是6,找到了,再层层返回出栈
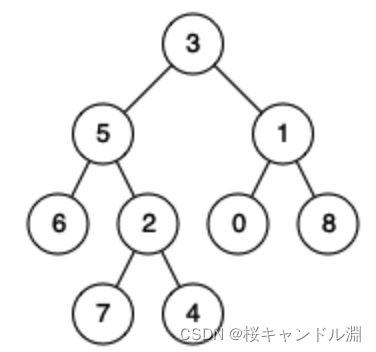
如果我们现在要找4,
3不是4,入栈4
5不是4,入栈5
6不是4,入栈6
6的左右都是nullptr,都返回的是false
此时我们可以确定6这棵子树下面没有我们的目标结点了,将6出栈
接着2不是4,入栈2
7不是4,入栈2
7的左右结点都是nullptr,返回都是false
此时我们可以确定7这棵子树下面没有我们的目标节点了,将7出栈
4是我们的要找的结点,返回true,停止查找。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool FindPath(TreeNode* root,TreeNode* x,stack<TreeNode*>& path)
{
//这里返回的false和true都是提供给上一层的。
if(root==nullptr)
return false;
path.push(root);
if(root==x)
return true;
//左树找到了,右树就不要找了
if(FindPath(root->left,x,path))
return true;
//左树没找到,就再去右树找
if(FindPath(root->right,x,path))
return true;
//左树和右树都没有找到
path.pop();
//这里的false代表当前子树里面没有我们想要查找的结点
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//创建两个栈用于存储从根节点到目标节点的路径
stack<TreeNode*> pPath,qPath;
FindPath(root,p,pPath);
FindPath(root,q,qPath);
//类似链表相交
//让长的先走
while(pPath.size()!=qPath.size())
{
//我们的栈刚好是反着存的,也就是树的底部的结点存在栈的顶部,root结点在栈的底部
if(pPath.size()>qPath.size())
pPath.pop();
else
qPath.pop();
}
while(pPath.top()!=qPath.top())
{
pPath.pop();
qPath.pop();
}
//这两个路径是一定会有交点的
//这里返回pPath或者qPath的top都是可以的。
return pPath.top();
}
}; 
这一种思路就是将我们的时间复杂度降低到了O(N),也就是最多遍历一遍二叉树的所有结点。并且我们这一种方法相较于我们的上一种方法,由于我们这里开辟了两个栈,所以空间复杂度比较大。