2022年天府杯全国大学生数学建模竞赛

A题 仪器故障智能诊断技术

原题再现：

  问题背景：
  仪器设备故障诊断技术是一种了解和掌握机器在运行过程的状态，确定其整体或局部正常或异常，早期发现故障及其原因，并能预报故障发展趋势的技术。仪器故障按照来源可分为外部型和内部型，其中外部型故障的产生多为静电放射、电磁辐射、雷暴天气、空气湿度过大等导致的电路损坏或传感器失灵，内部型故障多为齿轮破裂、电机短路等。油液监测、振动监测、噪声监测、性能趋势分析和无损探伤等为其主要的诊断技术方式。
  随着计算机技术和人工智能科学的发展，基于机器学习或深度学习的故障智能诊断方法成为从业者的新型决策工具，其中故障类型识别是主要内容，该项技术特点在于：降低原始数据的环境噪声或异常数据影响，提取可靠的波形特征判据，选择或改进现有的机器学习方法，设计一系列必要的仿真实验，讨论与分析。
  请解决：
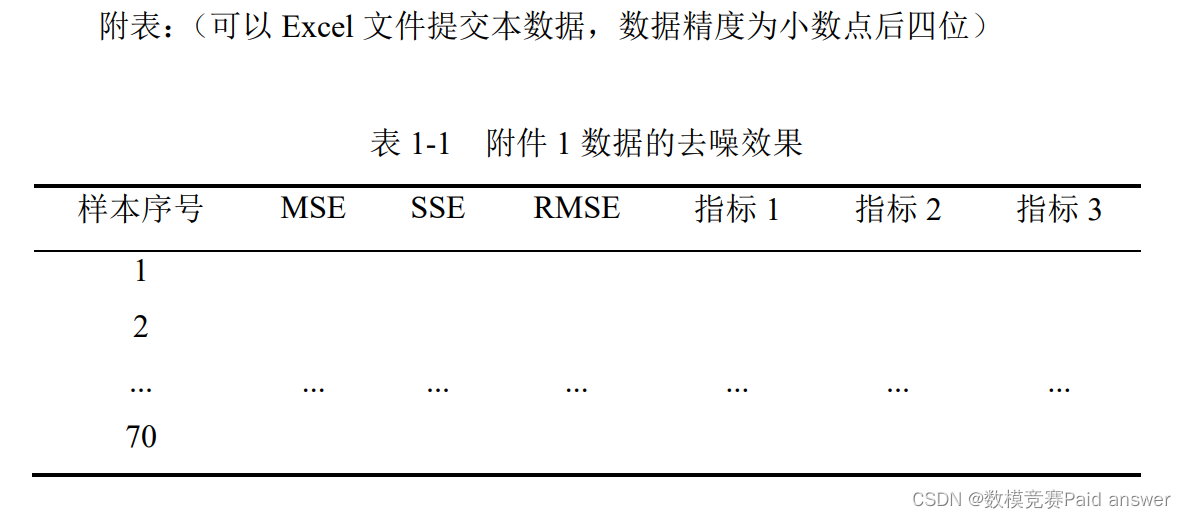
  （1）针对附件一和附件二中的数据，各自由选择 1 条原始数据进行信号去噪处理，并将处理效果汇总在附表 1-1 和附表 1-2 中，表中指标已存在 3 项，另需参赛者添加至少 3 项评价指标，以完善故障数据去噪效果评价；
  （2）信号特征提取是进行故障智能检测的重要前提。请针对附件一和附件二中的全部数据进行信号的特征提取，特征判据数量不得少于 10 项，并将提取的特征值汇总在附表 2-1 和附表 2-2 中；
  （3）基于无监督型或半监督型方法，进行附表 1 类数据和附表 2 类数据的二分类实验，并将实验结果登记在附表 3 中，预测结果评价指标已存在 3 项，另需参赛者添加至少 3 项评价指标，使用的预测方法应保证预测准确率均值在 90%以上，准确率标准差在 10 以内；
  （4）基于有监督型学习方法，进行附表 1 类数据和附表 2 类数据的二分类实验，并将实验结果登记在附表 4 中，预测结果评价指标已存在 3 项，另需参赛者另添加至少 3 项评价指标，使用的预测方法应保证预测准确率均值在 95%以上，准确率标准差在 5 以内；
  （5） 本问属于选择题，参赛者可在下列 3 个小问中任选一问解答：
  5.a 请对比分析信号去噪前后的信号特征在信号分类试验中的区别与影响；
  5.b 讨论特征的数量以及质量对特征识别的影响，以及给出解决办法；
  5.c 引入图像识别技术解决第三问或第四问。

  附件数据说明：文件名依次为 1～100，1～70 为 A 型故障数据，71～100 为B 型故障数据；每条数据长度统一为 4096，已做归一化处理，值域范围为[-1,+1]。

整体求解过程概述(摘要)

  本文主要通过分析仪器设备产生的波形信号数据，提取重要信号特征，进而达到对设备仪器的故障智能检测。根据信号数据的特点，我们对问题 1 绘制箱线图对异常值进行降噪处理；对问题 2 用主成分分析法提取主成分特征，再用随机森林算法提取重要特征；对问题 3 用 K-均值聚类算法、高斯混合分布进行设备故障的分类；对问题 4 用随机森林及其优化、高斯朴素贝叶斯的方法进行设备故障的分类；对问题 5 用控制变量法解决“提取特征数量以及质量对特征识别的影响”的问题。
  对于问题 1，我们新添 3 个指标分别为 R-Square、MAE、MAPE。首先建立“箱线图异常点调整模型”。然后用 Python编译环境，计算每一列数值的箱线图的上边缘值和下边缘值。将每一列所有异常点调整至上、下边缘值之间。最后，用 Python绘制每一列数据调整前和调整后的箱线图进行比较，分析 6 项指标以验证模型降噪的合理性，并将处理后的结果汇总在附表 1-1 和 1-2 中。
  对于问题 2，我们首先读取降噪后的数据，在已搭配环境下运用主成分分析法建立“主成分特征提取模型”。在对该模型的基础之上运用随机森林算法建立“重要性特征提取模型”。在对两个模型合理的理论证明和推导后，从“主成分特征提取模型”中得到72 个主成分特征，再从“重要性特征提取模型”中提取更为重要的 16 个特征，最终得到维度为 100×16 的样本特征数据，并将其结果汇总在附表 2-1 和 2-2 中。
  对于问题 3，我们新添 3 个指标分别为精确率、F1-score、错误率。读取问题 2 得到的样本特征数据，在已搭建环境下构建“K-均值聚类算法模型”，预测准确率均值为58%，但未能达到题意要求。再根据高斯分步函数建立“混合高斯模型”。最终得到样本预测准确率均值为 91%，准确率标准差为 0.29。
  对于问题 4，我们用问题 2 中提取到的样本特征数据，在表中给两类故障分别加上标签。首先，在已搭配环境下用多种分类器给数据进行分类，得到最高分类准确率分别是随机森林分类器和高斯朴素贝叶斯分类器，且准确率都为 90%。在此基础之上我们运用控制变量法以及模型得分准则对参数进行调整，运用特殊的训练集和测试集划分进行改进，进而建立 “随机森林模型”和 “高斯朴素贝叶斯模型”。最终得到“随机森林模型”中分类器的准确率为 93.33%，预测准确率均值为 90%；“高斯朴素贝叶斯模型” 中分类器的准确率为 95%，预测准确率均值为 97%。
  对于问题 5，我们利用主成分分析法提取贡献率累计达到 95%的 72 个特征，利用 100个样本数据的 72 个特征在随进森林和高斯朴素贝叶斯分类器中进行分类，得出分类准确率分别为 83.33%和 86.67%。再利用随进森林分类器对 100 个样本进行单一特征分类，从而选取最佳特征组合，得到最终分类结果为 90%。

模型假设：

  1. 假设题目所给的数据真实可靠；
  2．假设不同仪器设备之间运行时不会相互影响；
  3．假设所有仪器设备信号数据都在相同运行时间段截取；
  4．假设所有仪器设备都在同一环境下运行；
  5．假设所有仪器设备使用年限一样。

问题分析：

  (一) 问题 1 的分析
  问题 1 要求我们对附件数据进行降噪处理，新添 3 项指标。降噪目的是找出噪声并减少或排除噪声对后续工作的影响。分析 6 项指标对降噪效果进行评价，以检验模型降噪的合理性。
  问题 1 属于数据预处理问题。读取原始数据，首先建立“箱线图异常点调整模型”。计算每一列数值的箱线图的上边缘值和下边缘值。将每一列数值大于该列上边缘值的异常点调整为上边缘值，并将每一列数值小于该列下边缘值的异常点调整为下边缘值。最后，绘制数据调整前和调整后的箱线图进行比较，并通过 6 项评估该模型的合理性。
  (二) 问题 2 的分析
  问题 2 属于提取主要特征的数学问题，要求我们在降低数据维度的同时要提取最重要的特征。
  问题 2 一般的数据降维分析方法有奇异值分解、主成分分析、因子分析以及独立成分分析等。由于题中所给数据为 4096 列信号数据，而主成分分析法适合对信号数据进行处理。因此，我们先建立“主成分特征提取模型”，然后在该模型基础上再建立“重要性特征提取模型”。最后，将这两个模型提取的样本特征数据分别在多种分类器中进行二分类，通过分类准确率验证特征模型的合理性。
  (三) 问题 3 的分析
  问题 3 要求我们运用无监督学习方法对两类数据进行分类并新添 3 项指标。
  问题 3 属于无标签分类问题，读取问题 2 的样本特征数据。我们先构建“K-均值聚类算法模型”，然后通过高斯分步概率密度函数建立“混合高斯模型”。将每一个未测试的样本作为测试集，将其余 70%样本作为模型训练集，30 作为测试集。最后记录 6 项指标。最后，通过比较两个模型分类的准确率，得到最终符合要求的模型。
  (四) 问题 4 的分析
  问题 4 要求我们运用有监督学习方法对两类数据进行分类并新添 3 项指标。问题 4 属于分类问题，读取问题 2 的样本特征数据，在表中给两类故障分别加上标签。首先，通过多种分类器以及参数调整优化建立“随机森林分类器模型”，和 “高斯朴素贝叶斯模型”。最后，通过比较两个模型分类的准确率，得到最终符合要求的模型。
  (五) 问题 5 的分析
  问题 5 要求我们讨论并解决特征的数量以及质量对特征识别的影响。对于问题 5，我们利用主成分分析法提取贡献率累计较高的多个特征，利用 100 个样本数据的这些特征在随进森林和高斯朴素贝叶斯分类器中进行分类，得出分类准确率。再利用随进森林分类器对 100 个样本进行单一特征分类，从而选取最佳特征组合，可得得到最终分类结果。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

部分程序代码：(代码和文档not free)

import numpy as np
points = np.array([129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5,7.5,141.5,23,
147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5]).reshape(14,2)  
#这是给定数据的(xi, yi)，只是先输入了全部x又输入了全部y
values = np.array([-4,-8,-6,-8,-6,-8,-8,-9,-9,-8,-8,-9,-4,-9])  #这是给定数据的zi
 
grid_x, grid_y = np.mgrid[0:200:400j, -100:200:600j] #这是插值点的(xi,yi)
from scipy.interpolate import griddata            #这是求插值点的zi
grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear')
grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic')
 
#下面是绘图
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
plt.figure()
 
ax1 = plt.subplot2grid((2,2), (0,0), projection='3d')
ax1.plot_surface(grid_x, grid_y, grid_z0, color = "c")
ax1.set_title('nearest')
 
ax2 = plt.subplot2grid((2,2), (0,1), projection='3d')
ax2.plot_surface(grid_x, grid_y, grid_z1, color = "c")
ax2.set_title('linear')
 
ax3 = plt.subplot2grid((2,2), (1,0), projection='3d')
ax3.plot_surface(grid_x, grid_y, grid_z2, color = "r")
ax3.set_title('cubic')
 
ax4 = plt.subplot2grid((2,2), (1,1), projection='3d')
ax4.scatter(points[:,0], points[:,1], values,  c= "b")
ax4.set_title('org_points')
 
plt.tight_layout()
plt.show()

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可