目录

1、决策树是一种树模型

2、决策树的训练与测试

3、信息增益（ID3）

3.1、衡量标准-熵

3.2、决策树构造实例

4、决策树算法

​5、连续值离散化

6、预剪枝

---

1、决策树是一种树模型：

（1）、从根结点开始一步步走到叶子结点（决策）

（2）、所有的数据最终都会落到叶子结点，既可以做分类问题也可以做回归问题（分类中使用熵值构建决策树，回归中选择使用方差构建决策树）

2、决策树的训练与测试

（1）、训练阶段：从给定的训练集中构造出一棵树（从根结点开始选择特征，如何进行特征切分）

（2）、测试阶段：根据构造出来的树模型从上到下走一遍就好了

（3）、一旦构造好了绝二叉树，那么分类或者预测问题就很简单，只需要走一遍即可，难点是如何构造出一棵树模型。方法是通过一种衡量标准，来计算通过不同特征进行分支选择后的分类情况，找出来最好的那个当成根节点，以此类推

3、信息增益（ID3）

3.1、衡量标准-熵

（1）、熵：熵表示随机变量不确定性的度量。它表示物体内部的混乱程度，越混乱熵值越大，反之熵值越小。比如国内要是全是咱中国人，那就是熵值很低。但是若是随着国际化程度越来越高，更多的黑人、白人来中国发展、定居，那么此时国内的熵值就特别高。

（2）、计算信息熵公式，对每一个类别的概率pi取对数然后求和。概率pi取值范围为[0,1],所以概率越大信息熵越接近为0。信息熵的计算公式中取负号是因为pi在[0,1]的取值范围内，若是没有负号H(X)取对数结果为负，所以加一个符号让它的结果始终为正。

（3）、使用信息增益建立树模型

3.2、决策树构造实例

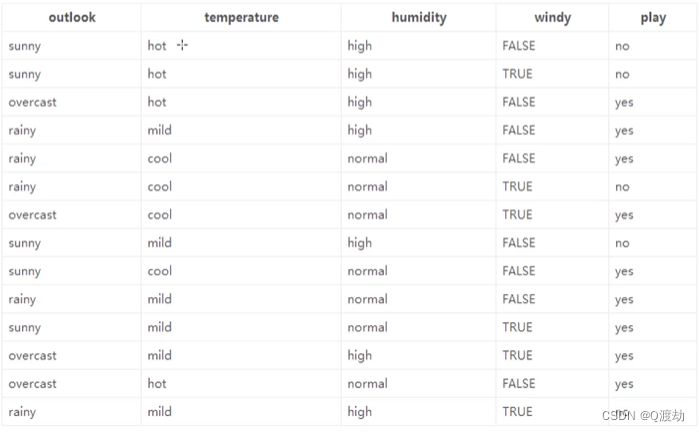
从上面图中可以看出， 根节点的选择有四种情况：基于天气、基于温度、基于湿度、基于是否有风

 

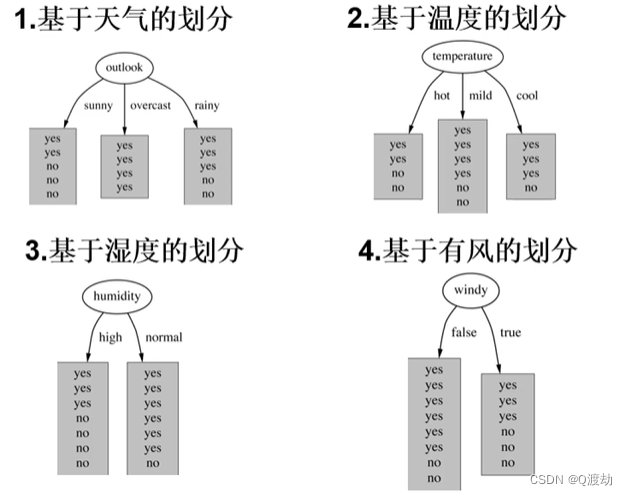
 （1）、首先在历史数据（14天）中有 9 天在打球，5 天不打球，所以此时的熵应该为：

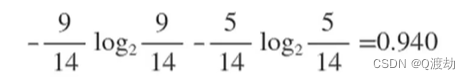
（2）、对四个特征进行逐一分析，首先选择基于天气outlook如下：

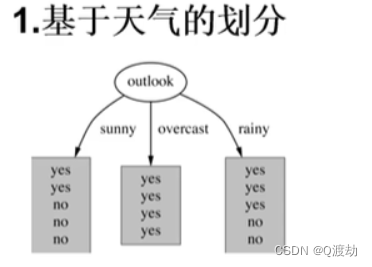
当outlook = sunny时，熵值为 H(x) = -(2/5*log2/5 + 3/5*log3/5) = 0.971

当outlook = overcast时，因为全是yes，所以熵值为 H(x) = -(5/5*log5/5) = 0

当outlook = rainy时，熵值为  H(x) = -(2/5*log2/5 + 3/5*log3/5) = 0.971

（3）、根据数据统计，outlook取值分别为sunny，overcast，rainy的概率分别为 5/14，4/14，5/14

outlook的加权信息熵为：

（4）、信息增益：gain(outlook) =  0940 -  0.693 = 0.247

 循环重复上面的（1）、（2）、（3）、（4）步骤 计算基于温度、基于湿度、基于是否有风这三个特征。下面是其余三个特征的信息增益

 很明显outlook的信息增益最大（从历史信息熵到选择outlook得到的加权信息熵，纯度越来越高），所以根节点选择 outlook特征，如下图

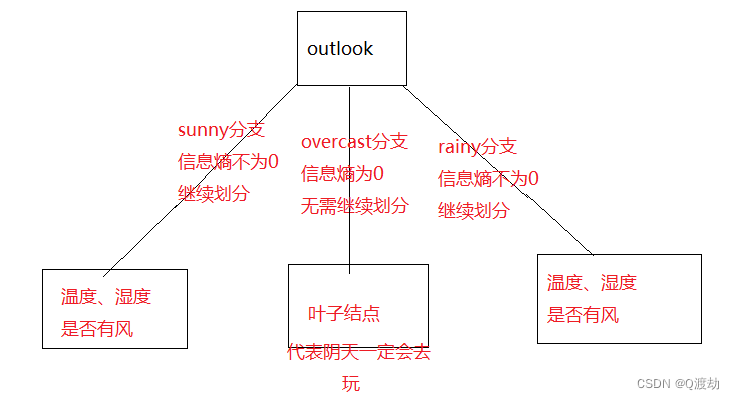
所以下一步直接从sunny和rainy开始

以sunny为例。又以sunny为前提，求sunny对应的信息熵，作为历史信息熵

然后在此前提下按照前面的步骤计算基于温度、基于湿度、基于是否有风的加权信息熵，选择增益信息最大的即为sunny分支对应的根节点（也就是sunny信息熵和它们各自的加权信息熵之差，加权信息熵越小，增益信息越大，也即发生的概率越大）

对rainy执行和sunny同样的操作即可

按照上面的步骤直到每一个分支都是信息熵为0，即要么一定去，要么一定不去，而不会出现两者的混合情况

基于基尼方法构建决策树的过程也是这样，唯一不同的是使用的计算方法不同，为Gini = 1 - (x/n)^2 - (y/n)^2，然后直接选择基尼加权值最小的即可，具体python代码实现过程点击下方连接即可

https://blog.csdn.net/qq_51691366/article/details/130836272?spm=1001.2014.3001.5501

4、决策树算法

ID3：信息增益

C4.5：（解决ID3问题，考虑自身信息熵）信息增益率，用来解决信息增益可能会偏向于选择具有更多取值的特征的问题。信息增益率越大，表示使用该特征来划分样本集合后，对样本分类的影响相对于特征本身的取值数量更大。信息增益和信息增益率都是用来选择最优特征的指标，但信息增益率能更好地处理特征取值数量不同的情况（比如在上面的例子要是再加入一个特征ID，编号从1—14开始，但是经过计算，这个特征的每一个分支的信息熵都是为H(X) = 1/1*log1 = 0，加权信息熵为 0，所以我们就要选择这个特征作为根节点吗？很显然不能，所以这个时候就要使用信息增益率C4.5算法来解决ID3存在的问题，考虑自身信息熵，避免了ID3算法中存在的对取值较多的特征有偏好的情况，提高了决策树分类器的泛化性能。信息增益率越大表示该特征对于划分数据集具有更好的区分能力）

计算公式为 gain(A) / splitInfo(A)，分子表示使用特征A作为划分依据时的信息增益，分母slitInfo(A)表示特征A的分裂信息，定义为所有特征A的取值对样本集合的信息熵的平均值，计算公式如下： splitInfo(A) = - sum(p(i) * log2(p(i))) 其中，p(i)是特征A的第i个取值在样本集合中出现的概率。 在实际应用中，为了避免分母为0的情况，可以对分裂信息加上一个小的常数，例如0.1

CART：使用GINI系数来当做衡量标准，它是一种常用的决策树算法，可以用于分类和回归问题。CART算法与其他决策树算法不同的是，可以处理数值型属性，而不仅仅是离散型属性

GINI系数（基尼方法，具体实现方法看上面的链接），和熵值一样，越小效果越好

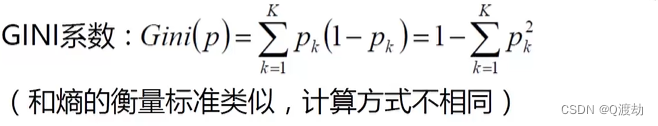5、连续值离散化

首先拿到一个乱序数组，对其进行排序

 然后对排序完之后的每两个数据之间进行二分划分

比如在60到70之间划分，划分点即为65.5，所以以65.5为中间点将上面已经排好序的数组划分为两组，即

 循环进行二分就会得到9个分界点，然后对每一个分界点计算，选取熵值最小，而信息增益最大的分界点即可。这个过程就是连续值离散化的过程。同样在链接https://blog.csdn.net/qq_51691366/article/details/130836272?spm=1001.2014.3001.5501

中对于连续数值离散化的过程就是使用这种方法实现的

6、预剪枝

为什么要进行剪枝：避免出现过拟合问题（指的是模型在训练集上表现良好，但在测试集或新数据上表现不佳的现象），提高模型的泛化能力

解决方法：预剪枝和后剪枝

预剪枝：一边建立决策树，一边建立进行剪枝的操作（更实用），通过限制树的深度、叶子结点个数、叶子结点样本数和信息增益等

后剪枝：决策树建立完成之后进行剪枝的操作，通过一定的衡量标准，叶子结点越多，损失越大

，其中C(T)是熵值乘样本数量，表示叶子结点个数

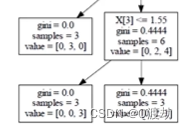
 比如对于为 0.44 * 6 + 1a

而要是的两个叶子结点则为 0*3 + 1a + 0.4444 * 3 + 1a

所以人为设置a的数值，比较前后剪枝完的结果，看看损失的情况，损失程度要是很高，就不进行后剪枝，要是很低就可以进行后剪枝