红黑树复习

图
图,是一种数据结构
集合只有同属于一个集合;线性结构存在一对一的关系,树形结构一对多的关系,图形结构,多对多的关系。
微信中:许多的用户组成了一个多对多的朋友关系网,这个关系网就是数据结构当中的图(Graph)。
导航的最优路径:耗时最少,路程最短的路径,推荐一个方便最快捷的路线。其实就把经过的地方看作图上的一个一个的点,从起点出发,与另外的一个点或者其他的点产生了关联。
图的概念
图:是一种比树更为复杂的数据结构。树结点之间是一对多的关系,并且存在着一个父与子的层级划分。多对多的关系,并且的,所有的顶点都是平等的,无所谓谁是父亲,谁是儿子。
在图中,最基本的单元是顶点(vertex),顶点相当于树中的结点。
顶点之间的关系被称为边(edge)。
图的分类
按照连接的两个顶点的边的不同,可以把图分为以下几种:
- 无向图:边没有方向的图称为无向图,边的作用仅仅是连接两个顶点,没有其他的含义
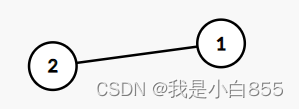
- 有向图:边不仅连接两个顶点,并且具有方向性,可能是单向也可能是双向的
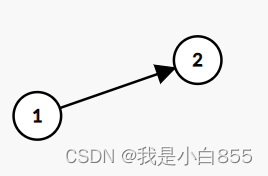
- 带权图:边可以带权重
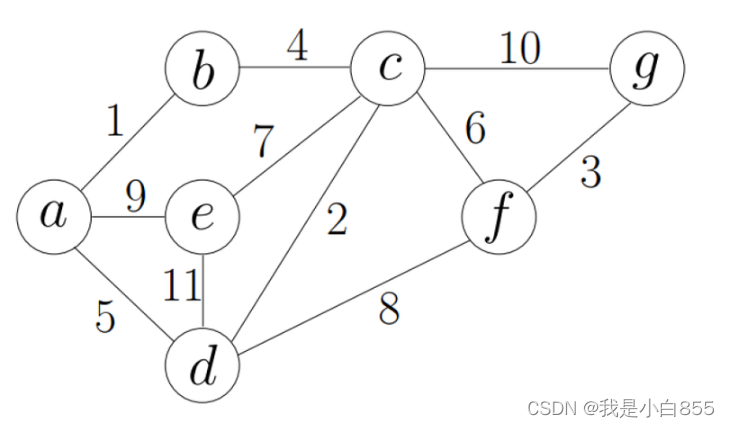
图的术语
- 相邻顶点:当两个顶点通过一条边相连时,我们称这两个顶点是相连的,并且是依附于这两个顶点的。
- 度:某个顶点的度:是依附于这个顶点的边的个数 (树结点的度:结点所拥有的子树的个数;树的度:书中结点度最大值)
- 子图:一幅图中,所有边的子集组成的图,包含这些边的依附的顶点
- 路径:是由边顺序连接的一系列的顶点组成
- 环:是一条至少含有一条边且终点和起点相同的路径
- 连通图:在无向图中,从任意一个结点出发都能到达任意一个结点,那么这副图我们就称之为连通图
- 强连通图:在有向图中,从任意一个结点出发都能到达任意一个结点,那么称该有向图为强连通图。
- 连通子图:一个非连通图由若干个连通的部分组成,每一个连通的部分就可以称为:该图的连通子图(在无向图中,如果删除这个图的一些边(删除的边数>=0),剩下的部分仍然是连通的,那么称这个图是原图的连通子图。)
- 强连通子图:在有向图中,如果删除这个图中的一些边(删除的边数>=0),剩下的部分仍然是连通的,那么称这个图是原图的强连通子图。
- 极大连通子图:如果无向图的连通子图包含它的原图中所有与它自身有关的边,那么称它为极大连通子图。
- 极大强连通子图:如果有向图的连通子图包含它的原图中所有与它自身有关的边,那么称它为极大强连通子图。
- 极小连通子图:如果删除无向图的连通子图的任意一条边都会导致该子图不再连通,那么称这个子图为极小连通分量。
- 极小强连通子图:如果删除有向图的连通子图的任意一条边都会导致该子图不再连通,那么称这个子图为极小强连通子图。
- 连通分量:无向图的极大连通子图为该图的连通分量。
- 强连通分量:有向图的极大强连通子图为该图的强连通分量。
- 弱连通图:将有向图的所有的有向边替换为无向边,所得到的图称为原图的基图。如果一个有向图的基图是连通图,则该有向图是弱连通图。
欧拉七桥
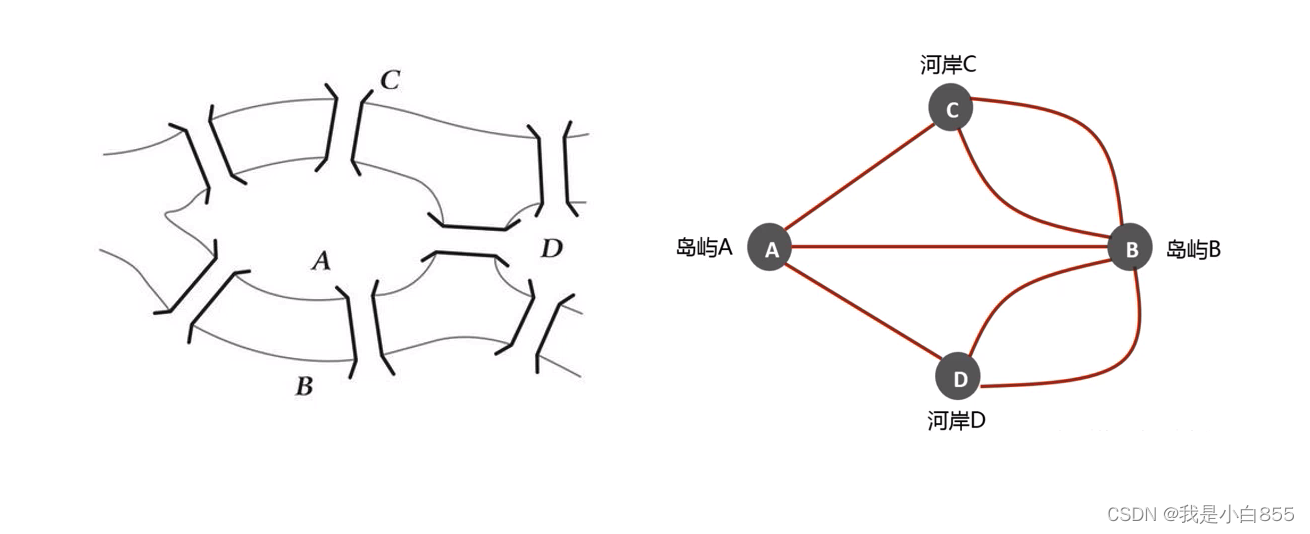
每个桥走一次,回到出发点 ->办不到
欧拉得出结论,创建图论
图的存储结构
- 顺序存储
- 链式存储
线性表:它仅有的关系就是线性关系
树形结构:有清晰的层次的结构
图形结构:集合中的每一个元素都有可能有关系
图是由顶点和边构成。所以在图里边:要存储的图形结构的信息,无非就是存储图的顶点和图的边。
顶点存储
顶点可以直接用数组去存储
例如:
1,2,3,4=>[1,2,3,4]
A,B, C, D =>[A ,B ,C ,D]
边的存储
- 邻接矩阵
用一个一维数组存放图中所有顶点数据;用一个二维数组存放顶点间关系(边或弧)的数据,这个二维数组称为邻接矩阵。邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵
矩阵是一个按照长方阵列排列的负数或者实数集合。
N* M 数据的集合
去除表格线的九宫格就是矩阵的样式。矩阵是由行和列组成的一组数表。
邻接矩阵让每一个结点和整数相关联
用1表示顶点与顶点有直接的关系,用0表示没有连接
优点:表示非常的明确,有向图:A->D:1 D->A 0
缺点:非常浪费计算机的内存。存储了太多0,
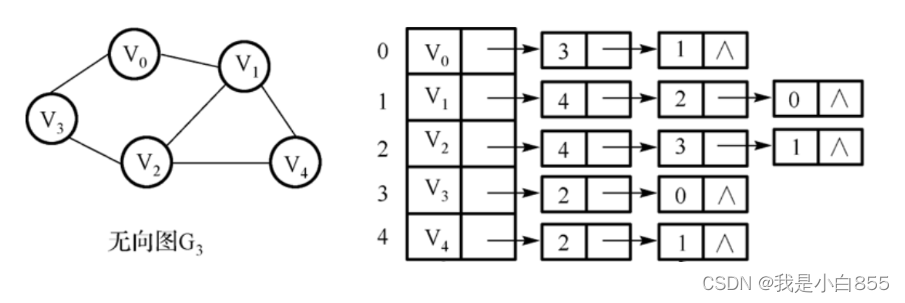
无向图
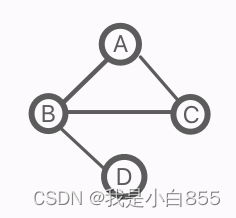
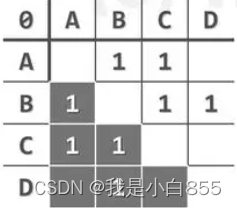
对称
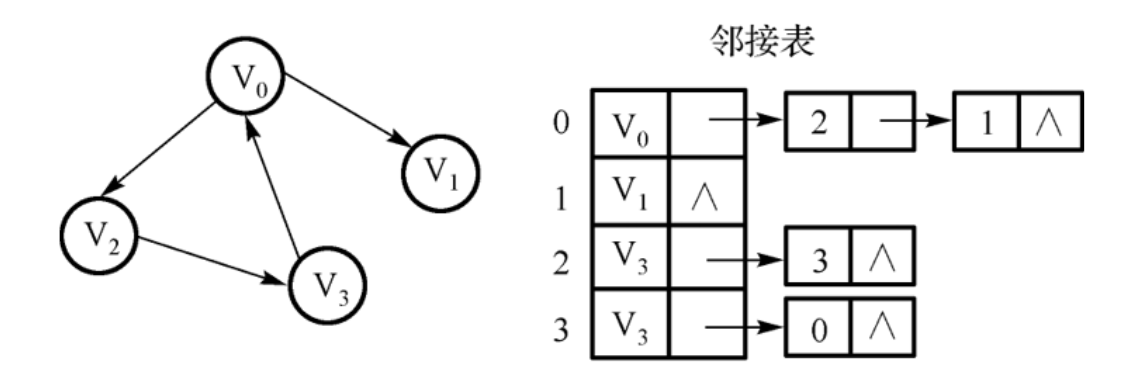
有向图
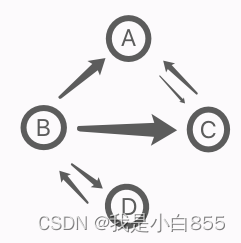
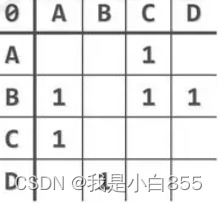
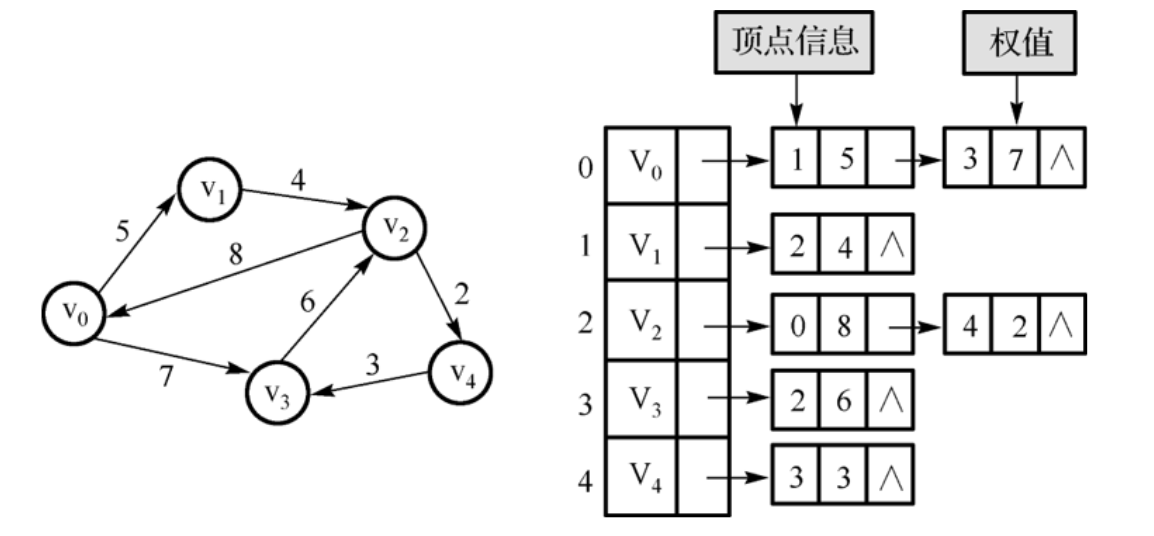
带权图


- 邻接表
邻接表:由图中的每个顶点以及和顶点相邻的顶点列表组成。数组/链表
存储方法跟树的孩子链表示法相类似,是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点,则把相邻顶点依次存放于表头结点所指向的单向链表中。
20172311《程序设计与数据结构》第九周学习总结 - socialsea - 博客园