在阅读本文前,请确保你已经掌握代价函数、假设函数等常用机器学习术语,最好已经学习线性回归算法,前情提要可参考https://blog.csdn.net/weixin_45434953/article/details/130593910
分类问题是十分广泛的一个问题,其代表问题是:
- 一个邮件是否为垃圾邮件
- 一个肿瘤是否为恶性肿瘤
我们通常用y来表示分类结果,其中最简单y值集合为
0
,
1
{0,1}
0,1,比如对于一个邮件是否为垃圾邮件,有“是垃圾邮件(1)”和“不是垃圾邮件(0)”两种y的取值。假设以肿瘤大小为x轴,是否为恶性肿瘤为y轴,并且有如下一个数据集:

很显然,这个数据集合是无法使用之前学习的线性回归集合进行拟合的。因为一旦将直线延长,就会出现一个大概率是恶性肿瘤的数据被判定为良性,如下图所示

要解决这个问题,可以使用logistic回归算法,下面我们将会学习这个算法。
Logistic回归算法
作为一个回归算法,Logistics回归算法当然也有假设函数
h
θ
(
x
)
=
θ
T
x
h_\theta(x)=\theta^Tx
hθ(x)=θTx(其中x是一个向量),我们将数据集输入到x中,最后会输出个预测结果y。当然,由于我们要解决的是分类问题,如上面分析所示,我们的
h
θ
(
x
)
h_\theta(x)
hθ(x)的取值应该是位于
[
0
,
1
]
[0,1]
[0,1]之间,而传统的
h
θ
(
x
)
h_\theta(x)
hθ(x)函数的取值范围是整个实数域,因此我们要改造下
h
θ
(
x
)
h_\theta(x)
hθ(x)函数,让他的取值范围落在
[
0
,
1
]
[0,1]
[0,1]之间。因此我们定义Logistic回归算法的
h
θ
(
x
)
h_\theta(x)
hθ(x)函数如下所示:
h
θ
(
x
)
=
g
(
θ
T
x
)
(1)
h_\theta (x)=g(\theta^T x)\tag{1}
hθ(x)=g(θTx)(1)
g
(
z
)
=
1
1
+
e
−
z
(2)
g(z)=\frac{1}{1+e^{-z}}\tag{2}
g(z)=1+e−z1(2)上面的2式被称之为Logistic函数,或者称为Sigmoid函数。该函数的图像如下:
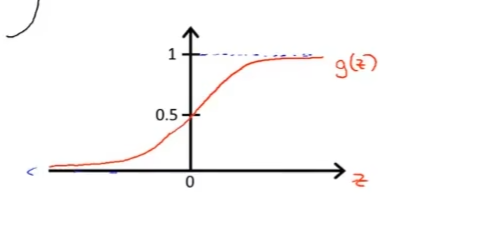
对于
z
∈
R
z\in R
z∈R,Logistics函数的取值范围是
[
0
,
1
]
[0,1]
[0,1],因此,将(1)(2)结合起来可以得到
h
θ
(
x
)
=
1
1
+
e
−
θ
T
x
h_\theta(x)=\frac{1}{1+e^{-\theta^T x}}
hθ(x)=1+e−θTx1该函数的取值范围为[0,1]
我们需要做的,和之前线性回归一样,就是选定合适的参数 θ \theta θ来拟合我们的数据,从而在输入一定特征x的时候,可以获得正确的输出结果y。我们知道分类问题的结果一般只有0或1,而假设函数 h θ ( x ) h_\theta(x) hθ(x)的结果则代表着在输入特征为x的情况下,y=1的概率是多少,比如说,向量 x 0 x_0 x0代表着0号肿瘤的所有特征, h θ ( x 0 ) = 0.7 h_\theta(x_0)=0.7 hθ(x0)=0.7也就意味着该肿瘤为恶行的几率为0.7。
决策界限
那么当 h θ ( x ) h_\theta(x) hθ(x)等于多少的时候,我们会认为y=1呢?一个最简单的办法就是:当 h θ ( x ) ≥ 0.5 h_\theta(x)\geq 0.5 hθ(x)≥0.5的时候,我们认为当前情况下y=1;当 h θ ( x ) < 0.5 h_\theta(x)<0.5 hθ(x)<0.5的时候,我们认为y=0。我们再观察回Logistics函数,可以发现,当 z ≥ 0 z\geq0 z≥0的时候 h θ ( x ) ≥ 0.5 h_\theta(x)\geq 0.5 hθ(x)≥0.5,也就是当 θ T x ≥ 0 \theta^T x\geq0 θTx≥0。
现在假设我们有如下的数据集,并且假设函数
h
θ
(
x
)
h_\theta(x)
hθ(x)如下:
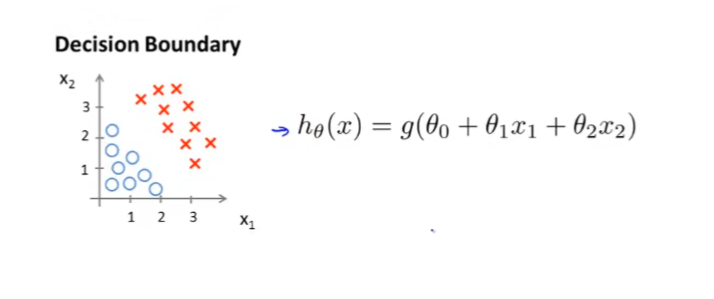
我们假设
θ
0
=
−
3
,
θ
1
=
1
,
θ
2
=
1
\theta_0=-3, \theta_1=1, \theta_2=1
θ0=−3,θ1=1,θ2=1,那么我们可以在数据集上画出这样的一条线:
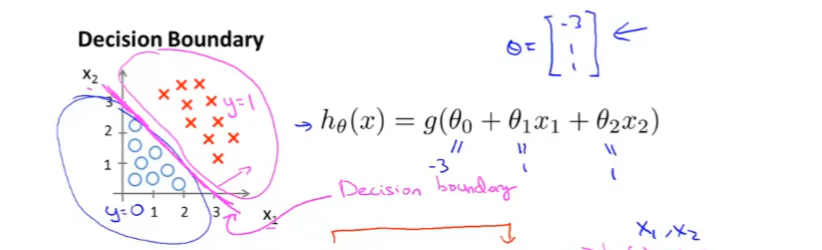
这将平面分为了两部分,其中在直线之下的会使得
h
θ
(
x
)
<
0.5
h_\theta(x)<0.5
hθ(x)<0.5,我们会估计落在这部分的数据y=0。这一条切分平面的直线,我们称之为决策边界
Logistic下的代价函数
接下来我们需要分析Logistics回归算法的代价函数,让我们来复习下,代价函数主要是用来衡量算法输出结果和实际的正确值的拟合程度,代价函数
J
(
θ
)
J(\theta)
J(θ)主要作用就是找到合适的
θ
\theta
θ值,使得代价函数
J
(
θ
)
J(\theta)
J(θ)最小,从而使得算法拟合效果最优。 一般的代价函数表达式如下:
J
(
θ
)
=
1
m
∑
i
=
1
n
1
2
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
)
J(\theta)=\frac{1}{m}\sum_{i=1}^n\frac{1}{2}Cost(h_\theta(x^{(i)}),y)
J(θ)=m1i=1∑n21Cost(hθ(x(i)),y)我们之前学习的线性回归算法的Cost函数为
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
)
=
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
Cost(h_\theta(x^{(i)}),y) = (h_\theta(x_{(i)})-y_{(i)})^2
Cost(hθ(x(i)),y)=(hθ(x(i))−y(i))2但是如果在Logistics中使用这种Cost函数会导致代价函数为一个非凸函数,这主要是因为Logistics的假设函数
h
θ
(
x
)
h_\theta(x)
hθ(x)中含有指数项的原因,在这不展开阐述,总之,其函数可能会类似于下图的形状。
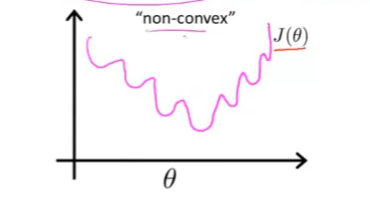
可以看到上面有很多的局部最优值,如果使用梯度下降函数,它在大多数情况是无法拟合到最优值的。那么我们的需求就很清晰了,我们希望可以找到一个Cost函数,可以使得
J
(
θ
)
J(\theta)
J(θ)的函数是一个凸函数,或者单弓型函数。那么实际上,他的Cost函数如下:
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
)
=
{
−
l
o
g
(
h
θ
(
x
)
)
i
f
y
=
1
−
l
o
g
(
1
−
h
θ
(
x
)
)
i
f
y
=
0
\begin{equation} Cost(h_\theta(x^{(i)}),y) = \begin{cases} -log(h_\theta(x))& if\: y=1\\ -log(1-h_\theta(x))& if\: y=0\\ \end{cases} \end{equation}
Cost(hθ(x(i)),y)={−log(hθ(x))−log(1−hθ(x))ify=1ify=0
看起来式子十分复杂,但是容我仔细分析下:上文提到,h(x)代表的是算法认为y=1的概率是多少,并且
h
(
x
)
∈
[
0
,
1
]
h(x)\in [0,1]
h(x)∈[0,1],那么当y=1的时候,Cost曲线如下图所示:

当h(x)越接近1,Cost函数的值越接近0,这样得出来的代价函数也越小。也就是在真实结果y=1的情况下,如果h(x)=1,也就是函数认为该实例一定为1,证明它完全预测成功了,那么Cost=0,最终得出的代价函数也会非常小,即使h(x)=0.9,也就是函数认为有90%的概率该实例为1,那Cost的值还不到0.05,最终代价函数的增加幅度也很小,因为它确实也大概率预测成功了。如果他对于一个y=1的实例预测值为0,也就是他认为该实例不可能为1,那么Cost函数将会狠狠地"惩罚"这个学习算法,Cost的值会直接趋于无穷大,从而导致代价函数也无穷大,很明显,这是一个很糟糕的
θ
\theta
θ取值
反之,如果y=0的时候其函数图像如下:

很显然,这和上面刚好相反。举一反三即可。
代价函数的简化和梯度下降
上面的Logistics代价函数可以总结为两个式子:
J
(
θ
)
=
1
m
∑
i
=
1
n
1
2
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
)
(1)
J(\theta)=\frac{1}{m}\sum_{i=1}^n\frac{1}{2}Cost(h_\theta(x^{(i)}),y)\tag{1}
J(θ)=m1i=1∑n21Cost(hθ(x(i)),y)(1)
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
)
=
{
−
l
o
g
(
h
θ
(
x
)
)
i
f
y
=
1
−
l
o
g
(
1
−
h
θ
(
x
)
)
i
f
y
=
0
(2)
\begin{equation} Cost(h_\theta(x^{(i)}),y) = \begin{cases} -log(h_\theta(x))& if\: y=1\\ -log(1-h_\theta(x))& if\: y=0\\ \end{cases} \end{equation}\tag{2}
Cost(hθ(x(i)),y)={−log(hθ(x))−log(1−hθ(x))ify=1ify=0(2)
当然,由于y只有等于1或者等于0两种取值,我们可以将2式简化为如下形式:
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
)
=
−
y
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
l
o
g
(
1
−
h
θ
(
x
)
)
(3)
Cost(h_\theta(x^{(i)}),y)=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))\tag{3}
Cost(hθ(x(i)),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))(3)观察可以知道,3式和2式是等价的。
将他们合起来就得到了代价函数 J ( θ ) J(\theta) J(θ) J ( θ ) = 1 m ∑ i = 1 n 1 2 [ − y l o g ( h θ ( x ) ) − ( 1 − y ) l o g ( 1 − h θ ( x ) ) ] J(\theta)=\frac{1}{m}\sum_{i=1}^n\frac{1}{2}[-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))] J(θ)=m1i=1∑n21[−ylog(hθ(x))−(1−y)log(1−hθ(x))]
求得最小代价函数的任务自然就交给了梯度下降算法,对于每一个变量 θ j \theta_j θj反复采取以下式子处理: θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j := \theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta) θj:=θj−α∂θj∂J(θ)另外我们已经知道 J ( θ ) J(\theta) J(θ),对导数进行计算可以得出 ∂ ∂ θ j J ( θ ) = 1 m ∑ i = 1 n ( h θ ( x ( i ) − y ( i ) ) x j ( i ) \frac{\partial}{\partial\theta_j}J(\theta)=\frac{1}{m}\sum_{i=1}^n(h_\theta(x^{(i)}-y{(i)})x_j^{(i)} ∂θj∂J(θ)=m1i=1∑n(hθ(x(i)−y(i))xj(i)则可以得出梯度下降的实际函数为 θ j : = θ j − α 1 m ∑ i = 1 n ( h θ ( x ( i ) − y ( i ) ) x j ( i ) \theta_j := \theta_j-\alpha\frac{1}{m}\sum_{i=1}^n(h_\theta(x^{(i)}-y{(i)})x_j^{(i)} θj:=θj−αm1i=1∑n(hθ(x(i)−y(i))xj(i)由于我们的代价函数已经是一个凹函数了,那梯度下降是可以得到最优值的。上述的例子中,为了方便理解, θ \theta θ中只有一个值,一个数据实例中也只有一个特征x来用于预测y的取值,实际上运用的时候, θ \theta θ可以是一个含有多个元素的向量,当数据集给出若干个特征 x i x_i xi的时候,可以用Logistics来进行拟合
之前我们介绍了二元分类问题,但是现实的很多分类问题并非是只需要将某一事物分类成两类,而是要划分为好多种类别。比如天气预报需要根据天气数据,将天气大致分为晴天、阴天、下雨、下雪等若干类别。下面我们开始介绍一对多分类问题的基本原理。
多元分类问题

假设我们需要将数据集中的数据分为三类:正方形、三角形和叉。那么我们采取的做法是,将正方形和叉视作一类,将三角形分离出来,然后将三角形和叉视作一类,使用一个二元分类算法将正方形分离出来,再将三角形和正方形视作一类,将叉分离出来。
上述的做法使用了3次二元分类算法,最终将三个类别分离了出来。