在阅读本文前，强烈建议有志入门群论的同学观看 3blue1brown 魔群 视频。

对于计算机方向同学，可以尝试从数据结构的角度理解。本文主要基于文档、网站 Nauty 和 Nauty 的 python binding, pynauty(github.com) 展开。

Nauty 数据结构

本小节截选自 Nauty 文档。上文提到，我们通过将三维的分子结构转换为一维数组来进行群的作用。如下图所示：

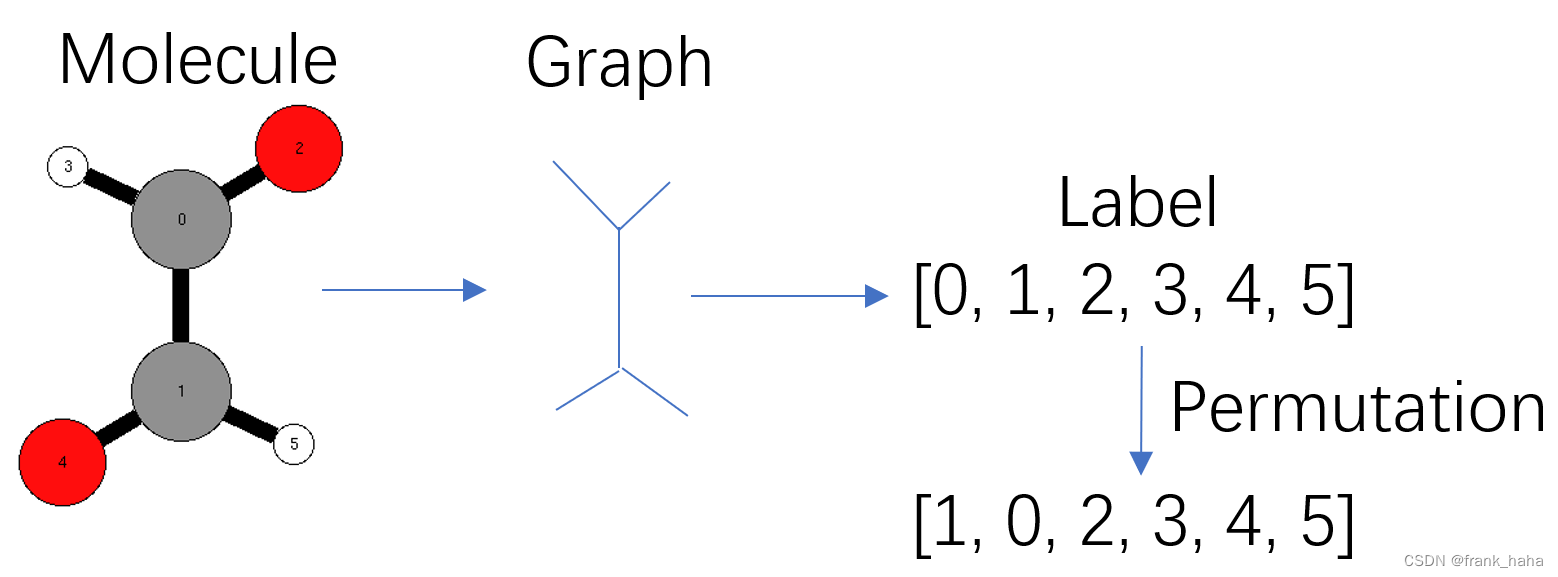
之所以从数据结构角度理解，是因为 Nauty 的数据结构是一维的，更符合程序员思维，涉及抽象符号较少。下面我们关注其中涉及到的群操作。

交换

交换是一种群的作用（Action），一串数组中，通过更换几个数字的位置，可以得到新的数组。如下图所示：

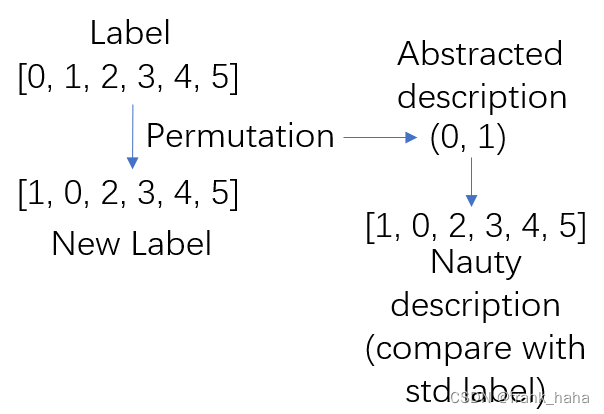
交换前后，新标签和旧标签对比，可以得到交换的位点。本例中，如果使用抽象语言，这种群作用通过 (0,1) 表示。Nauty 通过将这种群作用施加在标准数组上，得到能够代表这种群作用的数组。

上例混淆了起始数组和标准数组，可看下例：

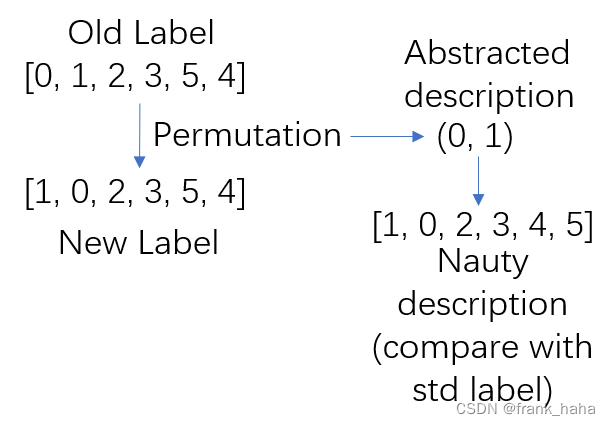
这种形式能够将群作用结构化，他们都有着特定的数组长度。Nauty 文档里举了一个更加复杂的例子：

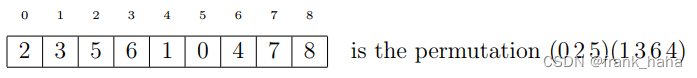
是从 Nauty description 倒推 Abstracted description.

我们可以看到，和标准数组相比 0, 2, 5 和 1, 3, 6, 4 的位置是混乱的两组，但是 7,8 没有变，所以 7, 8 没有在抽象描述中显现。

自同构群

上小节介绍了交换作用的数据结构，但脱离了图的语境。

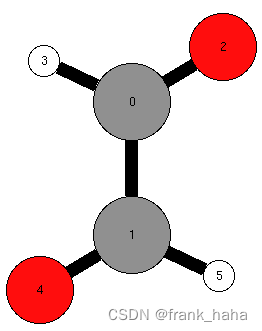
我们再回看该分子图。一种交换，比如说 1, 0, 2, 3, 4, 5 ，代表着交换 0, 1 两个碳原子交换。从化学角度看，我们认为这种交换并不改变分子结构。如果使用群论的术语，我们说 1, 0, 2, 3, 4, 5 是一种自同构群。（严谨的说，是自同构群作用，一个图的自同构群包含了所有类似的群作用）注意，并不是所有的群作用都是自同构群，只有交换前后结构不变的群作用可以叫做自同构群。比如， 2, 1, 0, 3, 4, 5 表示 0, 2 交换，显然会改变分子结构，因此， 2, 1, 0, 3, 4, 5 只是一种群作用而不是自同构群。（其实这里表述仍然不严谨，但可以这样理解）

轨道

轨道二字会让人联想到 “行星轨道” ，“原子轨道” 等。在 “原子轨道” 里，电子和原子核间的相互作用简化为了电子围绕原子核转动，同一轨道上的电子能量相同，后来这种思想延续到了分子轨道中 “简并轨道” 概念里。

群论语境下，轨道也有类似的含义。同一轨道的元素 (element) 互相交换，结构不变。以下面分子图为例：

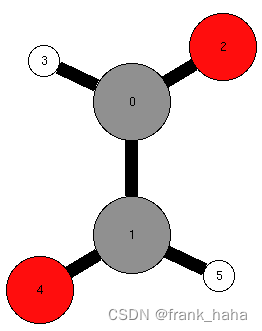
我们可以说 0, 1 处于同一轨道，因为交换二者不会带来结构的变化。群论里，我们用 {0, 1}, {3, 5}, {2, 4} 来表述轨道。

Nauty 使用一个数组来存储轨道信息：

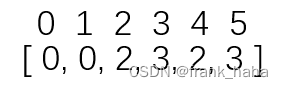
同一轨道中，数值最小的元素代表整个轨道。比如：{2, 4} 对应位置由 2 来代替。

下面是 Nauty 手册给的一个例子，可做练习：

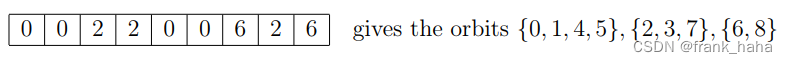
染色

分子图的染色很好理解，不同的点代表不同的原子。我们这里仅讨论点的染色。下图是 ASE 渲染的分子图：

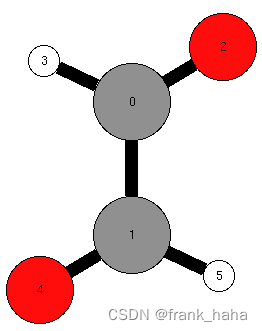
Nauty 使用两个数组来表示一种染色方案，分别是 lab 和 ptn.

lab 是变动较大的，没有太多含义。我们这里按照 CHO 的顺序排列。

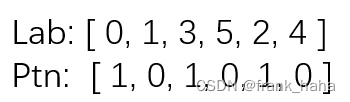
ptn 中 1 表示对应位点和后面一位位点的颜色相同，0 表示对应位点和后面一位位点颜色不同。所以 101010 表示 {0, 1}, {3, 5}, {2, 4} 三种颜色。注意，染色和轨道是不同的概念。染色通常作为试错的手段，探索自同构群，比如，目前最快的图同构算法就是通过染色实现的。而轨道是图的固有性质，是固定不变的，需要被求解的。

Nauty 手册给了一个染色的例子，可做练习：

值得注意的是，此处的 1 可以替换为其他数值，比如下面的染色和上面一致：

Nauty 的搜索树

上一章节介绍了群论相关的专业术语。下面我们以 Nauty 网站上介绍的 搜索树 为例，综合运用这些术语。开始之前，我们首先介绍一下图的自同构问题 （graph isomorphism problem）

图的自同构问题

图的自同构问题，旨在判断两个图是否一致。如下图所示：

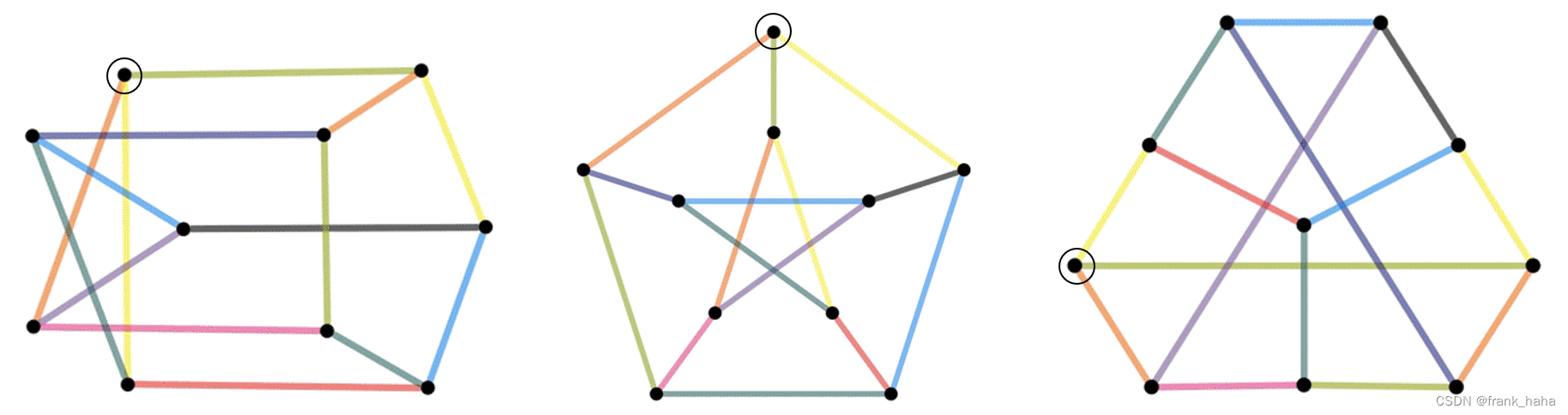
三种图看起来是不一样的，但如果仅考虑拓扑关系，三者每条边、每个顶点都能找到一致的。比如，上图用黑色圈圈起了一个顶点，该顶点连接的三条边的颜色是一致的。（图自目前最快的图同构算法）

图的自同构可以定义为：一张图中的每个点都能在另一张图中找到映射，且点的邻居的颜色一致，和点相连的边的颜色一致。

Nauty 算法起初就是为了解决这一问题而产生的，一个简化版的介绍可以看我之前的博客。

搜索树中的专业术语

在第 7 页 PPT 之前，我们已经通过特定的染色程序得到了两种染色方案。

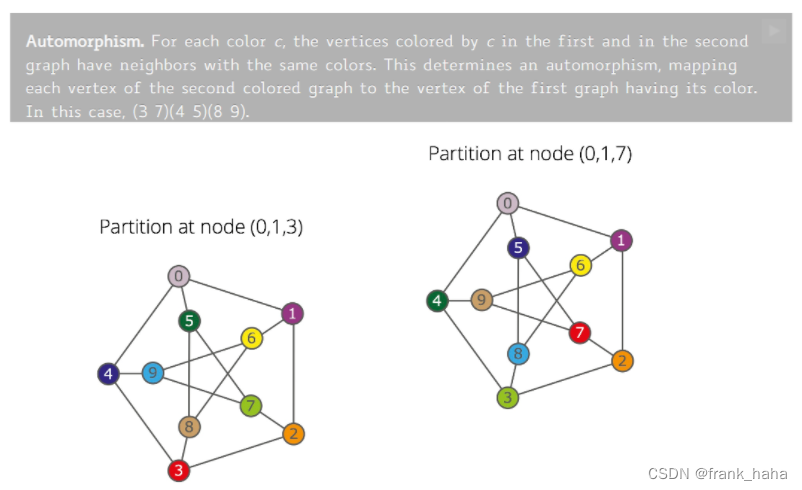
通过对比二者，比如说 3, 7 ，颜色是发生变化的。但变化前后，红色三个邻居的颜色是一致的。所以，我们认为群作用 (3, 7) 是一种自同构的群作用。然而，这种说法并不严谨，因为上图中一共出现了三对类似的群作用。这三对是同时发生的。因此，准确的说法是，(3, 7)(4, 5)(8, 9) 是一种自同构的群作用。

我们用类似的方法得到第二种群作用，与上面得到的一起，产生了一个轨道。

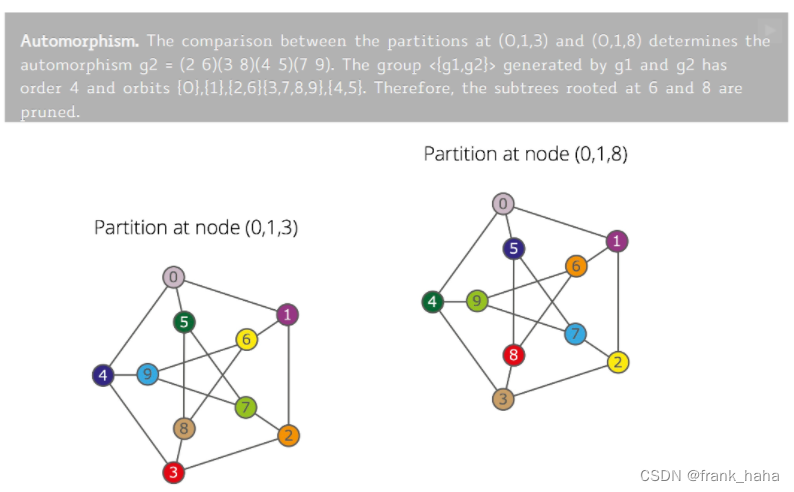
观察轨道和两个群可以发现，轨道的运算可以简单理解为群的交并。

值得注意的是，g1 和 g2 虽然有相同的成分，但由于存在不同的成分，二者并不能相互转化。后续的遍历过程又生成了其他的群（自同构群作用），但颗粒度都较大。群论里，我们称这种最小颗粒度的群为 generator （因为没有其他更小的）。

此外，还有一个常被提到的概念是群的秩。（这里的群指囊括了所有群作用的群）这个数字指，最少自乘多少次可以回到原始状态，反应了一个群的复杂程度。Explain of order

Nauty 里通过两个参数和一个公式来描述一个群的秩：

Pynauty

使用 pynauty(github.com) 可以很好的练习群论知识。

Pynauty 实现了以下主要功能：

1. 给定一个图，返回其自同构群相关信息。
2. 给定两个图，返回二者是否同构。
3. 给定一个图，返回正则化的命名序列。
4. 可以考虑点的特征信息。

下面程序把乙二醛的图信息转化成了 Pynauty 格式，解出了这张图的自同构群信息，给出了正则化命名序列：

from pynauty import *
from ase.build import molecule
from ase.visualize import view
from ase.neighborlist import build_neighbor_list


a_mol = molecule(name='OCHCHO')
neighborlist = build_neighbor_list(a_mol, bothways=False, self_interaction=False)

view(a_mol)

mat = neighborlist.get_connectivity_matrix(sparse=True)

adj_dic = {}
for i in range(len(a_mol)):
    if len(mat[i]) == 0:
        continue
    adj_dic.update({i: list(mat[i].tocoo().col)})

a_g = Graph(number_of_vertices=len(a_mol), directed=False, adjacency_dict=adj_dic)
generators, grpsize1, grpsize2, orbits, numorbits = autgrp(a_g)
lab = canon_label(a_g)

需要注意的是，我们传入的图信息，不包括点和边的特征信息。目前 Pynauty 可以通过染色的方式传入点的特征信息，但不支持边的特征信息录入。此外，Pynauty 仅能在 Linux 和 Mac 平台运行，没有 win 版本。

虽然功能有限，但如果只是使用 Nauty 程序包的核心功能，即解决两图是否同构的问题，Pynauty 不失为一种很好的选择。