wy的leetcode刷题记录_Day56

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间：2022-11-30

前言

895. 最大频率栈

今天的每日一题是：895. 最大频率栈

题目介绍

设计一个类似堆栈的数据结构，将元素推入堆栈，并从堆栈中弹出出现频率最高的元素。

实现 FreqStack 类:

FreqStack() 构造一个空的堆栈。
void push(int val) 将一个整数 val 压入栈顶。
int pop() 删除并返回堆栈中出现频率最高的元素。
如果出现频率最高的元素不只一个，则移除并返回最接近栈顶的元素。

示例 1：输入：[“FreqStack”,“push”,“push”,“push”,“push”,“push”,“push”,“pop”,“pop”,“pop”,“pop”], [[],[5],[7],[5],[7],[4],[5],[],[],[],[]
输出：[null,null,null,null,null,null,null,5,7,5,4]
解释： FreqStack = newFreqStack();
freqStack.push (5);//堆栈为 [5] freqStack.push (7);//堆栈是
[5,7] freqStack.push (5);//堆栈是 [5,7,5] freqStack.push (7);//堆栈是
[5,7,5,7] freqStack.push (4);//堆栈是 [5,7,5,7,4] freqStack.push
(5);//堆栈是 [5,7,5,7,4,5] freqStack.pop ();//返回 5 ，因为 5 出现频率最高。堆栈变成
[5,7,5,7,4]。 freqStack.pop ();//返回 7 ，因为 5 和 7 出现频率最高，但7最接近顶部。堆栈变成
[5,7,5,4]。 freqStack.pop ();//返回 5 ，因为 5 出现频率最高。堆栈变成 [5,7,4]。
freqStack.pop ();//返回 4 ，因为 4, 5 和 7 出现频率最高，但 4 是最接近顶部的。堆栈变成 [5,7]。

思路

根据题目我们需要构建一个类似堆栈的数据结构，不过其pop的值不太一样，pop返回的时当前最接近栈顶的出现频率最高的元素。于是我们选择用俩个哈希表和一个临时变量来保存一些重要数据：1、其中一个表用来保存每一个值出现的频次。2、另一个表用来保存相应出现频次对应的值。3、临时变量用来根据每次更新的值出现的频次中的最大频次。（最近更新的一定是靠近栈顶的）。每次push和pop的时候维护这三个值就可以了。

代码

class FreqStack {
public:
    unordered_map<int,int> hash;
    unordered_map<int,stack<int>> hash_group;
    int maxFrequency;

    FreqStack() {
        maxFrequency=0;
    }
    
    void push(int val) {
        hash[val]++;
        hash_group[hash[val]].push(val);
        maxFrequency=(max(hash[val],maxFrequency));       
    }
    
    int pop() {
        int val=hash_group[maxFrequency].top();
        hash[val]--;
        hash_group[maxFrequency].pop();
        if(hash_group[maxFrequency].empty())
        {
            maxFrequency--;
        }
        return val;
    }
};

/**
 * Your FreqStack object will be instantiated and called as such:
 * FreqStack* obj = new FreqStack();
 * obj->push(val);
 * int param_2 = obj->pop();
 */

收获

简单的构造数据结构题，弄清题意，使用现有的STL来构造对应要求的容器

236. 二叉树的最近公共祖先

题目介绍

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

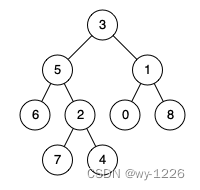
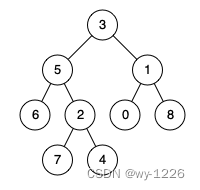
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

思路

方法一：后续遍历：读完题目，我觉得应该采用自底向上的遍历方法来寻找祖先节点，于是想到了后序遍历，递归通路是，当以当前节点为根节点的子树若是包含p或者q，那么将其返回，若是当前节点就是p或者q返回当前节点。考虑到俩个节点可能是一样的，于是当左节点的子树包含p或q，但右节点不包含时，返回左节点，同理右节点。当俩个节点不同时，我们在递归中总有一次能寻找到left和right同时不为空的情况，此时就是最近祖宗节点了。
方法二（看了题解之后的思路）：哈希表存贮父节点：使用一个哈希表来存贮每一个节点的父节点的指向，其中根节点指向空。然后使用另一个哈希表来保存每个节点是否遍历。然后我们直接从第一个哈希表中寻找p或者q，然后一直遍历其父节点直至根节点（空），期间需要将第二个哈希表（维护是否被节点是否被遍历）中的相应节点置为被遍历，就是相当于遍历一条树的通路，此时我们再根据第一个哈希表寻找另一个节点然后也是遍历当出现遍历到的父节点之前被遍历过的时候那么该节点就是题目所求的节点。

代码

后序遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==nullptr)
        {
            return root;
        }
        TreeNode* left=lowestCommonAncestor(root->left,p,q);
        TreeNode* right=lowestCommonAncestor(root->right,p,q);
        if((root==p)||(root==q))
        {
            return root;
        }
        if(left!=NULL&&right!=NULL)
        {
            return root;
        }
        if(left!=NULL&&right==NULL)
            return left;
        else if(right!=NULL&&left==NULL)
            return right;
        else{
            return NULL;
        }

    }
};

哈希表维护：

class Solution {
public:
    unordered_map<int, TreeNode*> fa;
    unordered_map<int, bool> vis;
    void dfs(TreeNode* root){
        if (root->left != nullptr) {
            fa[root->left->val] = root;
            dfs(root->left);
        }
        if (root->right != nullptr) {
            fa[root->right->val] = root;
            dfs(root->right);
        }
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        fa[root->val] = nullptr;
        dfs(root);
        while (p != nullptr) {
            vis[p->val] = true;
            p = fa[p->val];
        }
        while (q != nullptr) {
            if (vis[q->val]) return q;
            q = fa[q->val];
        }
        return nullptr;
    }
};