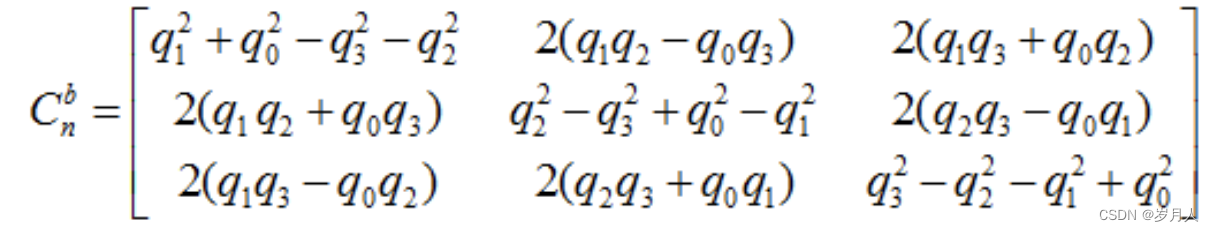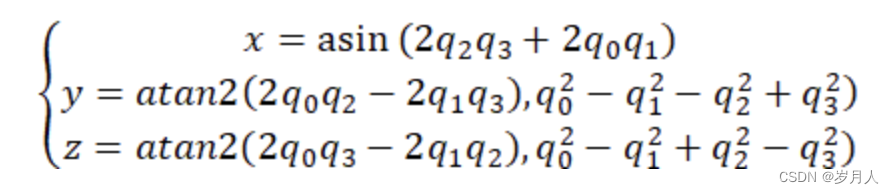理论篇

欧拉角四元数方向余弦矩阵

强调三者描述的是坐标系A,A`之间的变换关系

欧拉角，四元数，方向余弦矩阵都可以描述四轴的姿态变换
注意这里强调的是变换
三者转换公式

一阶龙格库塔法

核心要点简介: 假设一阶函数随时间关系如: y = a * T1+b 则,在经过时间△t后,公式变为y = a * (T1 + △t) + b

由此衍生四元数q在经历△t时间后的新四元数推导公式
【高中数学的一阶求导与多项式之间的关系】

在这里插入图片描述
可得出更新四元数的程序代码为：(其中w为陀螺仪角速度)
q0=q0+(-wxq1-wyq2-wzq3)half_T；
q1=q1+(wxq0+wzq2-wyq3)half_T；
q2=q2+(wyq0-wzq1+wxq3)half_T；
q3=q3+(wzq0+wyq1-wx*q2)*half_T；

总结: 上述的数学定义是我们进行姿态解算的基础理论
通过角速度与时间的积分,在已知四元数初始值,便可以求得△t时间的四元数
通过四元数便可以求得姿态角,同时避免了万向锁问题,从而可以进行全姿态360度飞行控制

6轴IMU(Mahony)姿态融合原理图

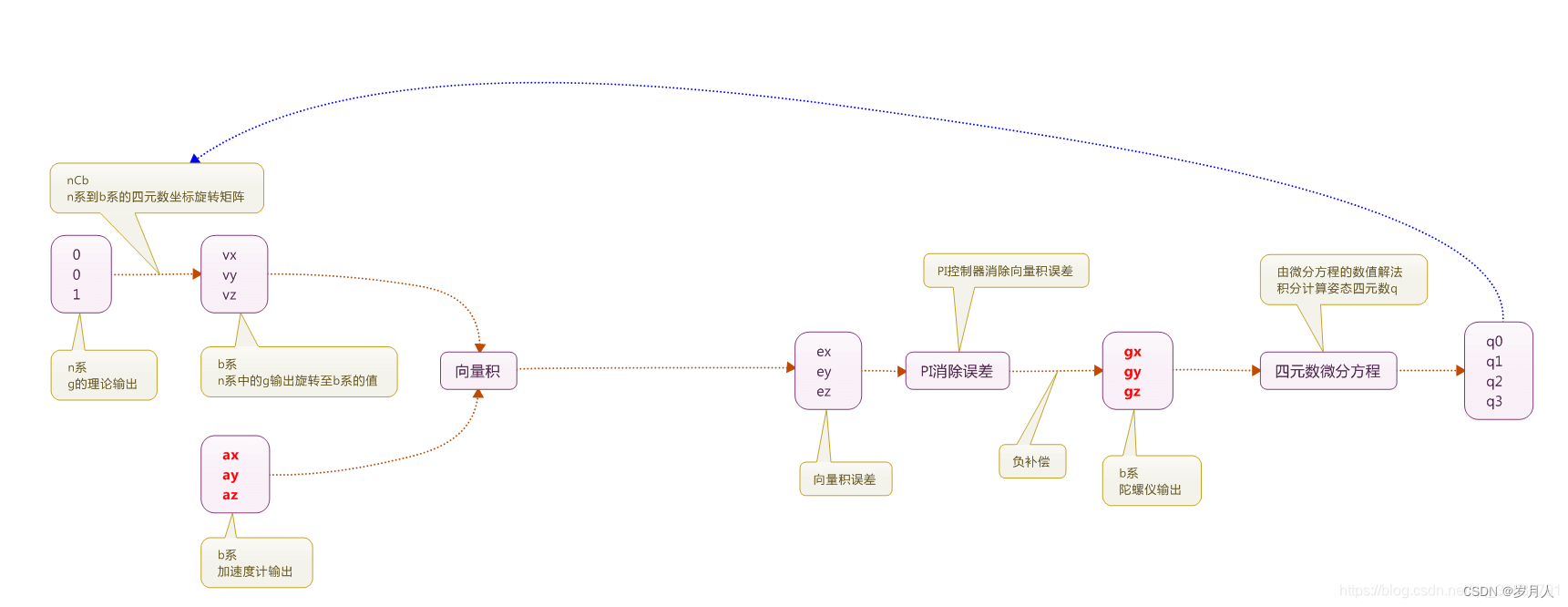
在这里插入图片描述

原理解释
n系的加速度归一化,也就是地球参考坐标系的加速度为重力加速度,按道理在x,y,z轴为0,0,g,归一化为0，0，11
通过余弦矩阵的第三行得到在机体坐标系下加速度的投影向量
通过陀螺仪测量值与重力加速度通过四元数转换到机体坐标系的加速度进行向量叉乘从而获得误差e
通过KI积分补偿误差,并通过KP与角速度数据融合
通过一阶龙格库塔法更新四元数

向量叉乘含义: 为a向量在b向量上的投影
所以可以将重力加速度在地球坐标系下的值投影到机体坐标系，从而与陀螺仪测量值进行比较

余弦矩阵第三行的含义
每一行代表x1、y1、z1分别在(x，y,z)轴上的分量,所以第三行可以表示在z轴的投影

实践篇

mahony算法实现

void imuUpdate(Axis3f acc, Axis3f gyro, state_t *state , float dt)	/*数据融合 互补滤波*/
{
	float normalise;
	float ex, ey, ez;
	float halfT = 0.5f * dt;
	float accBuf[3] = {0.f};
	Axis3f tempacc = acc;
	// 角速度
	gyro.x = gyro.x * DEG2RAD;	/* 度转弧度 */
	gyro.y = gyro.y * DEG2RAD;
	gyro.z = gyro.z * DEG2RAD;

	/* 加速度计输出有效时,利用加速度计补偿陀螺仪*/
	if((acc.x != 0.0f) || (acc.y != 0.0f) || (acc.z != 0.0f))
	{
		/*单位化加速计测量值*/
		normalise = invSqrt(acc.x * acc.x + acc.y * acc.y + acc.z * acc.z);
		acc.x *= normalise;
		acc.y *= normalise;
		acc.z *= normalise;

		// 矩阵第三行
		rMat[2][0] = 2.0f * (q1q3 + -q0q2);
	    rMat[2][1] = 2.0f * (q2q3 - -q0q1);
	    rMat[2][2] = 1.0f - 2.0f * q1q1 - 2.0f * q2q2;

		/*加速计读取的方向与重力加速计方向的差值，用向量叉乘计算*/
		ex = (acc.y * rMat[2][2] - acc.z * rMat[2][1]);
		ey = (acc.z * rMat[2][0] - acc.x * rMat[2][2]);
		ez = (acc.x * rMat[2][1] - acc.y * rMat[2][0]);
		
		/*误差累计，与积分常数相乘*/
		exInt += Ki * ex * dt ;  
		eyInt += Ki * ey * dt ;
		ezInt += Ki * ez * dt ;
		
		/*用叉积误差来做PI修正陀螺零偏，即抵消陀螺读数中的偏移量*/
		gyro.x += Kp * ex + exInt;
		gyro.y += Kp * ey + eyInt;
		gyro.z += Kp * ez + ezInt;
	}
	/* 一阶龙格库塔算法，四元数运动学方程的离散化形式和积分 */
	float q0Last = q0;
	float q1Last = q1;
	float q2Last = q2;
	float q3Last = q3;
	q0 += (-q1Last * gyro.x - q2Last * gyro.y - q3Last * gyro.z) * halfT;
	q1 += ( q0Last * gyro.x + q2Last * gyro.z - q3Last * gyro.y) * halfT;
	q2 += ( q0Last * gyro.y - q1Last * gyro.z + q3Last * gyro.x) * halfT;
	q3 += ( q0Last * gyro.z + q1Last * gyro.y - q2Last * gyro.x) * halfT;
	
	/*单位化四元数*/
	normalise = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3);
	q0 *= normalise;
	q1 *= normalise;
	q2 *= normalise;
	q3 *= normalise;
	
	imuComputeRotationMatrix();	/*计算旋转矩阵*/
	
	/* 四元数计算roll pitch yaw 欧拉角*/
	state->attitude.pitch = -asinf(rMat[2][0]) * RAD2DEG; 
	state->attitude.roll = atan2f(rMat[2][1], rMat[2][2]) * RAD2DEG;
	state->attitude.yaw = atan2f(rMat[1][0], rMat[0][0]) * RAD2DEG;

}