时间复杂度定义:在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
时间复杂度
时间复杂度是算法执行时间随输入规模增长而增长的量度,通常用大 O 记号表示。它反映了算法在解决问题时所耗费的时间资源,也可以理解为算法的运行效率。时间复杂度分析的目的是确定算法执行时间与输入规模之间的关系,并帮助我们选择更高效的算法来解决问题。
提到时间复杂度,第一时间想到的是算法,简单说,算法就是你解决问题的方法,而你用这个方法解决这个问题所执行的语句次数,称为语句频度或者时间频度,记为T(n)。
那么问题来了,我们为什么要引入这些个概念呢。因为我们想要的是执行一个算法耗费的时间,这个时间理论上可以得到,但是,要得到这个时间就必须要上机测试,但是有这个必要吗?我们需要知道的是哪一个算法需要的时间多,哪一个算法需要的时间少,这样就可以了。而且,算法的耗时和语句的执行次数是成正比的,即语句执行越多,耗时越多。这也就是我们引入概念的原因。
在上面提到的时间频度T(n)中,n是指算法的规模,n不断的变化,T(n)就会不断的变化,而这些变化的规律是怎样的呢?于是我们引入了时间复杂度的概念。
什么是时间复杂度,算法中某个函数有n次基本操作重复执行,用T(n)表示,现在有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。通俗一点讲,其实所谓的时间复杂度,就是找了一个同样曲线类型的函数f(n)来表示这个算法的在n不断变大时的趋势 。当输入量n逐渐加大时,时间复杂性的极限情形称为算法的“渐近时间复杂性”。
我们用大O表示法表示时间复杂性,它是一个算法的时间复杂性。大O表示只是说有上界但并不是上确界。
“大O记法”:在这种描述中使用的基本参数是 n,即问题实例的规模,把复杂性或运行时间表达为n的函数。这里的“O”表示量级 (order),比如说“二分检索是 O(logn)的”,也就是说它需要“通过logn量级的步骤去检索一个规模为n的数组”记法 O ( f(n) )表示当 n增大时,运行时间至多将以正比于 f(n)的速度增长。
时间复杂度对于算法进行的分析和大致的比较非常有用,但是真正的情况可能会因为一些其他因素造成差异。比如一个低附加代价的O(n2)算法在n较小的情况下可能比一个高附加代价的 O(nlogn)算法运行得更快。但是,n越来越大以后,相比较而言较慢上升函数的算法会运行的更快。
时间复杂度是渐进的
常见的时间复杂度有:O(1)、O(log n)、O(n)、O(n log n)、O(n²) 等。其中,O(1) 表示算法的执行时间不随输入规模增长而增长;O(log n) 表示算法的执行时间随输入规模增长而增长,但增长速度非常缓慢;O(n) 表示算法的执行时间与输入规模成线性增长关系;O(n log n) 表示算法的执行时间随输入规模增长而增长,并且增长速度介于线性和平方之间;O(n²) 表示算法的执行时间随输入规模增长而呈现平方级别的增长。
在实际的算法设计和分析中,我们通常关注最坏情况下的时间复杂度,即算法在处理最难的输入时所需的时间。
如果我们将算法中的一次计算记为 1,那么如果有 n 个输入值,算法对每一个输入值做一次运算,那么整个算法的运算量即为 n。这个时候,我们就可以说,这是一个时间复杂度为 O(n) 的算法。
同理,如果仍有 n个输入值,但算法对每一个输入值做一次运算这个操作需要再重复n次,那么整个算法的运算量即为n*n = n^2,时间复杂度为 O(n^2) 。
这时如果对每一个输入值做一次运算,而这个操作需要重复n+1次,算法运算量变为:
n(n+1) = n^2 + n。
这时的时间复杂度是否改变为O(n^2+n)呢?
上文曾提到时间复杂度考察的是当输入量趋于无穷时的情况,所以当 n趋于无穷的时候,n^2 对算法运行时间占主导地位,而 n 在 n^2 面前就无足轻重,不计入时间复杂度中。
换句话说,因为n^2 + n渐近地(在取极限时)与 n^2相等。此外,就运行时间来说,n 前面的常数因子远没有输入规模 n的依赖性重要,所以是可以被忽略的,也就是说O(n^2)和 是O(n^2/2)相同时间复杂度的,都为O(n^2)。
简单算法的时间复杂度举例
O(1)的算法是一些运算次数为常数的算法。例如:
temp=a;a=b;b=temp;
上面语句共三条操作,单条操作的频度为1,即使他有成千上万条操作,也只是个较大常数,这一类的时间复杂度为O(1)。
O(n)的算法是一些线性算法。例如:
sum=0;
for(i=0;i<n;i++)
sum++;
上面代码中第一行频度1,第二行频度为n,第三行频度为n,所以f(n)=n+n+1=2n+1。所以时间复杂度O(n)。这一类算法中操作次数和n正比线性增长。
O(logn) 一个算法如果能在每个步骤去掉一半数据元素,如二分检索,通常它就取 O(logn)时间。举个栗子:
int i=1;
while (i<=n)
i=i*2;
上面代码设第三行的频度是f(n), 则:2的f(n)次方<=n;f(n)<=log₂n,取最大值f(n)= log₂n,所以T(n)=O(log₂n ) 。
O(n²)(n的k次方的情况)最常见的就是平时的对数组进行排序的各种简单算法都是O(n²),例如直接插入排序的算法。
而像矩阵相乘算法运算则是O(n³)。
举个简单栗子:
sum=0;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
sum++;
第一行频度1,第二行n,第三行n²,第四行n²,T(n)=2n²+n+1 =O(n²)
O(2的n次方) 比如求具有n个元素集合的所有子集的算法
O(n!) 比如求具有N个元素的全排列的算法
时间复杂度按n越大算法越复杂来排的话:常数阶O(1)、对数阶O(logn)、线性阶O(n)、线性对数阶O(nlogn)、平方阶O(n²)、立方阶O(n³)、……k次方阶O(n的k次方)、指数阶O(2的n次方)。
借用别人的图:
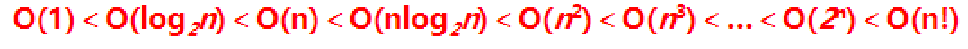
总结
时间复杂度是一个衡量算法运行效率的概念,表示随着问题规模n的增加,算法所需的执行时间的增速。一般用大O符号来表示,称为“大O记号”,如O(1)、O(log n)、O(n)、O(n log n)等。
不同的算法在处理同一问题时,其时间复杂度可以有明显的差异,因此选择高效的算法对于解决大规模数据问题时尤为重要。
时间复杂度的目的是为了帮助我们在实际开发中,选择更优秀的算法来解决具有不同规模的问题。因为对于大规模的问题,其时间复杂度的差异会直接影响到算法的实际执行效率。因此,我们需要在算法设计时考虑时间复杂度,选择最优的算法来处理实际的问题。
需要注意的是,时间复杂度并非表示具体的执行时间,而是代表了算法执行时间和输入规模之间的关系,因此只能用于算法之间的比较,不能直接用于预测算法的实际执行时间。