如何评价生成式模型的效果？

Quality: 真实性（逼真，狗咬有四条腿）

Diversity: 多样性（哈巴狗，金毛，吉娃娃，中华田园犬）

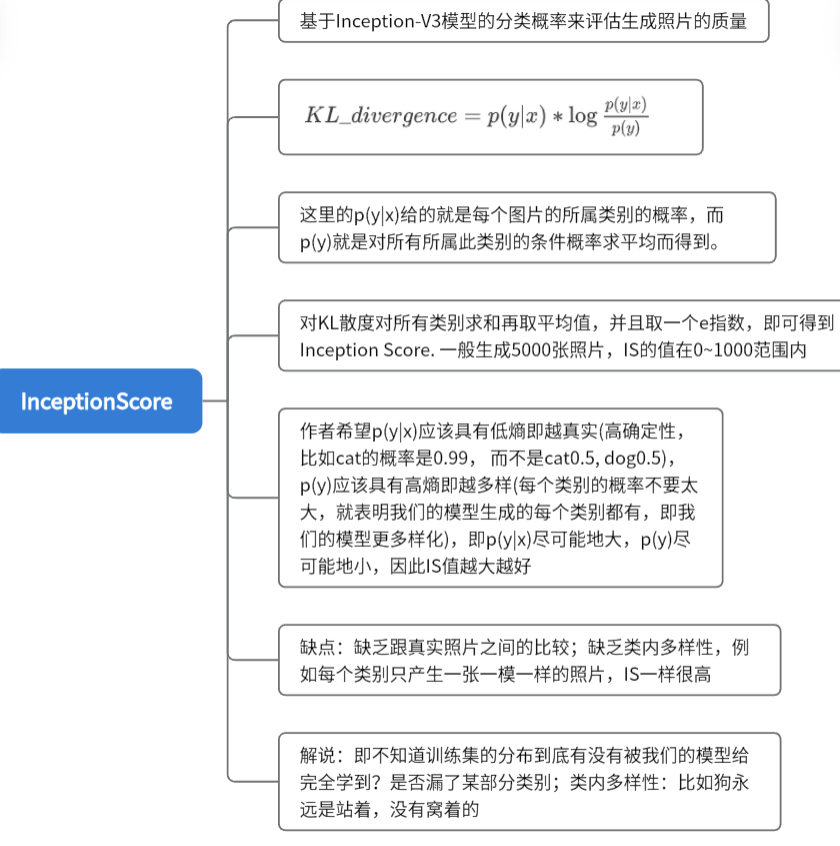
IS

Inception Score
$KL=p(y|x)\ast log\frac{p(y|x))}{log(p(y)}$

Inception-V3是一个图像分类的模型，在imageNet上进行训练得到的预训练模型

p(y|x)：即我们的模型生成的照片，它属于某个类别的概率

p(y)：即边缘概率

#用代码实现IS 
def calculate_inception_score(p_yx, eps=1E-16):
    # p_yx 即p(y|x)
    # calculate p(y)
    p_y = expand_dims(p_yx.mean(axis=0), 0)
    #kl divergence for each image
    kl_d = p_yx * (log(p_yx + eps) - log(p_y + eps))
    # sum over classes 
    sum_kl_d = kl_d.sum(axis=1)
    # average over images 
    avg_kl_d = mean(sum_kl_d)
    # undo the logs 
    is_score = exp(avg_kl_d)
    return is_score

FID

Frechlet Inception Distance(FID)

鉴于IS的缺点，就有了FID的出现，它是一个距离的量，即和真实的图片(训练集)的一个对比

FID也是用Inception-V3这个预训练好的图像分类模型，但它用的不是分类概率了，而是中间的一个feature vectors

即：把生成的照片和训练集中真实的照片同时送入到Inception-V3中，将二者经过Inception-V3模型得到的中间的特征向量拿出来，算出一个高斯分布的统计量，再去计算这两个分布之间的一个W2距离。

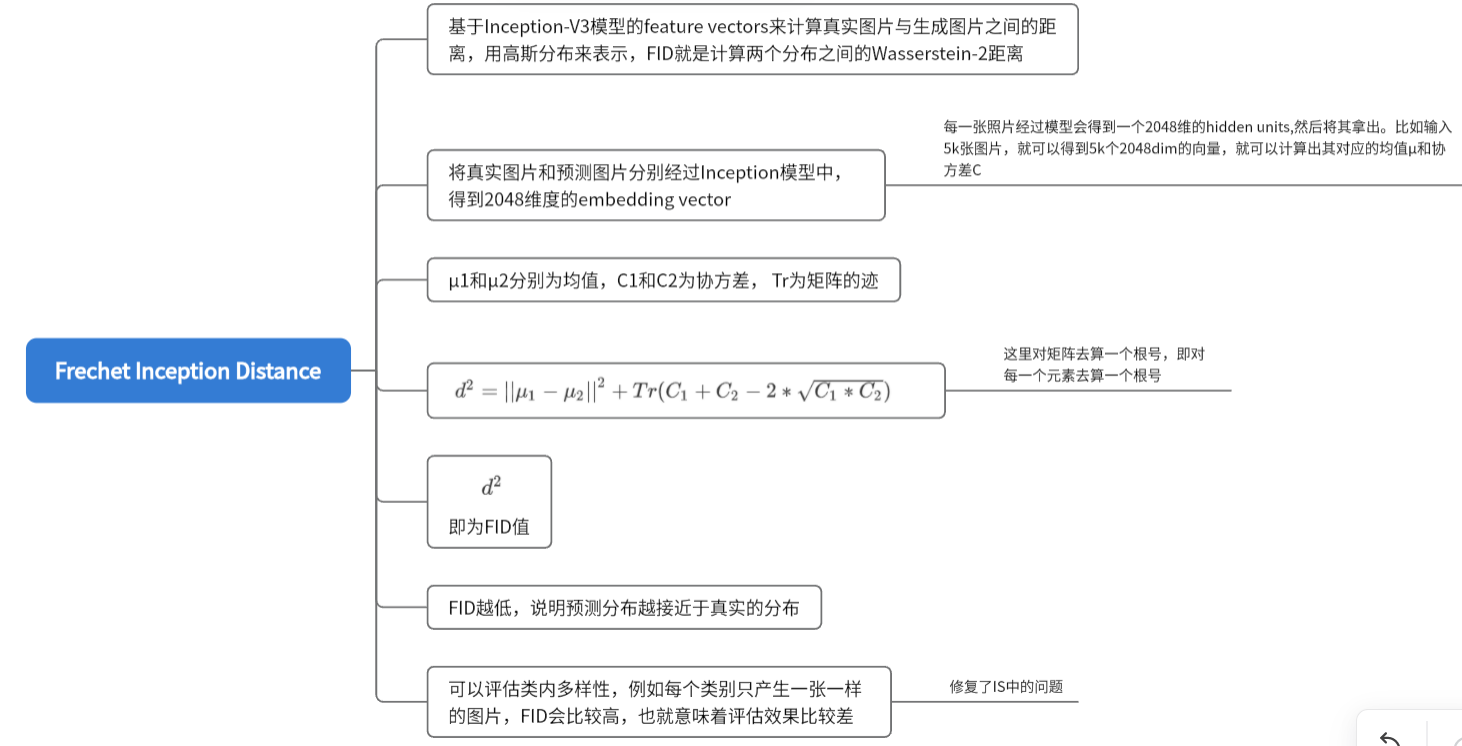
$d^2=||{\mu }_1-{\mu }_2|{|}^2+Tr(C_1+C_2-2\sqrt{C_1\ast C_2})$

# 用代码实现FID

def calculate_fid(act1, act2):
    '''
    act1:2048dim的隐变量，真实的图片送入Inception-V3中得到的
    act2:2048dim的隐变量，预测的图片送入Inception-V3中得到的
    '''
    # calculate mean and covariance statistics 
    mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False)
    mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False)
    # calculate sum squared difference between means 
    ssdiff = numpy.sum((mu1 - mu2)**2.0)
    # calculate sqrt of product between cov 
    covmean = sqrtm(sigma1.dot(sigma2))
    # check and correct imaginary numbers from sqrt 
    if iscomplexobj(covmean):
        covmean = covmean.real
    # calculate score 
    fid = ssdiff + trace(sigma1 + sigma2 - 2.0 * covmean)
    return fid

对于IS和FID，一般都是同时使用，而不是只使用其中一个

sFID

sliding Frechlet Inception Distance
和FID的不同就是用的隐变量不同，FID的隐变量是池化后的，sFID使用的是未经池化的隐变量

Precision & Recall

在生成式模型中，Precision（精确率）和Recall（召回率）通常用于评估生成的样本质量和多样性。以下是生成模型中计算Precision和Recall的常见方法：

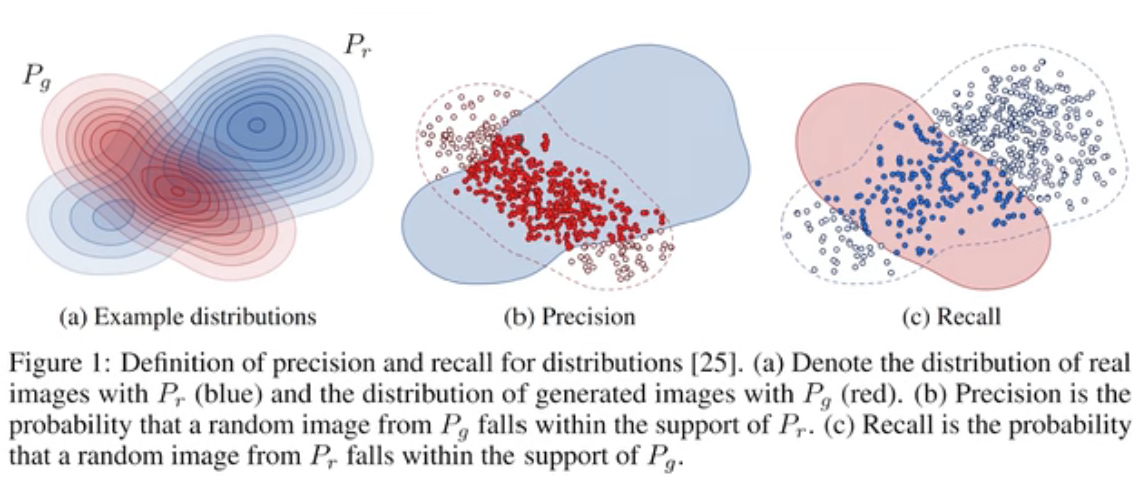
generated 分布用红色表示，real分布用蓝色表示

precision: 即红色的占蓝色分布的比例，即预测出来的样本占真实分布的比例

recall：即蓝色的点占红色的分布的比例，即真实的样本占预测分布的比例

理想情况是PR都大

Precison

Precision（精确率）：Precision衡量生成的样本中有多少是真实样本的正确生成。它是通过计算生成样本中与真实样本匹配的比例来衡量的。一种常见的方法是使用K最近邻（K-nearest neighbors）来评估生成样本与真实样本之间的相似度。具体步骤如下：

对于每个生成样本，通过计算其与真实样本之间的距离（如欧氏距离或余弦相似度），找到其K个最近邻真实样本。
计算这K个最近邻中有多少真实样本，即与生成样本匹配的数量。
最后，将匹配数量除以生成样本的总数，得到Precision。

Recall

Recall（召回率）：Recall衡量生成样本中成功覆盖真实样本的能力。它是通过计算真实样本中与生成样本匹配的比例来衡量的。具体步骤如下：

对于每个真实样本，通过计算其与生成样本之间的距离，找到其K个最近邻生成样本。
计算这K个最近邻中有多少是真实样本，即与真实样本匹配的数量。
最后，将匹配数量除以真实样本的总数，得到Recall。

计算precision和recall

用的是中间特征，而不是原图片本身

先把样本表示为$N\times D$, $D$表示特征的维度， $N$表示为样本的个数

参考样本为：$N1\times D$ , 生成样本为：$N2\times D$

用KNN的方法，求出每个样本的k近邻，具体做法为：

用manifold_radii来求出每个元素的k个近邻的距离，求出radius后，

交叉去验证real分布中属于generative的样本的个数，计算得到precision

验证generative分布中属于real的样本的个数，计算得到recall

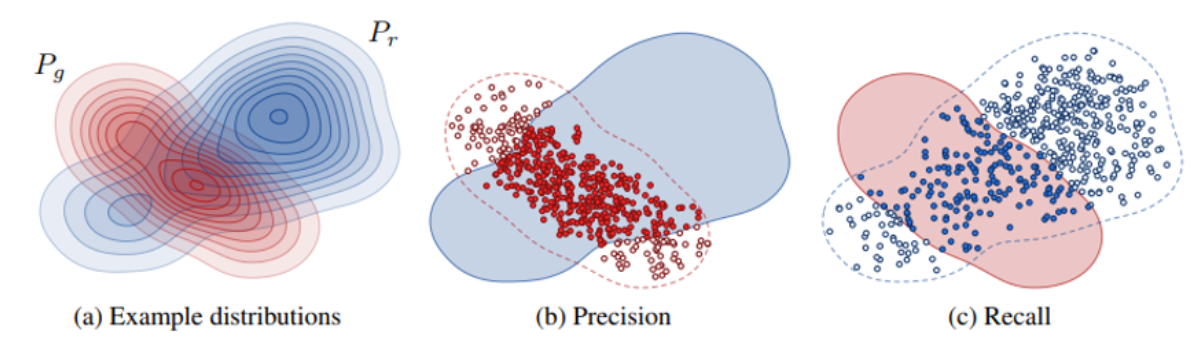
如何去获取real和generative的分布呢？

高效计算Precision和Recall。它比较两个批次的特征向量，根据流形半径判断它们是否在彼此的流形内。

将原始的N个图片 --> 表示为矩阵 $N\times D$

求得每个样本的 k 个近邻，即求得一个范围，相当于以每个样本为中心，画个圈，这样就可以表示出 real 的分布了，同理于generative分布,如下图所示。

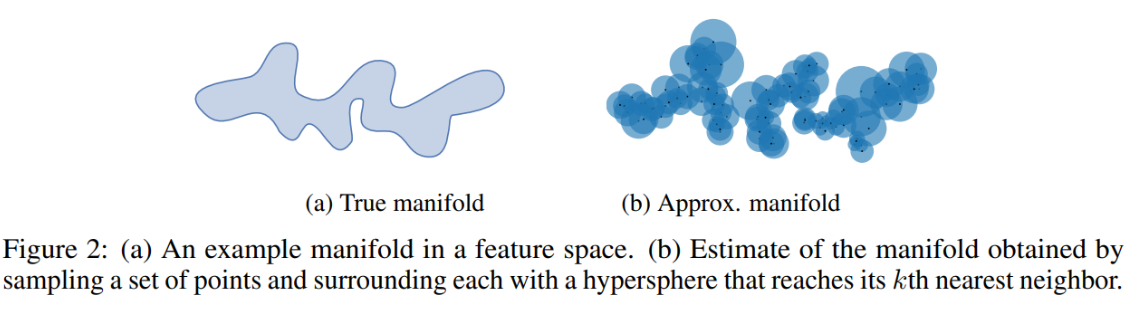
• Precision: 以real的每个样本为中心，画圈，计算real中的每个样本和generative中的每个样本的距离，如果在圈内，则说明是(b)中的红色实心部分， 红色实心部分占比与整个蓝色的部分
• Recall：以generative的每个样本为中心，画圈，计算generative中的每个样本和real中的每个样本的距离，如果在圈内，则说明是©中的蓝色实心部分，蓝色实心部分占比与整个红色部分