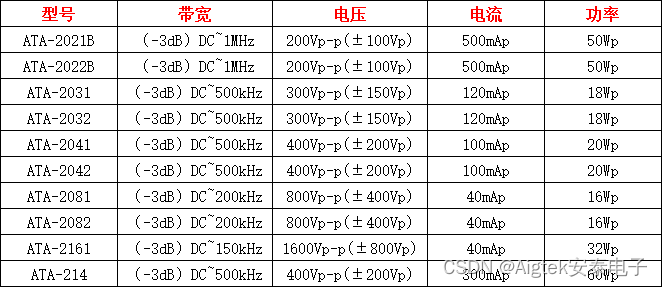
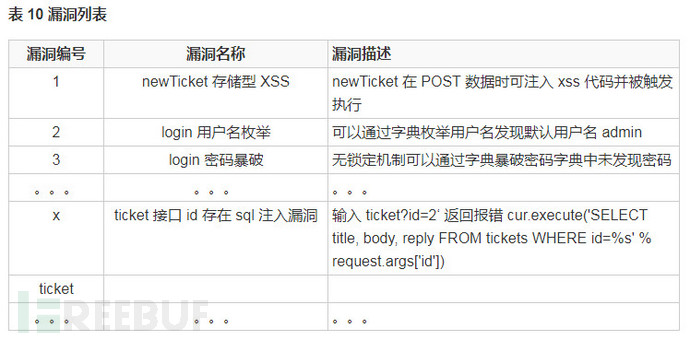
1.01背包问题

问题介绍：有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

1.二维数组实现思想

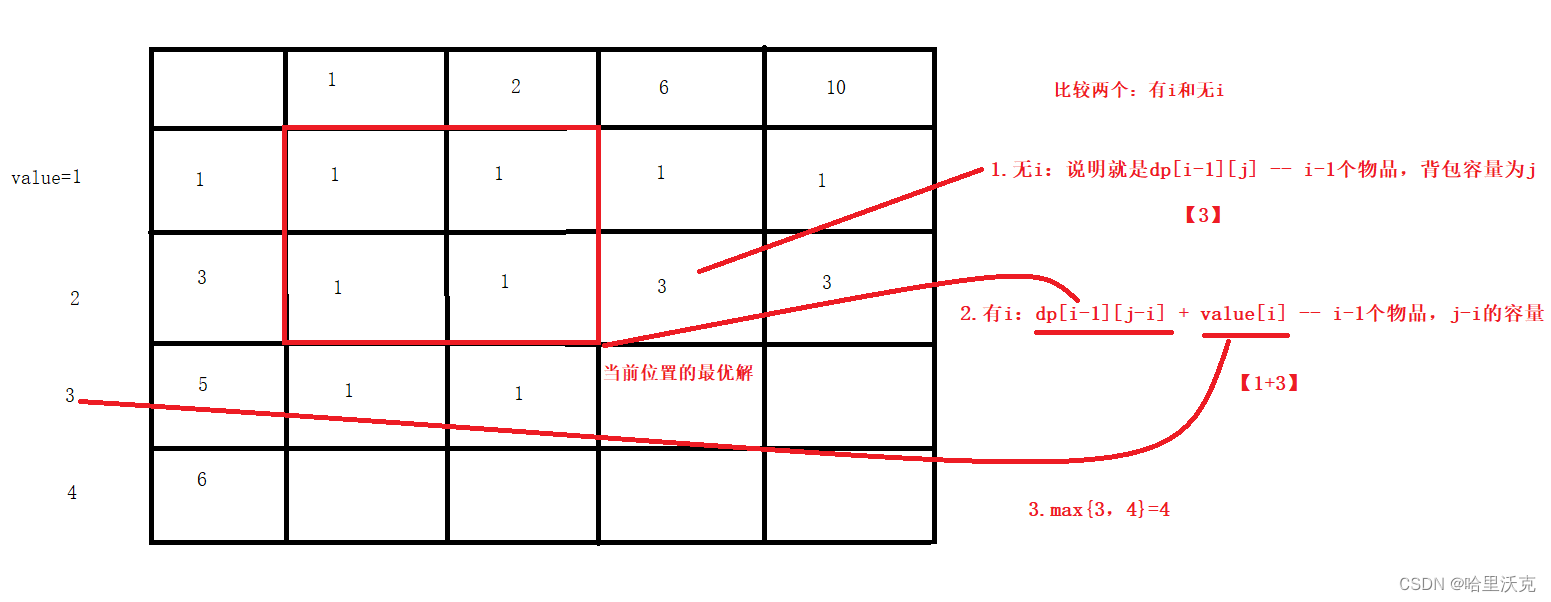
1.dp[i][j]的含义：首先i为物品的序号；j为背包的大小；dp[i][j]为当前[0~i]的物品中，背包容量为j时，所能得到的最大价值。其实就是只有i个物品，j大小背包，所能装的局部最优解。那么也就是说dp数组的右下角就是最终最优解

2.局部最优解的得出，dp数组的条件由来：核心思路就是一句话当一个物品摆在我们面前，我们只有选择或者不选择，那么我们选择塞入背包就意味着不管是否要将其他东西被替换掉，我们最后背包的价值能否比之前的背包价值要多。那就是两个情况，当面对第i个物品时，我们有选择塞入或者不选择塞入的情况：不选择塞进去的最优解就是前i-1个物品，j大小背包对应的局部最优解dp[i-1][j]；选择塞进去，那么能确定的是i一定在里面，那么自然当前的背包容量变小了，那么我们要得到的就是当背包变为减去i对应重量是对应的局部最优解，即value[i]（i对应的价值）+dp[i-1][j-weight[i]]（j背包容量减去i重量对应的最优解）。

3.初始化：首先我定义的二维数组有0物品的行和0背包容量的列，所以将这列和行都定义为0；此外我们能发现，其实除了对应的dp[0][j]和dp[i][0]需要被初始化，其他的结果都是由这两行不断计算其他的推出来的

//bagweight:背包大小
//weight：不同物品对应的大小
//value：不同物品对应的价值
int bag_problem(int& bagweight, vector<int>& weight, vector<int>& value)
{
	vector<vector<int>> dp(weight.size()+1, vector<int>(bagweight + 1, 0));
	for(int i = 1; i <= bagweight; i++)
	{
		for (int j = 1; j <= weight.size()-1; j++)
		{
			dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
		}
	}
	return dp[bagweight][weight.size() - 1];
}

2.一维数组实现思想

1.dp[j]的含义：背包容量为j时的最大价值

2.dp数组条件：i为遍历的物品。如果i不放进去，那dp[j]=dp[j]，需要注意的是右边的dp[j]是上一轮循环的结果，表示上一次的最大值仍然适用；如果i放进去，dp[j]=dp[j-weight[i]]+value[i]。那么我们其实就是在这两者之间取较大值作为结果，那么其条件就是dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

3.循环的问题：我们先遍历物品再遍历背包，这样的含义其实就是再不断加入物件的过程之中不断更新当前每一个容量下背包的最优解。不过背包的遍历顺序我们希望它是倒叙的，为什么？因为我们想要得到当前的大背包的最优解一定会去判断小背包，那么都是在同一层的情况下，从大到小遍历意味着当前大背包的量比较的就是上一次的最优解（如2所说“右边的dp[j]是上一轮循环的结果”），如果从小到大，那小的背包更新为当前的循环，那么意味着大背包的比较值是建立在当前的小背包最优解，不符合我们想要的条件比较。

4.初始化：全部初始化为0

//bagweight:背包大小
//weight：不同物品对应的大小
//value：不同物品对应的价值
int bag_problem(int& bagweight, vector<int>& weight, vector<int>& value)
{
	vector<int> dp(bagweight + 1, 0);
	for (int i = 1; i <= weight.size() - 1; i++)
	{
		for (int j = bagweight; j >= weight[i]; j--)
		{
			dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
		}
	}
	return dp[bagweight];
}

2. 分割等和子集

416. 分割等和子集

其实就是01背包的应用。求sum/2的背包，装下的最大数是否相同，如果相同则返回true。

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int target = 0;
        for(auto e: nums)
            target+=e;
        if(target%2==1)
            return false;
        target/=2;
        vector<int>dp(20001,0);
        for(int i=0;i<nums.size();i++)
        {
            for(int j=target;j>=nums[i];j--)
                dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);
        }
        if(dp[target]==target)
            return true;
        return false;
    }
};