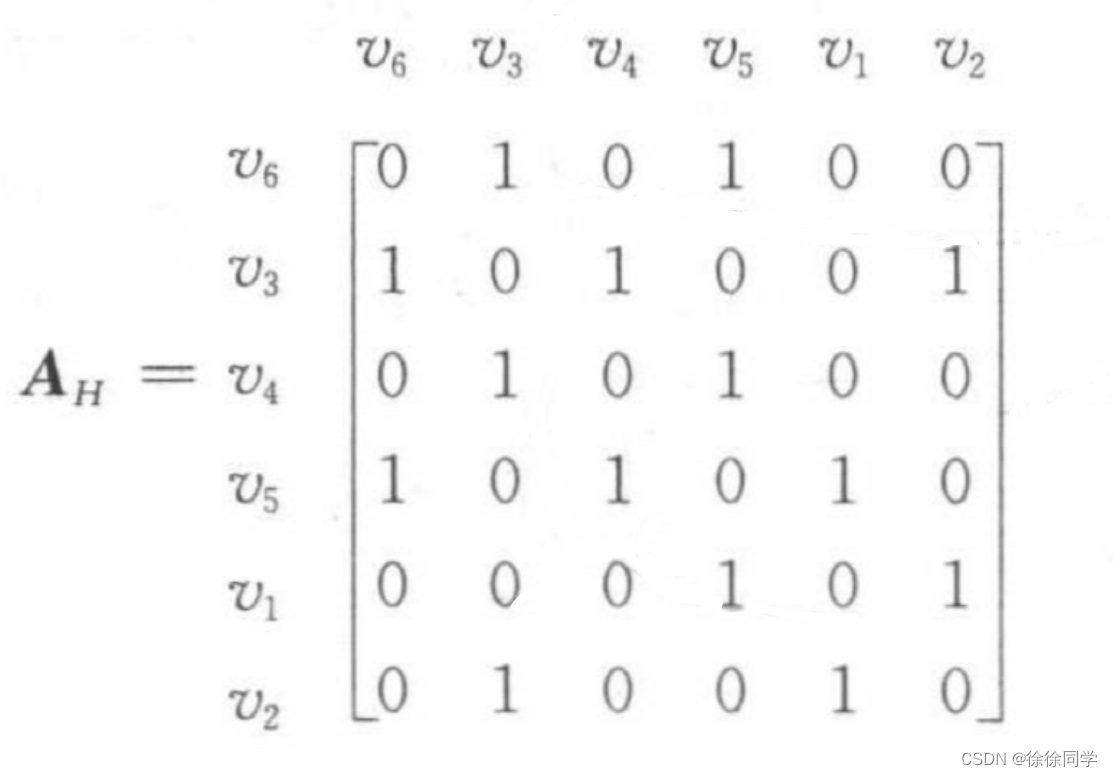
1.分治法
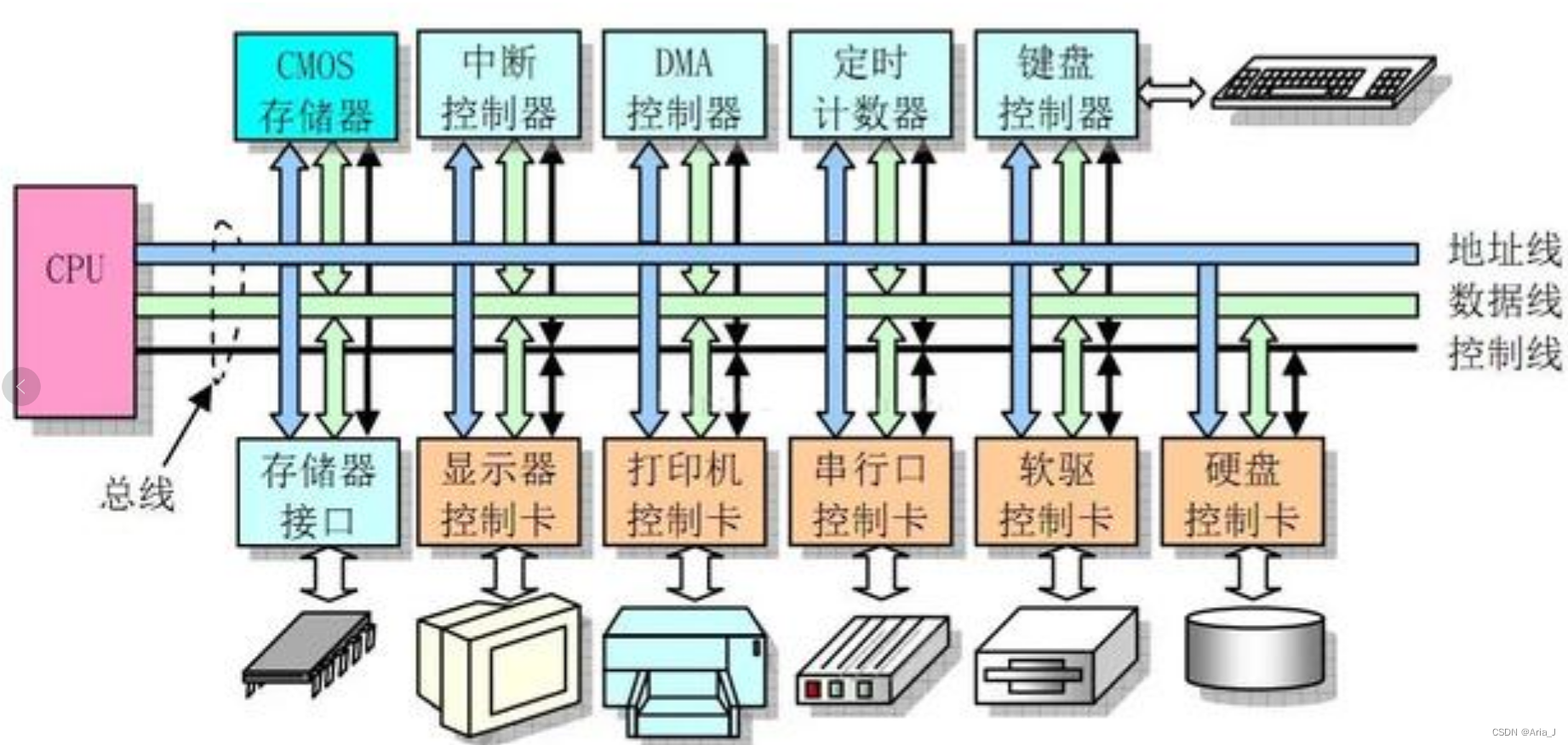
分治法也叫做分而治之法。核心思想是将一个难以直接解决的大问题依照相同的概念分割成两个或者多个相同的小问题,以便各个击破。
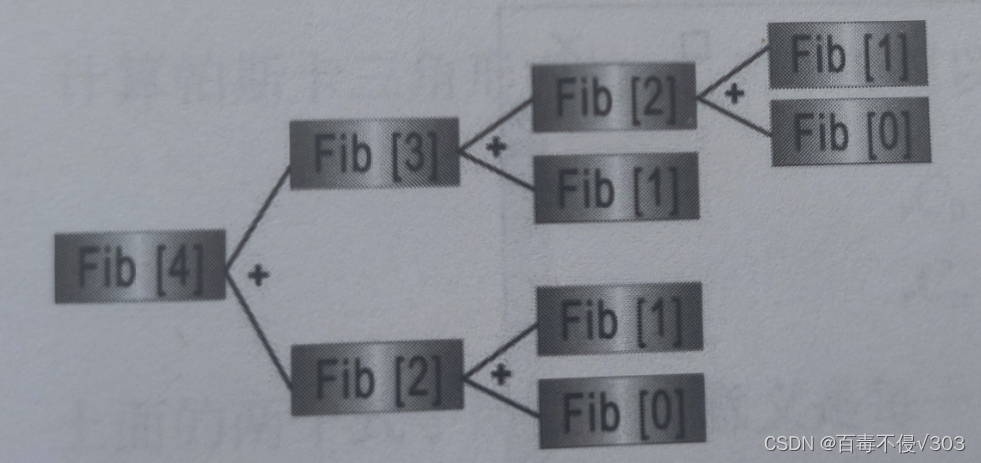
如图所示:
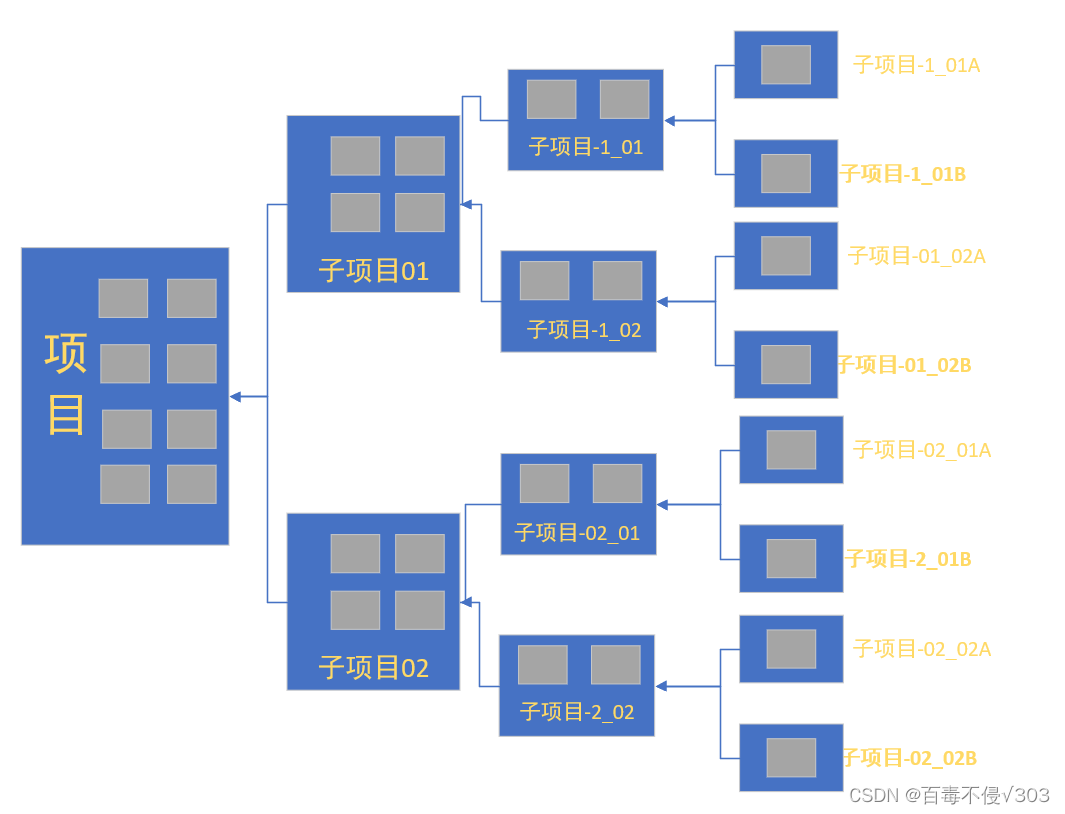
2.递归法
递归法和分而治之法像一对孪生兄弟,都是将一个复杂的算法问题进行分解,使其规模变小,然后使子问题容易求解。
一个函数或子程序是由自身所定义或调用的,就称为递归。它有两种定义,包括一个可以反复执行的递归过程和一个跳出只从过程的出口。
注:尾递归是指函数或子程序的最后一句为递归调用,,因为每次调用后再回到前一次掉哦哦用的第一条语句,所以不需要再 进行任何运算。
再系统种具体实现递归时要用到堆栈的数据结构。所谓堆栈,就是一组相同数据类型的集合,所有的操作均在结构的顶端进行,具有“后进先出”的特征。
3.贪心法
贪心法又称为贪婪算法,从某一七点开始,在每一个解决问题的步骤中使用贪心算法,即采用再当前状态下最有利或者最优化的选择,持续在每一个步骤中选择最佳方法,并且逐步逼近给定的目标,当达到某一个步骤不能再继续前进时,算法停止。
哈夫曼编码经常应用于数据的压缩,是可以根据数据的出现频率来构建二叉树。数据的存储时数据处理的两个重要领域,两者都和数据量的大小息息相关,哈夫曼树正好可以解决数据大小的问题。
4.动态规划法
类似于分治法。
如果一个问题的答案与子问题相关,就能将大问题拆解成小问题没其中与分治法最大的不同就是可以将每一个子问题的答案都存储起来,这样的做法不但可以减少再次计算的时间,而且可以将这些解组合成大的问题的解,故而可以解决再次计算的问题。
5.迭代算法
我无法使用公式一次求解,而需要使用重复结构重复执行一段程序代码来求得答案。
6.枚举法
枚举法是一种常见的数学方法,核心思想是列举所有的可能。
根据问题要求逐一列举问题的答案,或者为了便于解决问题把问题分为不重复、不遗漏的有限种可能情况,并 加以解决,最终达到解决问题的目的。
7.回溯法
回溯法也是枚举法的一种。对于某些问题而言,回溯法是一种可以找出所有解的一般性算法,同时避免美剧不正确的数值。一旦发现不正确的数值,回溯法就不再低轨道下一层,而是回溯到刷上一层你,以节省时间,是一种走不通就退回再走的方式。它的特点主要时搜索过程种寻找问题的解,当发现不满足求解条件时就回溯,尝试别的路径,避免无效搜索。
今天就到这里了,今天主要记录了几种常用算法,并且有大致的解释,接下来将会一一解释各个算法的作用及用法。