本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
六、 线搜索求步长
1、0.618方法
0.618方法方法适合于 单峰函数 ,既具有“高-低-高”形状的函数,然而,在众多问题中,我们所面对的函数不可能都是单峰函数,所以实际上我们也用这种方法处理一般一维函数的极小问题。
在使用0.618方法求解近似满足于精确线搜索准则的步长之前,可以使用“进退法”得到初始搜索区间。
用“进退法”求初始区间[a,b],要求在该区间中,目标函数ψ(a)呈“高―低―高”的形状。该方法的基本思想是:先选定初始点
α
0
α_0
α0 > 0 和一个初始步长
γ
0
γ_0
γ0 > 0,从
α
0
α_0
α0 起以
γ
0
γ_0
γ0为步长向前搜索一步,得
α
0
α_0
α0+
γ
0
γ_0
γ0.若这一点的目标函数值较
α
0
α_0
α0处的目标函数值减小了(说明极值点在选取的初始点右侧,继续向右搜索),则加大
γ
0
γ_0
γ0,继续向前搜索,直至新一点的目标函数值较前一点的目标函数值增大了,搜索结束。
若最初从
α
0
α_0
α0起以
γ
0
γ_0
γ0 初始步长进行第一次搜索的时候,新到达的点处的函数值大于
α
0
α_0
α0 点处的函数值,说明极值点在选取的初始点左侧,则应该向相反方向搜索,即将步长取负,其余过程同上.
无论是向前搜索还是向后搜索.最后可得a≤c≤b,使下式成立
φ ( c ) ⩽ φ ( b ) , φ ( c ) ⩽ φ ( a ) . \varphi(c)\leqslant\varphi(b),\quad\varphi(c)\leqslant\varphi(a). φ(c)⩽φ(b),φ(c)⩽φ(a).
进退法的具体迭代步骤如下:

使用“进退法”得到初始搜索区间后,接下来就是使用0.618方法求解近似满足于精确线搜索准则的步长了
0.618方法的基本思想是:将初始区间[a,b]按0.618的比例不断缩小,使ψ(a)的极小点α*始终包含在缩小后的区间中;重复这个过程,直至区间长度足够小,区间中的点均接近极小点为止.
接下来讨论其具体做法及为何要按照0.618的比例缩小,设ψ(a)是区间[a0,b0]上的单峰函数,我们在[a0,b0]上取两个点 α 0 l , α 0 r , \alpha_0^l,\alpha_0^r, α0l,α0r,为使得缩小后的区间是对称的,两个点满足下式:
α 0 r − a 0 = b 0 − α 0 l = τ ( b 0 − a 0 ) , τ > 1 2 , \alpha_0^r-a_0=b_0-\alpha_0^l=\tau(b_0-a_0),\quad\tau>\dfrac{1}{2}, α0r−a0=b0−α0l=τ(b0−a0),τ>21,
即:
α 0 i = a 0 + ( 1 − τ ) ( b 0 − a 0 ) , α 0 r = a 0 + τ ( b 0 − a 0 ) . \begin{array}{l}\alpha_0^i=a_0+(1-\tau)(b_0-a_0),\\ \alpha_0^r=a_0+\tau(b_0-a_0).\end{array} α0i=a0+(1−τ)(b0−a0),α0r=a0+τ(b0−a0).
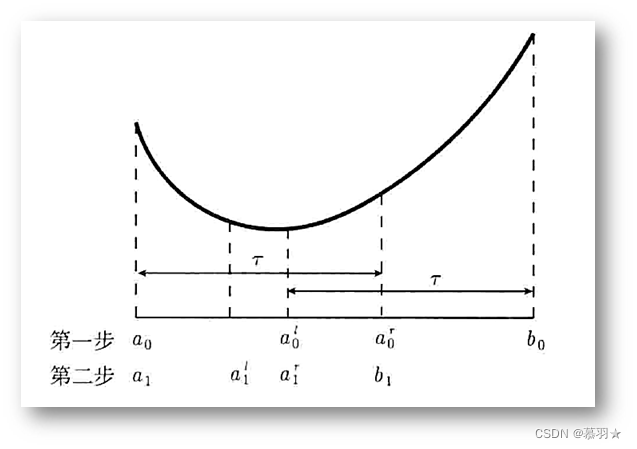
对称选取的两点 α 0 l , α 0 r , \alpha_0^l,\alpha_0^r, α0l,α0r,将区间[a0,b0]划分为有重叠的两个区间[a0, α 0 r \alpha_0^r α0r] 和[ α 0 l \alpha_0^l α0l,b0],它们的区间长度都是[a0,b0]的τ倍,若 φ ( α 0 l ) < φ ( α 0 r ) \varphi(\alpha_{0}^{l})<\varphi(\alpha_{0}^{r}) φ(α0l)<φ(α0r),则a * ∈[a0, α 0 r \alpha_0^r α0r] ,取[a1,b1]=[a0, α 0 r \alpha_0^r α0r] ,否则,a * ∈[ α 0 l \alpha_0^l α0l,b0],取[a1,b1]=[ α 0 l \alpha_0^l α0l,b0]。
在第二步迭代中,我们用上述方法以相同的比例缩小区间[a1,b1]。按上图中的例子,第一步迭代后我们选取的区间[a1,b1]=[a0, α 0 r \alpha_0^r α0r],第一步中我们已经计算出了 φ ( α 0 l ) \varphi(\alpha_{0}^{l}) φ(α0l),所以我们将已知点 α 0 l \alpha_0^l α0l作为区间[a1,b1]中要选取的两个点中的其中一点,且根据对称原则,即可计算出另一点。因此,下式成立
α 1 τ − a 1 = τ ( b 1 − a 1 ) . \alpha_1^{\tau}-a_1=\tau(b_1-a_1). α1τ−a1=τ(b1−a1).
设区间[a0,b0]的长度为L,则b1-a1=τL, α 1 τ − a 1 \alpha_1^{\tau}-a_1 α1τ−a1=(1-τ)L,代入上式,两边消去L后,有 1 − τ = τ 2 1-\tau=\tau^2 1−τ=τ2,解得 τ = 5 − 1 2 ≈ 0.61803 {\tau}=\dfrac{\sqrt{5}-1}{2}\approx0.61803 τ=25−1≈0.61803
所以,取区间的缩小比为0.618,该方法也被叫做0.618方法,其算法流程如下:

从区间[a0,b0]开始迭代,经过m次迭代后,区间长度为 τ m ( b 0 − a 0 ) τ^m(b0-a0) τm(b0−a0)
到这里0.618方法求步长的原理就介绍完了,接下来放一下我用matlab写的程序,我把进退法求初始区间的算法封装成了函数Advance_retreat_search,把0.618方法求步长的算法封装成了函数Golden_section_minima,然后在脚本文件Golden_section_minima_test中调用,这三个文件的程序如下所示:
(1) Advance_retreat_search
function [ra, rb,i] = Advance_retreat_search(f,a0,dx,k,max_i)
%% 进退法求初始搜索区间
% f:函数句柄
% a0:初始点
% dx:步长
% k:步长扩大系数,k>1
% max_i: 设定的最大迭代次数
% ra: 得到的初始区间左端点
% rb: 得到的初始区间右端点
% i: 迭代次数
%% 初始化
i=1;
alpha=0.00001; %存放其中一个端点,初始化为一较小值
a(1)=a0;
%%
while i<=max_i
a(i+1)=a(i)+dx;
%防止a[i+1]越界
if a(i+1)<=0
a(i+1)=0;
ra=a(i+1);
rb=alpha;
break
end
if f(a(i+1))>=f(a(i))
if i==1 %初始值在函数最小值的左侧,改变方向
dx=-dx;
alpha=a(i+1);
else
ra=min(alpha,a(i+1));
rb=max(alpha,a(i+1));
break
end
end
dx=k*dx;
alpha=a(i);
a(i)=a(i+1);
i=i+1;
end
end
(2)Golden_section_minima
function [optimal_a,i] = Golden_section_minima(f,ra,rb,dr)
%% 0.618法求一维函数的近似极小值
% f: 函数句柄
% ra:区间左端点
% rb:区间右端点
% dr:设定近似区间长度,可以理解为求解精度
% optimal_a:近似解
% i:迭代次数
%% 初始化
i=1;
a(1)=ra;
b(1)=rb;
Tau=0.618;
%%
while ((b(i)-a(i))>=dr)
al(i)=a(i)+(1-Tau)*(b(i)-a(i));
ar(i)=a(i)+Tau*(b(i)-a(i));
if f(al(i))<f(ar(i))
a(i+1)=a(i);
b(i+1)=ar(i);
else
a(i+1)=al(i);
b(i+1)=b(i);
end
i=i+1;
end
optimal_a=(b(i)+a(i))/2.0;
end
(3)Golden_section_minima
%% 定义函数句柄
f = @(x) 2*x^2 - 0.1*sin(x);
%f = @(x) (x+78.52)^2 ;
%% 初始化进退法求初始搜索区间的参数
x0 = 52.752; %设定初始点
dx = 0.1; %设定步长
k = 2; %设定步长扩大系数,k>1
max_i=100000; %设定的最大迭代次数
%% 初始化0.618方法求函数近似极小点的参数
dr=0.0001; %设定近似区间长度,可以理解为求解精度
%%
%调用函数求初始搜索区间
[a, b,i1] = Advance_retreat_search(f,x0,dx,k,max_i);
%调用函数求近似极小值点
[optimal_a,i2] = Golden_section_minima(f,a,b,dr);
%% 显示相关信息
fprintf('初始搜索区间: [%f, %f], 迭代次数: %d \n', a, b,i1);
fprintf('近似极小点: %f, 迭代次数: %d \n', optimal_a, i2);
2、多项式插值法
多项式插值法可以用于求近似满足精确线搜索准则或满足非精确线搜索准则的步长.这里以满足非精确线搜索准则中的Goldstein准则为例,讨论如何用插值方法求满足非精确线搜索准则的步长 a k a_k ak
基本思想:多项式函数的极小点是容易求得的,所以我们可用已有的函数信息,构造近似ψ(a)的多项式函数,求出该多项式函数的极小点并检验它是否满足非精确线搜索准则.若不满足,则根据新的函数信息去构造新的多项式函数.如此反复,一般能够求得满足非精确线搜索准则的步长.
若已知ψ(a)在m+1个不同点a0, a1, … ,am , (ai > 0,i= 0.…,m)处的函数值为ψ(ai),i=0,·… ,m,我们欲求ψ(a)在[0, 正无穷)上的近似多项式p(a),使其满足下式。
p
(
α
i
)
=
φ
(
α
i
)
,
i
=
0
,
⋯
,
m
,
p(\alpha_i)=\varphi(\alpha_i),\quad i=0,\cdots,m,
p(αi)=φ(αi),i=0,⋯,m,
满足上述条件的插值方法的几何意义就是找一条通过平面上m+1个点 { ( α i , φ ( α i ) ) } i = 0 m \{(\alpha_i,\varphi(\alpha_i))\}_{i=0}^m {(αi,φ(αi))}i=0m的代数曲线.当m +1个插值节点互不相同时,满足上述条件的次数不超过m的多项式p(a)存在唯一
根据不同的插值条件,例如上述插值条件,或利用导数信息的插值条件,我们可以得到不同的插值多项式.下面要讨论的两个插值方法,均利用了插值点的函数及其一阶导数的插值信息。
(1)两点二次插值法求步长
设在0, a 0 a_0 a0 ( a 0 a_0 a0>0)两点的函数值已知,且在0点的一阶导数已知,如下所示:
φ ( 0 ) = f ( x k ) , φ ′ ( 0 ) = ∇ f ( x k ) T d k , φ ( α 0 ) = f ( x k + α 0 d k ) . \varphi(0)=f(x_k),\quad\varphi'(0)=\nabla f\left(x_{k}\right)^\mathrm{T}d_k,\quad\varphi(\alpha_0)=f(x_k+\alpha_0d_k). φ(0)=f(xk),φ′(0)=∇f(xk)Tdk,φ(α0)=f(xk+α0dk).
假定在点a0处不满足Goldstein准则,构造如下二次插值多项式
p ( α ) = a α 2 + b α + c , p(\alpha)=a\alpha^2+b\alpha+c, p(α)=aα2+bα+c,
根据插值条件可知:
p ( 0 ) = φ ( 0 ) , p ′ ( 0 ) = φ ′ ( 0 ) , p ( α 0 ) = φ ( α 0 ) , p(0)=\varphi(0),\quad p'(0)=\varphi'(0),\quad p(\alpha_0)=\varphi(\alpha_0), p(0)=φ(0),p′(0)=φ′(0),p(α0)=φ(α0),
解得:
p ( α ) = φ ( α 0 ) − φ ( 0 ) − φ ′ ( 0 ) α 0 α 0 2 α 2 + φ ′ ( 0 ) α + φ ( 0 ) . p(\alpha)=\dfrac{\varphi(\alpha_0)-\varphi(0)-\varphi'(0)\alpha_0}{\alpha_0^2}\alpha^2+\varphi'(0)\alpha+\varphi(0). p(α)=α02φ(α0)−φ(0)−φ′(0)α0α2+φ′(0)α+φ(0).
容易知道一元二次函数的稳定点位于-b/2a处,即可得p(a)的稳定点a1为:
α 1 = − φ ′ ( 0 ) α 0 2 2 [ φ ( α 0 ) − φ ( 0 ) − φ ′ ( 0 ) α 0 ] . \alpha_1=\dfrac{-\varphi'(0)\alpha_0^2}{2[\varphi(\alpha_0)-\varphi(0)-\varphi'(0)\alpha_0]}. α1=2[φ(α0)−φ(0)−φ′(0)α0]−φ′(0)α02.
我们已经假设在a0处不满足Goldstein准则,则有
φ ( α 0 ) > φ ( 0 ) + ρ φ ′ ( 0 ) α 0 > φ ( 0 ) + φ ′ ( 0 ) α 0 , \varphi(\alpha_0)>\varphi(0)+\rho\varphi'(0)\alpha_0>\varphi(0)+\varphi'(0)\alpha_0, φ(α0)>φ(0)+ρφ′(0)α0>φ(0)+φ′(0)α0,
从而得到
p ′ ′ ( α 1 ) = 2 α 0 2 [ φ ( α 0 ) − φ ( 0 ) − φ ′ ( 0 ) α 0 ] > 0 , p''(\alpha_1)=\dfrac{2}{\alpha_0^2}[\varphi(\alpha_0)-\varphi(0)-\varphi'(0)\alpha_0]>0, p′′(α1)=α022[φ(α0)−φ(0)−φ′(0)α0]>0,
即a1点必然是p(a)的极小点,该方法因为有两个插值点,构造的是二次多项式而被称为两点二次插值法。在这个方法中,我们只考虑了Goldstein准则的第一个条件,因为在线搜索过程中我们可以为α设置一个下界,以此控制步长不要取得太小,使其满足第二个条件。
求满足Goldstein准则的步长的过程是一个子迭代的过程.上面我们由不满足该准则的a0点,求取了a1点,若在点a1,还不满足,则可以根据实际情况,利用新的信息(比如用a0点和a1点,或者0点和a1点等)继续构造新的插值多项式,一般来说,几步迭代后,即可求得满足Goldstein准则的步长,否则的话,说明p(a)不能很好地近似ψ(α),应该采用三次插值方法求步长。
下图给出了当函数ψ(a) = - sin a 时,在0,3π两点进行二次插值和在0,3π/2,3π三点进行三次插值近似的例子,图中的实直线即为Goldstein准则的第一个条件,显然,在二次插值函数的极小点处不满足该条件,而在三次插值函数的极小点处满足。
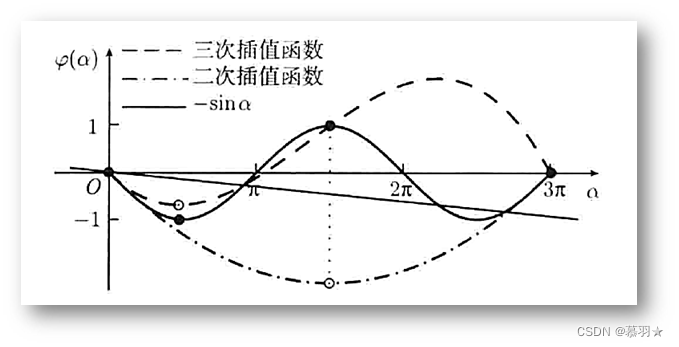
(2)三点三次插值法求步长
有了上面两点二次插值法求步长的基础,再来看三点三次插值求步长就容易很多,三点三次求步长需要先求一次二点二次插值,然后便可在0,a0>0,a1>0三点知道四个插值数据: φ ( 0 ) , φ ′ ( 0 ) , φ ( α 0 ) , φ ( α 1 ) , \varphi(0),\varphi'(0),\varphi(\alpha_0),\varphi(\alpha_1), φ(0),φ′(0),φ(α0),φ(α1),,对其可以进行三次插值,设三次插值函数为:
p ( α ) = a α 3 + b α 2 + c α + d . p(\alpha)=a\alpha^3+b\alpha^2+c\alpha+d. p(α)=aα3+bα2+cα+d.
由插值条件可得d = ψ(0), c =
ψ
′
(
0
)
ψ'(0)
ψ′(0)及下式
·
a α 0 3 + b α 0 2 + φ ′ ( 0 ) α 0 + φ ( 0 ) = φ ( α 0 ) , a α 1 3 + b α 1 2 + φ ′ ( 0 ) α 1 + φ ( 0 ) = φ ( α 1 ) . \begin{array}{c}a\alpha_0^3+b\alpha_0^2+\varphi'(0)\alpha_0+\varphi(0)=\varphi(\alpha_0),\\ a\alpha_1^3+b\alpha_1^2+\varphi'(0)\alpha_1+\varphi(0)=\varphi(\alpha_1).\end{array} aα03+bα02+φ′(0)α0+φ(0)=φ(α0),aα13+bα12+φ′(0)α1+φ(0)=φ(α1).
解这个关于a,b 的线性方程组,得
[ a b ] = 1 α 0 2 α 1 2 ( α 1 − α 0 ) [ α 0 2 − α 1 2 − α 0 3 α 1 3 ] [ φ ( α 1 ) − φ ( 0 ) − φ ′ ( 0 ) α 1 φ ( α 0 ) − φ ( 0 ) − φ ′ ( 0 ) α 0 ] . \left[\begin{array}{c}a\\ b\end{array}\right]=\dfrac{1}{\alpha_0^2\alpha_1^2(\alpha_1-\alpha_0)}\left[\begin{array}{c c}\alpha_0^2&-\alpha_1^2\\ -\alpha_0^3&\alpha_1^3\end{array}\right]\left[\begin{array}{c c}\varphi(\alpha_1)-\varphi(0)-\varphi'(0)\alpha_1\\ \varphi(\alpha_0)-\varphi(0)-\varphi'(0)\alpha_0\end{array}\right]. [ab]=α02α12(α1−α0)1[α02−α03−α12α13][φ(α1)−φ(0)−φ′(0)α1φ(α0)−φ(0)−φ′(0)α0].
由 p ′ ( a ) = 0 p'(a)=0 p′(a)=0,可求得p(a)的极小点a2 .下一步迭代的插值数据可选为 φ ( 0 ) , φ ′ ( 0 ) , φ ( α 1 ) , φ ( α 2 ) , \varphi(0),\varphi'(0),\varphi(\alpha_1),\varphi(\alpha_2), φ(0),φ′(0),φ(α1),φ(α2),亦可从0,a0,a1,a2中选ψ(a)具有“高―低-高”特性的三点。
总的来说,多项式插值法可以用于求解优化问题中的线搜索步长,但是它并不是最优或最常用的方法。以下是对该方法的评价:
优点:
① 多项式插值法是一种简单易懂的数值计算方法,容易实现和应用。
② 在某些情况下,多项式插值法可以比其它的数值计算方法更加精确地计算出线搜索步长。
③ 多项式插值法可以通过插值多项式来拟合目标函数的形状,从而帮助确定线搜索步长。
④ 多项式插值法可以不需要目标函数的一阶或二阶导数,因此可以适用于一些非光滑的函数。
缺点:
①多项式插值法可能会引入数值误差,特别是在插值点比较密集的情况下。
②多项式插值法需要在每次迭代中重新计算多项式,这可能会增加计算成本。
③多项式插值法并不保证在所有情况下都能得到最优的线搜索步长。
④多项式插值法容易出现过拟合问题,特别是在使用高阶多项式时,可能导致计算结果不稳定。
⑤多项式插值法需要选择合适的插值节点,如果选择不合适的节点可能会导致插值多项式的误差很大。
⑥多项式插值法计算复杂度高,特别是当插值节点数目很多时,计算时间和内存开销都会很大。
综上所述,多项式插值法是一种可以应用于求解线搜索步长的方法,但需要在实际使用中仔细评估其适用性和精度,同时结合其它方法来提高计算的效率和准确性。在实际应用中,通常会优先考虑其他更加稳健和高效的方法,例如黄金分割法(0.618方法)或牛顿法等。
参考资料:
1、数值最优化方法(高立 编著)
2、机器人中的数值优化