一、BFS

• BFS 的关键点是状态的选取和标记。

1. BFS 简介

• BFS，其英文全称是 Breadth First Search，即广度优先算法。是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。
• BFS 属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。
• BFS 搜索时是一层一层的搜索的。可以用来解决最短路问题，是一个从近到远的扩散过程。
• BFS 主要应用于非加权图（或者所有边的权重相同，如若不相同的话则需采用其他的算法）中任两点的最短路径，寻找其中一个连通分支中的所有点。

2. BFS 的基本思想

• 从初始状态 S 开始，利用规则，生成所有可能的状态。
• 构成树的下一层节点，检查是否出现目标状态 G ，若未出现，就对该层所有状态节点，分别顺序利用规则，再生成下一层的所有状态节点，对这一层的所有状态节点检查是否出现 G 。
• 若未出现，继续按上面思想生成再下一层的所有状态节点，这样一层一层往下展开。
• 直到出现目标状态为止。

3. BFS 的实现步骤

• （1） 初始化队列和所求的值。
• （2） 判断是否为空并取出队头。
• （3） 利用队头去扩展。
• （4） 如果符合，将该点入队。
• 基本框架如下：

void bfs(){
	queue<int>q;
	q.push(初始位置);
	//初始化
	
	while(q.size()){
        int t = q.front();
        q.pop();//取出队头的点，用该点向周围扩散。
		if(check(j)){       //如果该点可行就将它加入队列中
        q.psuh(j);		
        //实施相应的操作 
        }
	} 
}

4. BFS 的实际演示

• BFS 在面临一个路口时，会把所有的岔路口都记下来，然后选择一个进入其中，把它的分离情况记录下来，然后再返回来进入另外一个岔路，并重复进行这样的操作。如下图所示：
• （1） 从黑色起点出发，记录所有的岔路口，并标记为走一步可以到达的。

• （2） 在此，我们选择黑色起点上方的路径，然后将这个路口可走的方向记录下来并标记为 2 ，意味着走两步可以到达的地方。

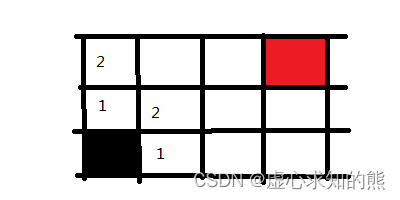
• （3） 随后，我们回到黑色起点右手边路径为 1 的方块上，并将其能走得方向也记录下来，同样标记为 2 ，因为也是走两步就可以到达的地方。

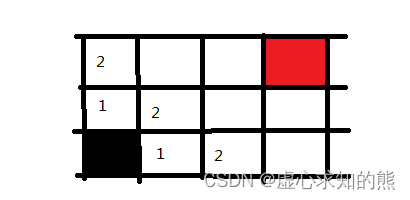
• （4） 此时，距离黑色起点路径为 1 和路径为 2 的方块就已经全都找到了。下面同理，我们可以迅速将路径为 3 的方块找到。

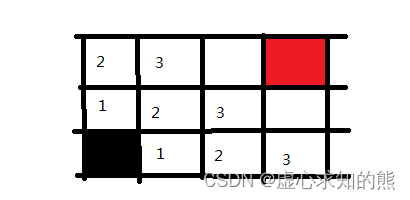
-（5） 后续，距离黑色起点路径为 4 和路径为 5 的方块也是同理。

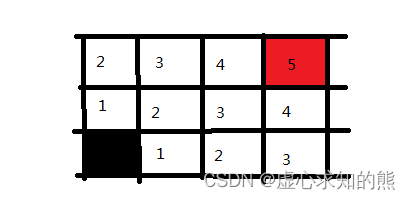
-（6） 通过如上步骤，我们便成功寻找到了路径，并且把所有可行的路径都求出来，

二、BFS 例题——走迷宫

题目描述

给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0 或 1，其中 0 表示可以走的路，1 表示不可通过的墙壁。
最初，有一个人位于左上角 (1,1) 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问，该人从左上角移动至右下角 (n,m) 处，至少需要移动多少次。
数据保证 (1,1) 处和 (n,m) 处的数字为 0，且一定至少存在一条通路。

输入格式

第一行包含两个整数 n 和 m。
接下来 n 行，每行包含 m 个整数（0 或 1），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围

1 ≤ n,m ≤ 100

输入样例

5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例

8

具体实现

1. 样例演示

• 具体演示如下图所示。
  

2. 实现思路

• 详细如样例演示所示。

3. 代码注解

• g[N][N]；存储地图，d[N][N]；存储起点到其他各个点的距离。
• queue q；用来存储每一步走到的点。
• while(!q.empty())；循环依次取出同一步数能走到的点，再往前走一步。
• int dx[4] = {0, 1, 0, -1},；dy[4] = {-1, 0, 1, 0}；一个点往下一步走得时候，可以往上下左右四方向走。

4. 实现代码

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;

const int N = 110;

int n, m;
int g[N][N], d[N][N];

int bfs()
{
    queue<PII> q;

    memset(d, -1, sizeof d);
    d[0][0] = 0;
    q.push({0, 0});

    int dx[4] = {-1, 0, 1, 0};
    int dy[4] = {0, 1, 0, -1};

    while (q.size())
    {
        auto t = q.front();
        q.pop();

        for (int i = 0; i < 4; i ++ )
        {
            int x = t.first + dx[i];
            int y = t.second + dy[i];

            if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
            {
                d[x][y] = d[t.first][t.second] + 1;
                q.push({x, y});
            }
        }
    }

    return d[n - 1][m - 1];
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
    {
        for (int j = 0; j < m; j ++ )
        {
            cin >> g[i][j];
        }
    }

    cout << bfs() << endl;
    system("pause");
    return 0;
}

三、BFS 例题——八数码

题目描述

在一个 3×3 的网格中，1∼8 这 8 个数字和一个 x 恰好不重不漏地分布在这 3×3 的网格中。
例如：

1 2 3
x 4 6
7 5 8

在游戏过程中，可以把 x 与其上、下、左、右四个方向之一的数字交换（如果存在）。
我们的目的是通过交换，使得网格变为如下排列（称为正确排列）：

1 2 3
4 5 6
7 8 x

例如，示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。
交换过程如下：

1 2 3
x 4 6
7 5 8

1 2 3
4 x 6
7 5 8

1 2 3
4 5 6
7 x 8

1 2 3
4 5 6
7 8 x

现在，给你一个初始网格，请你求出得到正确排列至少需要进行多少次交换。

输入格式

输入占一行，将 3×3 的初始网格描绘出来。
例如，如果初始网格如下所示：

1 2 3
x 4 6
7 5 8

则输入为：1 2 3 x 4 6 7 5 8

输出格式

输出占一行，包含一个整数，表示最少交换次数。
如果不存在解决方案，则输出 −1。

输入样例

2 3 4 1 5 x 7 6 8

输出样例

19

具体实现

1. 实现思路

• 暴力穷举。穷举出所有给定序列通过交换能得到的新序列，在穷举过程中保存交换次数。
• 在穷举过程中，如果出现了结果序列，就输出交换次数。否则不能得到结果序列，输出 -1。

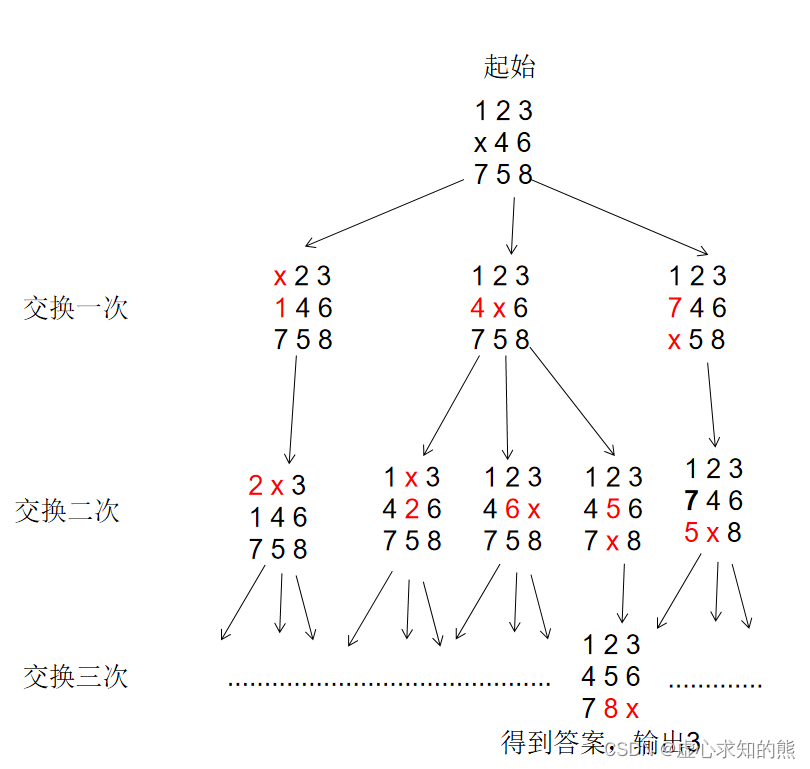
• 在此中间，我们可以使用字符串来表示表格中的状态，将 3x3 的数组表示成一行。
• 用一个队列保存当前获得的序列。
• 用一个哈希表保存各个序列与对应交换次数。

2. 代码注解

• int x = k / 3, y = k % 3；将一位数组的下标转换为二维数组。
• swap(t[a * 3 + b], t[k])；交换两次的原因是：for 循环是遍历 t 的上下左右四个点，swap 一下意味着 x y 和 a b 两个点换了位置，t 现在是 a b 。判断完 a b 之后还要从 x y 出发去遍历其他三个点，所以要还原一下。
• !d.count(t)；是来判断这个点是否为有效点。因为要找到最短距离，要是不为零的话意味着用之前的换法已经换到这个状态过了，用现在这个状态接着换还不如接着以前的状态换，以前的步数还少一些，而且这样才能把所有可能换到的状态全部枚举一遍。

3. 实现代码

#include <bits/stdc++.h>
using namespace std;

int bfs(string state)
{
    queue<string> q;
    unordered_map<string, int> d;

    q.push(state);
    d[state] = 0;

    int dx[4] = {-1, 0, 1, 0};
    int dy[4] = {0, 1, 0, -1};

    string end = "12345678x";
    while (q.size())
    {
        auto t = q.front();
        q.pop();

        if (t == end) 
        {
            return d[t];
        }

        int distance = d[t];
        int k = t.find('x');
        int x = k / 3, y = k % 3;
        for (int i = 0; i < 4; i ++ )
        {
            int a = x + dx[i];
            int b = y + dy[i];
            if (a >= 0 && a < 3 && b >= 0 && b < 3)
            {
                swap(t[a * 3 + b], t[k]);
                if (!d.count(t))
                {
                    d[t] = distance + 1;
                    q.push(t);
                }
                swap(t[a * 3 + b], t[k]);
            }
        }
    }

    return -1;
}

int main()
{
    char s[2];

    string state;
    for (int i = 0; i < 9; i ++ )
    {
        cin >> s;
        state += *s;
    }

    cout << bfs(state) << endl;

    return 0;
}