L-shape 方法是求解两阶段随机规划的一种常用方法，基本思想是利用切平面将第二阶段的反馈函数线性化，在构造切平面条件时有点类似 bender’s 方法。

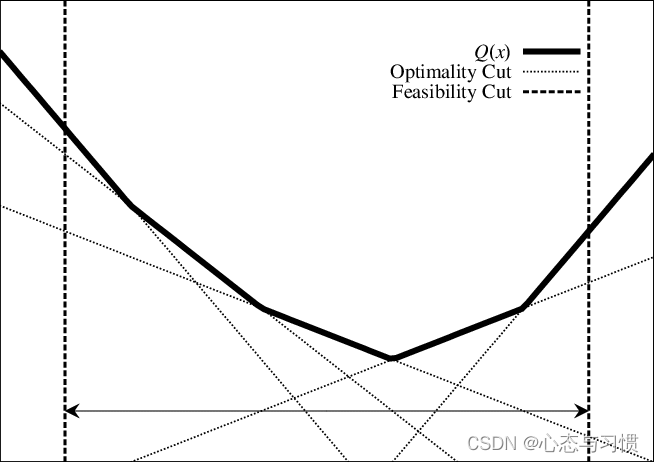
注：这个图形中黑实线 $\mathcal{Q}(x)$ 就是下面模型中的 $\mathcal{L}(x)$

两阶段随机规划的模型可以表示为：

$$\begin{array}{rlrl}& \underset{x}{\min }& & c^{T}x+\mathcal{L}(x)\\ & s.t.& & \\ & & & Ax=b\\ & & & x\ge 0\end{array}$$

其中，$\mathcal{L}(x)=\mathbb{E}[Q(x,\xi (\omega ))]$，被称作反馈函数 (recourse function)，而 $Q(x,\xi (\omega ))$ 为给定 $x$ 与 $\omega$ 时，第二段模型的最优值，即：

$$\begin{array}{rlrl}& & & Q(x,\xi (\omega ))=\underset{y}{\min }q(\omega {)}^{T}y\\ s.t.& & & \\ & & & T(\omega )x+Wy=h(\omega )\\ & & & y\ge 0\end{array}$$

模型中，$x$ 为第一阶段的决策变量，必须在不确定性发生之前作出决定，$y$ 为第二阶段的决策变量，在不确定性发生之后作出决定。$\xi$ 为随机变量，而 $\omega$ 为随机变量的一个具体实现值，模型中的决策变量与随机变量都可以是向量形式。

上面第二个模型中，可以看出 $W$ 与 $\omega$ 无关，即第二阶段求解变量 $y$ 的系数是一个确定值，并不是随机变量。此时，上面两个模型称作固定反馈 (fixed recourse) 的两阶段随机规划模型。因为固定反馈时，第二阶段模型 $x$ 的可行域为一个闭凸集，这样就能使用很多方法求解了，否则第二阶段模型 $x$ 的可行域不一定是闭凸集（为什么？目前还没搞清楚）。

假设随机变量 $\xi$ 具有有限个，即 $K$ 个实现值（realization），每个实现值对应的概率为 $p_k$，则两阶段规划的扩展模型（extensive form）可以表示为：

$$\begin{array}{rlrl}& \underset{x}{\min }& & c^{T}x+\sum _{k=1}^K{p}_k{q}_k^T{y}_k\\ & s.t.& & \\ & & & Ax=b\\ & & & T_{k}x+W{y}_k=h_k,k=1,\dots ,K,\\ & & & x\ge 0,y_k\ge 0,k=1,\dots ,K.\end{array}$$

为什么叫 L-shaped 方法，是因为前两个约束条件左端的系数矩阵可以写成类似 L 的形式：

$$\begin{array}{rl}& A\\ & T_{1}W\\ & T_{2}W\\ & ⋮\\ & T_k\dots \dots W\end{array}$$

L-shape 方法的基本步骤是：

• 给定第一阶段求解变量 $x$ 的一个初始值，带入到第二阶段的模型进行求解
• 若有可行解，根据第二阶段的对偶值，计算出最优性切平面约束（optimality cut）添加到第一阶段的模型中
• 若无可行解，根据另外一个构造的线性规划模型（以后补充）求出可行性约束（feasibility cut）添加到第一阶段模型中
• 求解第一阶段模型，返回第一步
• 循环以上过程，直到达到一定的迭代终止条件

未完待续。。