⭐️前言⭐️
本篇文章主要介绍图及其与图相关的算法
🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁
🍉博主将持续更新学习记录收获,友友们有任何问题可以在评论区留言
🍉博客中涉及源码及博主日常练习代码均已上传GitHub

📍内容导读📍
- 🍅图概念
- 🍅图的表达方式
- 🍅图的抽象数据结构
- 🍅图的宽度优先遍历 BFS
- 🍅图的深度优先遍历 DFS
- 🍅图的拓扑排序
- 🍅最小生成树算法Kruskal
- 🍅最小生成树算法Prim
- 🍅单元最短路径算法Dijkstra
🍅图概念
1)由点的集合和边的集合构成
2)虽然存在有向图和无向图(无向a-b相当于有向,边是相互的)的概念,但实际上都可以用有向图来表达
3)边上可能带有权重
🍅图的表达方式
1)邻接表法

2)邻接矩阵法
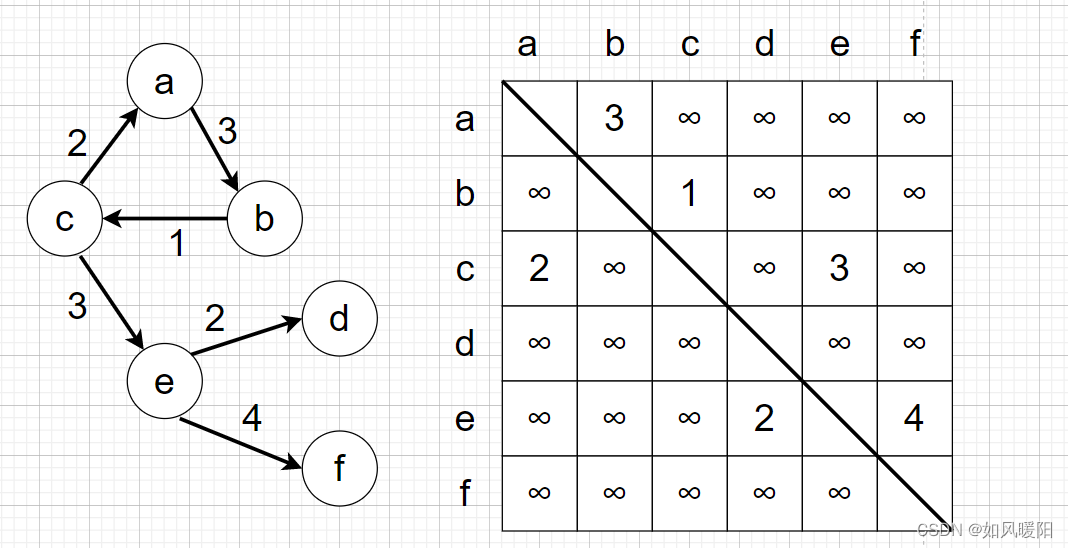
以上两种是教科书上的讲法,实际题目中通常不以以上形式出现,而是以下这种方式:
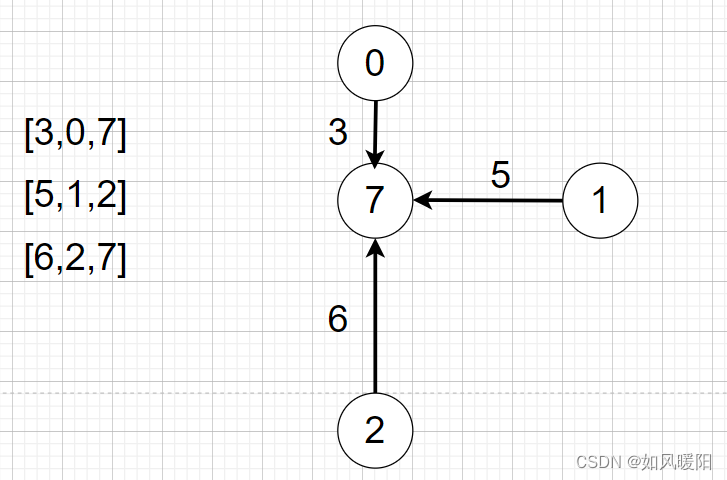
甚至一个数组也能表示一个图结构。
🍅图的抽象数据结构
因为图有多种不同的表达方式,所以为了解题,我们可以抽象出一种图结构,在得到不同的图的表达方式后,转换到我们自己熟悉的图结构上,用模板来完成解题。
以下就是抽象出来的图结构的代码:
首先是点结构的描述:
public class Node {
public int value;
public int in; // 入度:表示有多少个节点指向该节点
public int out; // 出度:表示该节点指向了多少个节点
public ArrayList<Node> nexts; // 存储该节点直接指向节点的集合
public ArrayList<Edge> edges; // 存储该节点直接访问的边的集合
public Node(int value) {
this.value=value;
in=0;
out=0;
nexts=new ArrayList<>();
edges=new ArrayList<>();
}
}
边结构的描述:
public class Edge {
public int weight; // 边的权重(距离长度)
public Node from; // 边的起始节点
public Node to; // 边的终止节点
public Edge(int weight, Node from, Node to) {
this.weight = weight;
this.from = from;
this.to = to;
}
}
图结构的描述:
public class Graph {
public HashMap<Integer,Node> nodes;
public HashSet<Edge> edges;
public Graph() {
nodes=new HashMap<>();
edges=new HashSet<>();
}
}
生成图:
public class GraphGenerator {
/*
输入N*3的矩阵
[5,0,7]
[3,0,1]
......
[weight,from节点上面的值,to节点上面的值]
*/
public static Graph createGraph(int[][] matrix) {
Graph graph=new Graph();
for (int i = 0; i < matrix.length; i++) {
int weight=matrix[i][0];
int from=matrix[i][1];
int to=matrix[i][2];
if(!graph.nodes.containsKey(from)) {
graph.nodes.put(from,new Node(from));
}
if(!graph.nodes.containsKey(to)) {
graph.nodes.put(to,new Node(to));
}
Node fromNode=graph.nodes.get(from);
Node toNode=graph.nodes.get(to);
Edge newEdge=new Edge(weight,fromNode,toNode);
fromNode.nexts.add(toNode);
fromNode.out++;
toNode.in++;
fromNode.edges.add(newEdge);
graph.edges.add(newEdge);
}
return graph;
}
}
🍅图的宽度优先遍历 BFS
1、利用队列实现(与二叉树BFS类似)
2、从源节点开始依次把邻节点进队列,然后弹出(弹出时打印节点)
3、每弹出一个点,把该节点所有没有进过队列的邻结点入队列
4、直到队列为空
代码实现:
public class BFS {
public static void bfs(Node start) {
if(start==null) {
return;
}
Queue<Node> queue=new LinkedList<>();
HashSet<Node> set=new HashSet<>();
queue.add(start);
set.add(start);
while (!queue.isEmpty()) {
Node cur=queue.poll();
System.out.println(cur.value);
for(Node next: cur.nexts) {
if(!set.contains(next)) {
queue.offer(next);
set.add(next);
}
}
}
}
}
🍅图的深度优先遍历 DFS
1、利用栈实现(栈记录遍历的路径)
2、从源节点开始把节点按深度放入栈,然后弹出
3、每弹出一个点,就把该节点下一个没有进过栈的邻节点放入栈(入栈后打印节点)
4、直到栈为空
代码实现:
public class DFS {
public static void dfs(Node start) {
if(start==null) {
return;
}
Stack<Node> stack=new Stack<>();
HashSet<Node> set=new HashSet<>();
stack.add(start);
set.add(start);
System.out.println(start.value);
while (!stack.isEmpty()) {
Node cur=stack.pop();
for(Node next: cur.nexts) {
if(!set.contains(next)) {
stack.push(cur);
stack.push(next);
set.add(next);
System.out.println(next.value);
break;
}
}
}
}
}
🍅图的拓扑排序
常见的应用场景是编译排序、事件安排:
比如包A需要包B、C,包B需要包D,包C需要包E、F,如果想要加载好包A,首先需要加载D得到B,加载E、F得到C,再通过B、C得到A。
想要实现拓扑排序,就需要按照以下步骤操作:
1)在图中找到所有入度为0的点(拓扑序的起始处)输出
2)把所有入度为0的点在图中删掉,继续找入度为0的点输出,周而复始
3)图的所有点都被删除后,依次输出的顺序就是拓扑排序。
要求:有向图且其中无环
代码实现:
public class TopologySort {
public static List<Node> sortedTopology(Graph graph) {
// key:某个节点 value:剩余的入度
HashMap<Node,Integer> inMap=new HashMap<>();
// 只有剩余入度为0的点,才进入这个队列
Queue<Node> zeroInQueue=new LinkedList<>();
for(Node node:graph.nodes.values()) {
inMap.put(node, node.in);
if(node.in==0) {
zeroInQueue.offer(node);
}
}
List<Node> result=new ArrayList<>();
while (!zeroInQueue.isEmpty()) {
Node cur=zeroInQueue.poll();
result.add(cur);
for (Node next: cur.nexts) {
inMap.put(next,inMap.get(next)-1);
if(inMap.get(next)==0) {
zeroInQueue.offer(next);
}
}
}
return result;
}
}
题目练习:https://www.lintcode.com/problem/127/

BFS解法:
与演示代码思想类似,利用入度为0的节点做为解题点。
public class TopologicalOrderBFS {
// 不提交该类
public static class DirectedGraphNode {
public int label;
public ArrayList<DirectedGraphNode> neighbors;
public DirectedGraphNode(int label) {
this.label = label;
neighbors=new ArrayList<>();
}
}
// 提交以下代码
public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
HashMap<DirectedGraphNode,Integer> indegreeMap=new HashMap<>();
for (DirectedGraphNode cur:graph) {
indegreeMap.put(cur,0);
}
for (DirectedGraphNode cur:graph) {
for (DirectedGraphNode next: cur.neighbors) {
indegreeMap.put(next,indegreeMap.get(next)+1);
}
}
Queue<DirectedGraphNode> zeroQueue=new LinkedList<>();
for (DirectedGraphNode cur:indegreeMap.keySet()) {
if(indegreeMap.get(cur)==0) {
zeroQueue.offer(cur);
}
}
ArrayList<DirectedGraphNode> result=new ArrayList<>();
while (!zeroQueue.isEmpty()) {
DirectedGraphNode cur=zeroQueue.poll();
result.add(cur);
for(DirectedGraphNode next: cur.neighbors) {
indegreeMap.put(next,indegreeMap.get(next)-1);
if(indegreeMap.get(next)==0) {
zeroQueue.offer(next);
}
}
}
return result;
}
}
DFS解法:
解法1:根据一个节点可以到达节点的节点次来比较拓扑序
public class TopologicalOrderDFS1 {
// 不提交该类
public static class DirectedGraphNode {
public int label;
public ArrayList<DirectedGraphNode> neighbors;
public DirectedGraphNode(int label) {
this.label = label;
neighbors=new ArrayList<>();
}
}
// 提交以下的
/**
* 该类用于记录每个节点可以访问的节点次,越大拓扑序越靠前
*/
public static class Record {
public DirectedGraphNode node;
public long nodes;
public Record(DirectedGraphNode node, long nodes) {
this.node = node;
this.nodes = nodes;
}
}
public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
HashMap<DirectedGraphNode,Record> order=new HashMap<>();
for(DirectedGraphNode cur:graph) {
f(cur,order);
}
ArrayList<Record> records=new ArrayList<>();
for(Record r:order.values()) {
records.add(r);
}
records.sort(new Comparator<Record>() {
@Override
public int compare(Record o1, Record o2) {
return o1.nodes == o2.nodes ? 0 : (o1.nodes > o2.nodes ? -1 : 1);
}
});
ArrayList<DirectedGraphNode> result=new ArrayList<>();
for (Record r:records) {
result.add(r.node);
}
return result;
}
// 返回cur节点可到的所有节点次
public static Record f(DirectedGraphNode cur,HashMap<DirectedGraphNode,Record> order) {
if(order.containsKey(cur)) {
return order.get(cur);
}
long nodes=0;
for(DirectedGraphNode next: cur.neighbors) {
nodes+=f(next,order).nodes;
}
Record ans=new Record(cur,nodes+1);
order.put(cur,ans);
return ans;
}
}
解法2: 根据一个节点可以到达的最大深度来比较拓扑序
public class TopologicalOrderDFS2 {
// 不要提交这个类
public static class DirectedGraphNode {
public int label;
public ArrayList<DirectedGraphNode> neighbors;
public DirectedGraphNode(int x) {
label = x;
neighbors = new ArrayList<DirectedGraphNode>();
}
}
// 提交下面的
public static class Record {
public DirectedGraphNode node;
public int deep;
public Record(DirectedGraphNode node, int deep) {
this.node = node;
this.deep = deep;
}
}
public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
HashMap<DirectedGraphNode,Record> order=new HashMap<>();
for(DirectedGraphNode cur:graph) {
f(cur,order);
}
ArrayList<Record> records=new ArrayList<>();
for(Record r:order.values()) {
records.add(r);
}
records.sort(new Comparator<Record>() {
@Override
public int compare(Record o1, Record o2) {
return o2.deep- o1.deep;
}
});
ArrayList<DirectedGraphNode> result=new ArrayList<>();
for(Record r:records) {
result.add(r.node);
}
return result;
}
public static Record f(DirectedGraphNode cur,HashMap<DirectedGraphNode,Record> order) {
if(order.containsKey(cur)) {
return order.get(cur);
}
int follow=0;
for(DirectedGraphNode next: cur.neighbors) {
follow=Math.max(follow,f(next,order).deep);
}
Record ans=new Record(cur,follow+1);
order.put(cur,ans);
return ans;
}
}
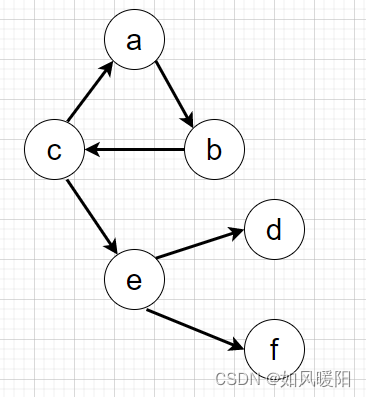
🍅最小生成树算法Kruskal
最小生成树一定是无向图
该算法就是求可以遍历到所有节点的最小权值边的集合,如下图所示,无向图(图左)的最小生成树就是图右
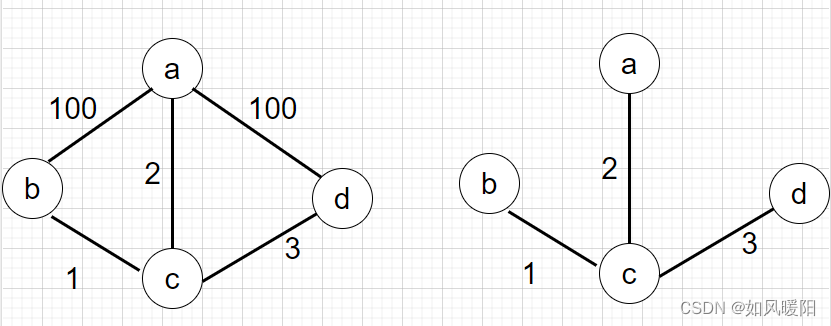
通过并查集(点)+优先级队列(边权值)来解
算法设计思想总结如下:
1)总是从权值小的边开始考虑,依次考察权值依次变大的边(借助优先级队列)
2)当前的边要么进入最小生成树的集合,要么丢弃
3)如果当前的边进入最小生成树的集合中不会形成环,就要当前边(借助并查集判断是否成环)
4)如果当前的边进入最小生成树的集合中会形成环,就不要当前边
5)考察完所有的边之后,最小生成树的集合也就得到了
因为要求最小生成树,所以首先从权值小的边开始考虑;如果有环,说明该边可以连接的节点,可以通过其他边实现,又因为是从权值小的开始考虑的,所以该边舍弃;
判断是否有环可以通过并查集,判断点所在集合是否是同一个集合即可判断是否有环。
代码实现:
public class Kruskal {
public static class UnionFind {
// key:某个节点 value:key节点的代表节点
private HashMap<Node,Node> representMap;
// key:某个集合的代表节点 value:key所在集合的节点个数
private HashMap<Node,Integer> sizeMap;
public UnionFind(Graph graph) {
representMap=new HashMap<>();
sizeMap=new HashMap<>();
for (Node node:graph.nodes.values()) {
representMap.put(node,node);
sizeMap.put(node,1);
}
}
private Node findRepresent(Node x) {
Stack<Node> path=new Stack<>();
while (x!=representMap.get(x)) {
path.add(x);
x=representMap.get(x);
}
while (!path.isEmpty()) {
representMap.put(path.pop(),x);
}
return x;
}
public boolean isSameSet(Node a,Node b) {
return findRepresent(a)==findRepresent(b);
}
public void union(Node a,Node b) {
if(a==null||b==null) {
return;
}
Node fa=findRepresent(a);
Node fb=findRepresent(b);
if(fa!=fb) {
int aSetSize=sizeMap.get(fa);
int bSetSize=sizeMap.get(fb);
if(aSetSize>=bSetSize) {
representMap.put(fb,fa);
sizeMap.put(fa,aSetSize+bSetSize);
sizeMap.remove(fb);
}else {
representMap.put(fa,fb);
sizeMap.put(fb,aSetSize+bSetSize);
sizeMap.remove(fa);
}
}
}
}
public static Set<Edge> kruskal(Graph graph) {
UnionFind unionFind=new UnionFind(graph);
// 默认小根堆
PriorityQueue<Edge> priorityQueue=new PriorityQueue<>(new Comparator<Edge>() {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight-o2.weight;
}
});
for (Edge edge:graph.edges) {
priorityQueue.add(edge);
}
Set<Edge> result=new HashSet<>();
while (!priorityQueue.isEmpty()) {
Edge edge=priorityQueue.poll();
if(!unionFind.isSameSet(edge.from,edge.to)) {
result.add(edge);
unionFind.union(edge.from,edge.to);
}
}
return result;
}
}
🍅最小生成树算法Prim
点解锁边,边解锁点
小根堆(解锁的边)+哈希Set(被解锁的点)
1)可以从任意节点出发来寻找最小生成树
2)某个点被加入到解锁点集合后,解锁这个点出发的所有新的边
3)在所有解锁的边中选取最小的边,然后看看这个边会不会形成环(就是该边连接的节点是不是已经被解锁过了)
4)如果会,不要当前边,继续考察剩下解锁的边中最小的边,重复3
5)如果不会,要当前边,将该边指向的节点加入到被选取的点中,重复2
6)当所有的点被选取后,最小生成树就得到了。
代码实现:
public class Prim {
public static Set<Edge> prim(Graph graph) {
// 解锁的边进入小根堆
PriorityQueue<Edge> priorityQueue=new PriorityQueue<>(new Comparator<Edge>() {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight- o2.weight;
}
});
// 解锁的点进入set集合
HashSet<Node> nodeSet=new HashSet<>();
Set<Edge> result=new HashSet<>();
for (Node node:graph.nodes.values()) { // 随便挑了一个点
if(!nodeSet.contains(node)) {
nodeSet.add(node);
for(Edge edge:node.edges) { // 由一个点解锁所有相连边
priorityQueue.add(edge);
}
while (!priorityQueue.isEmpty()) {
Edge edge=priorityQueue.poll();// 弹出解锁的边中,最小的边
Node toNode=edge.to;
if(!nodeSet.contains(toNode)) {
nodeSet.add(toNode);
result.add(edge);
for(Edge nextEdge: toNode.edges) {
priorityQueue.add(nextEdge);
}
}
}
}
// break
}
return result;
}
}
🍅单元最短路径算法Dijkstra
必须是有向无负权重的图,一定是要给定一个出发点,要求的是从出发点到所有可到达点的最短距离的一张表。
1)必须指定源点
2)生成一个源点到各个点的最小距离表,一开始只有一条记录,及源点到自己的距离为0,到其他点的距离为正无穷
3)从距离表中拿出没选过点里的最小记录,通过这个点发出的边,更新源点到各个点的最小距离表,不断重复这一步
4)源点到所有的点的记录如果都被拿过一遍,过程停止,最小距离表拿到了
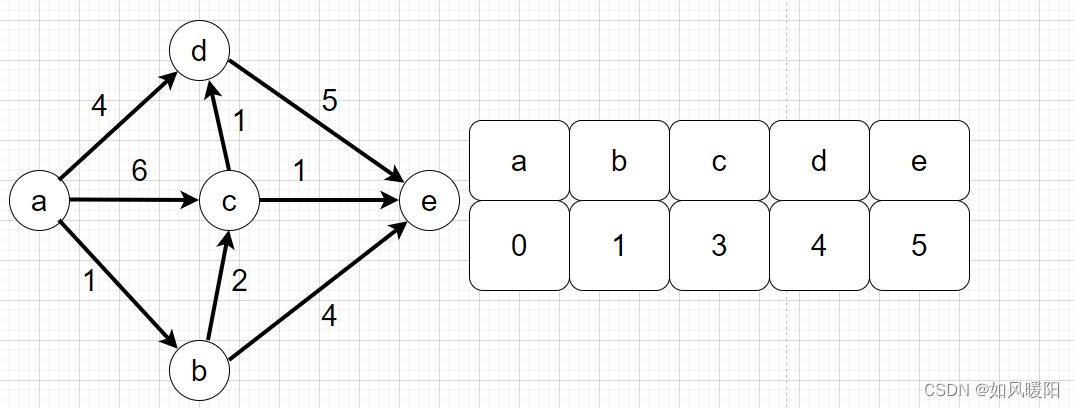
代码实现:
public class Dijkstra {
public static HashMap<Node,Integer> dijkstra(Node from) {
HashMap<Node,Integer> distanceMap=new HashMap<>();// 距离表
distanceMap.put(from,0);
// 被选择过的点
HashSet<Node> selectedNodes=new HashSet<>();
Node minNode=getMinDistanceAndUnselectedNode(distanceMap,selectedNodes);
while (minNode!=null) {
// 原始点 -> minNode(跳转点) 最小距离 distance
int distance=distanceMap.get(minNode);
for(Edge edge: minNode.edges) {
Node toNode=edge.to;
if(!distanceMap.containsKey(toNode)) {
distanceMap.put(toNode,distance+edge.weight);
}else {
distanceMap.put(edge.to,Math.min(distanceMap.get(toNode),distance+edge.weight));
}
}
selectedNodes.add(minNode);
minNode=getMinDistanceAndUnselectedNode(distanceMap,selectedNodes);
}
return distanceMap;
}
private static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> distanceMap, HashSet<Node> selectedNodes) {
Node minNode=null;
int minDistance=Integer.MAX_VALUE;
for(Map.Entry<Node,Integer> entry:distanceMap.entrySet()) {
Node node=entry.getKey();
int distance= entry.getValue();
if(!selectedNodes.contains(node)&&distance<minDistance) {
minNode=node;
minDistance=distance;
}
}
return minNode;
}
}
加强堆实现优化:
由于普通方法需要每次都获取未被选择且距离最小的点,方法实现较为繁琐,可以通过借助加强堆来实现。
直接在堆上实现节点记录类的增加和修改。
代码实现:
public class Dijkstra {
public static class NodeRecord {
public Node node;
public int distance;
public NodeRecord(Node node, int distance) {
this.node = node;
this.distance = distance;
}
}
public static class NodeHeap {
private Node[] nodes;// 实际的堆结构
// key:某个node value:上面堆中的位置
private HashMap<Node,Integer> heapIndexMap;// 反向索引表
// key:某个节点 value:从源节点触发到该节点的目前最小距离
private HashMap<Node,Integer> distanceMap;
private int size;// 堆上有多少个点
public NodeHeap(int size) {
nodes=new Node[size];
heapIndexMap=new HashMap<>();
distanceMap=new HashMap<>();
size=0;
}
public boolean isEmpty() {
return size==0;
}
public void addOrUpdateOrIgnore(Node node,int distance) {
if(inHeap(node)) { // update
distanceMap.put(node,Math.min(distanceMap.get(node),distance));
heapInsert(heapIndexMap.get(node));
}
if(!isEntered(node)) { // add
nodes[size]=node;
heapIndexMap.put(node,size);
distanceMap.put(node,distance);
heapInsert(size++);
}
// ignore
}
public NodeRecord pop() {
NodeRecord nodeRecord=new NodeRecord(nodes[0],distanceMap.get(nodes[0]));
swap(0,size-1);
heapIndexMap.put(nodes[size-1],-1);
distanceMap.remove(nodes[size-1]);
nodes[size-1]=null;
shiftDown(0,--size);
return nodeRecord;
}
private void heapInsert(int child) {
int parent=(child-1)/2;
while (child>0) {
if(distanceMap.get(child)<distanceMap.get(parent)) {
swap(child,parent);
child=parent;
parent=(child-1)/2;
}else {
break;
}
}
}
private void shiftDown(int parent,int size) {
int child=parent*2+1;
while (child<size) {
if(child+1<size&&distanceMap.get(child)>distanceMap.get(child+1)) {
child++;
}
if(distanceMap.get(child)<distanceMap.get(parent)) {
swap(child,parent);
parent=child;
child=2*parent+1;
}else {
break;
}
}
}
private void swap(int index1,int index2) {
heapIndexMap.put(nodes[index1],index2);
heapIndexMap.put(nodes[index2],index1);
Node tmp=nodes[index1];
nodes[index1]=nodes[index2];
nodes[index2]=tmp;
}
private boolean isEntered(Node node) {
return heapIndexMap.containsKey(node);
}
private boolean inHeap(Node node) {
return isEntered(node)&&heapIndexMap.get(node)!=-1;
}
}
// 改进后的dijkstra算法
// 从head出发,所有head能到达的节点,生成到达每个的路径记录并返回
public static HashMap<Node,Integer> dijkstra(Node head,int size) {
NodeHeap nodeHeap=new NodeHeap(size);
nodeHeap.addOrUpdateOrIgnore(head,0);
HashMap<Node,Integer> result=new HashMap<>();
while (!nodeHeap.isEmpty()) {
NodeRecord record=nodeHeap.pop();
Node cur=record.node;
int distance=record.distance;
for(Edge edge: cur.edges) {
nodeHeap.addOrUpdateOrIgnore(edge.to,edge.weight+distance);
}
result.put(cur,distance);
}
return result;
}
}
⭐️最后的话⭐️
总结不易,希望uu们不要吝啬你们的👍哟(^U^)ノ~YO!!如有问题,欢迎评论区批评指正😁