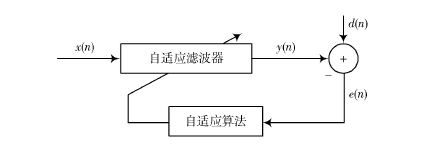
自适应滤波器
-
自适应滤波器:一种能够根据输入信号自动调整自身参数的数字滤波器
-
非自适应滤波器:具有静态滤波器系统的数字滤波器,静态系数构成了滤波器的传递函数
-
对于一些应用(如系统辨识、预测、去噪等),无法事先知道需要操作的参数,必须使用自适应的系数进行处理,这种情况下通常使用自适应滤波器
-
自适应滤波器处理语音信号时,不需要实现知道输入信号和噪声的统计特性,滤波器自身能够在工作过程中学习或估计信号的统计特性,并以此为依据调整自身参数,以达到某种准则/代价函数下的最优滤波效果
-
自适应滤波器是处理非平稳信号的一种有效手段
-
下面从一个N阶的滤波器出发,逐步过渡到自适应滤波器
N阶滤波器
- 一个N阶滤波器,参数为 w ( n ) \text{w}(n) w(n),包含N个独立的滤波器系数
- 滤波器的输出为输入信号和滤波器系数的线性卷积:
y ( n ) = ∑ i = 0 N − 1 w i ( n ) x ( n − i ) = w T ( n ) x ( n ) = x T ( n ) w ( n ) y(n)=\sum_{i=0}^{N-1}w_i(n)x(n-i)=\text{w}^T(n)\text{x}(n)=\text{x}^T(n)\text{w}(n) y(n)=i=0∑N−1wi(n)x(n−i)=wT(n)x(n)=xT(n)w(n) - 其中,
- x ( n ) = [ x ( n ) , x ( n − 1 ) , . . . , x ( n − N + 1 ) ] T \text{x}(n)=[x(n),x(n-1),...,x(n-N+1)]^T x(n)=[x(n),x(n−1),...,x(n−N+1)]T
- w ( n ) = [ w 0 ( n ) , w 1 ( n ) , . . . , w N − 1 ( n ) ] T \text{w}(n)=[w_0(n),w_1(n),...,w_{N-1}(n)]^T w(n)=[w0(n),w1(n),...,wN−1(n)]T
- 括号里的n表示不同的时刻
- 定义期望输出为d(n),误差序列为: e ( n ) = d ( n ) − y ( n ) = d ( n ) − w T ( n ) x ( n ) e(n)=d(n)-y(n)=d(n)-\text{w}^T(n)\text{x}(n) e(n)=d(n)−y(n)=d(n)−wT(n)x(n)
- 由于n时刻的误差是根据n时刻的滤波器系数进行定义的,因此该误差被称为“后验误差”
标准LMS算法
- 根据最小化均方误差(MMSE)准则,最小化目标函数为
J ( w ) = E [ ∣ e ( n ) ∣ 2 ] = E [ ∣ d ( n ) − w T ( n ) x ( n ) ∣ 2 ] J(\text{w})=E[|e(n)|^2]=E[|d(n)-\text{w}^T(n)\text{x}(n)|^2] J(w)=E[∣e(n)∣2]=E[∣d(n)−wT(n)x(n)∣2] - 为了最小化均方误差函数,需计算
J
(
w
)
J(\text{w})
J(w)对w的导数,令导数为零:
E [ x ( n ) x T ( n ) ] w ( n ) − E [ x ( n ) d ( n ) ] = R w − r = 0 E[\text{x}(n)\text{x}^T(n)]\text{w}(n)-E[\text{x}(n)d(n)]=R\text{w}-r=0 E[x(n)xT(n)]w(n)−E[x(n)d(n)]=Rw−r=0 - 可得到: w o p t = R − 1 r \text{w}_{opt}=R^{-1}r wopt=R−1r
- 称 w o p t \text{w}_{opt} wopt定义的滤波器为Wiener滤波器,Wiener滤波器是均方误差最小意义上的统计最优滤波器
- Wiener滤波器的缺陷:
- 不适用于非平稳过程,而语音就是非平稳信号
- 数学期望的计算需要利用全部的历史数据,来估计当前的滤波器系数,这不是合理的选择
- 由于涉及数学期望,在实际应用中,无法获得信号真实的自相关矩阵R,以及输入信号和期望输出之前的互相关向量r。因此,在实际应用中,利用瞬时误差的平方代替目标函数中的数学期望,再求取瞬时梯度:
▽
(
n
)
=
−
2
e
(
n
)
x
(
n
)
\triangledown (n)=-2e(n)\text{x}(n)
▽(n)=−2e(n)x(n),然后沿着负梯度方向更新滤波器系数:
w ( n + 1 ) = w ( n ) + 2 μ x ( n ) e ( n ) \text{w}(n+1)=\text{w}(n)+2\mu \text{x}(n)e(n) w(n+1)=w(n)+2μx(n)e(n) - 上式为标准时序LMS算法的更新公式,为逐点更新,每当给定一个新的x(n)和d(n),滤波器系数就更新一次
- 标准LMS算法的执行流程:
- 初始化w(0)、x(0)
- 对每一个新的输入值x(n),计算输出值y(n)
- 利用期望输出d(n),计算误差值e(n),从而得到梯度
- 更新滤波器系数,得到w(n+1)
- 返回步骤2,直至结束,可得到输出序列和误差序列
- 标准LMS算法
- 基本思想是梯度下降
- 优点是算法简单,易实现
- 缺点是收敛速度慢,因为存在梯度噪声,所以跟踪性能比较差
block(分块)LMS算法
- 用更多采样点,更新一次滤波器系数:
w ( n + 1 ) = w ( n ) + 2 μ x ( n ) e ( n ) w ( n + 2 ) = w ( n + 1 ) + 2 μ x ( n + 1 ) e ( n + 1 ) . . . w ( n + L ) = w ( n + L − 1 ) + 2 μ x ( n + L − 1 ) e ( n + L − 1 ) \begin{aligned} \text{w}(n+1)&=\text{w}(n)+2\mu \text{x}(n)e(n) \\ \text{w}(n+2)&=\text{w}(n+1)+2\mu \text{x}(n+1)e(n+1) \\ ... \\ \text{w}(n+L)&=\text{w}(n+L-1)+2\mu \text{x}(n+L-1)e(n+L-1) \end{aligned} w(n+1)w(n+2)...w(n+L)=w(n)+2μx(n)e(n)=w(n+1)+2μx(n+1)e(n+1)=w(n+L−1)+2μx(n+L−1)e(n+L−1) - 得: w ( n + L ) = w ( n ) + 2 μ ∑ m = 0 L − 1 x ( n + m ) e ( n + m ) \text{w}(n+L)=\text{w}(n)+2\mu \sum_{m=0}^{L-1} \text{x}(n+m)e(n+m) w(n+L)=w(n)+2μ∑m=0L−1x(n+m)e(n+m)
- 分块更新,每L点更新一次滤波器系数
- 注意,误差序列是通过同一个滤波器得到的: e ( n + m ) = d ( n + m ) − x T ( n + m ) w ( n ) e(n+m)=d(n+m)-\text{x}^T(n+m)\text{w}(n) e(n+m)=d(n+m)−xT(n+m)w(n)
- 为了后续推到方便,令L=N,也就是说收集到采样点个数等于滤波器阶数时,才进行滤波器系数更新
- 与标准LMS相比,block LMS的更新频率降低了L倍,因此定义一个新的时间索引k来代替n, k = n L k=\frac{n}{L} k=Ln
- 从而block LMS更新公式为: w ( k + 1 ) = w ( k ) + 2 μ ∑ m = 0 L − 1 x ( k L + m ) e ( k L + m ) \text{w}(k+1)=\text{w}(k)+2\mu \sum_{m=0}^{L-1} \text{x}(kL+m)e(kL+m) w(k+1)=w(k)+2μ∑m=0L−1x(kL+m)e(kL+m)
- block LMS中,瞬时梯度为: ▽ ( k ) = − 2 ∑ m = 0 L − 1 x ( k L + m ) e ( k L + m ) \triangledown (k)=-2 \sum_{m=0}^{L-1} \text{x}(kL+m) e(kL+m) ▽(k)=−2∑m=0L−1x(kL+m)e(kL+m)
- block LMS的核心运算:
- 输出序列为输入信号与滤波器系数的线性卷积: y ( n + m ) = x T ( n + m ) w ( n ) , m ∈ [ 0 , N − 1 ] y(n+m)=\text{x}^T(n+m)\text{w}(n),m \in [0,N-1] y(n+m)=xT(n+m)w(n),m∈[0,N−1]
- 瞬时梯度为输入信号与误差序列的线性相关: ▽ ( k ) = − 2 ∑ m = 0 L − 1 x ( k L + m ) e ( k L + m ) \triangledown (k)=-2 \sum_{m=0}^{L-1} \text{x}(kL+m) e(kL+m) ▽(k)=−2∑m=0L−1x(kL+m)e(kL+m)
- 利用FFT计算线性卷积的方法有Overlap-save method和Overlap-add method
Overlap-save method
-
线性卷积与圆周卷积的关系:一般地,如果两个有限长序列的长度为 N 1 、 N 2 N_1、N_2 N1、N2,且满足 N 1 ≥ N 2 N_1 \ge N_2 N1≥N2,则圆周卷积的后 N 1 − N 2 + 1 N_1-N_2+1 N1−N2+1个点,与线性卷积的结果一致
-
线性相关与圆周相关的关系:一般地,如果两个有限长序列的长度为 N 1 、 N 2 N_1、N_2 N1、N2,且满足 N 1 ≥ N 2 N_1 \ge N_2 N1≥N2,则圆周相关的前 N 1 − N 2 + 1 N_1-N_2+1 N1−N2+1个点,与线性相关的结果一致
-
希望理解上述两个关系,可参考数字信号的基本运算——线性卷积(相关)和圆周卷积(相关)
-
为了得到N个点的输出序列: y ( n + m ) = x T ( n + m ) w ( n ) , m ∈ [ 0 , N − 1 ] y(n+m)=\text{x}^T(n+m)\text{w}(n),m \in [0,N-1] y(n+m)=xT(n+m)w(n),m∈[0,N−1],要保证至少有N个点的线性卷积和圆周卷积的结果相同,即 N 1 − N 2 + 1 ≥ N N_1-N_2+1 \ge N N1−N2+1≥N
-
由于 N 1 ≥ N 2 N_1 \ge N_2 N1≥N2,且滤波器阶数为N,因此 N 2 = N N_2=N N2=N,所以条件变为: N 1 ≥ 2 N − 1 N_1 \ge 2N-1 N1≥2N−1
-
为了方便FFT的计算,令 N 1 = 2 N N_1=2N N1=2N
-
根据下图,构造x(n)和w(n)

-
分别计算输入信号向量和滤波器向量的傅里叶变换
X ( k ) = d i a g { F [ x ( k N − N ) , . . . , x ( k N − 1 ) , x ( k N ) , . . . , x ( k N + N − 1 ) ] } W ( k ) = F [ w T ( k ) , 0 , . . . , 0 ] T Y ( k ) = X ( k ) W ( k ) \begin{aligned} X(k)&=diag\{ F[x(kN-N), ..., x(kN-1), x(kN), ..., x(kN+N-1)] \} \\ W(k)&=F[\text{w}^T(k), 0, ..., 0]^T \\ Y(k)&=X(k)W(k) \end{aligned} X(k)W(k)Y(k)=diag{F[x(kN−N),...,x(kN−1),x(kN),...,x(kN+N−1)]}=F[wT(k),0,...,0]T=X(k)W(k) -
每个Y(k)的长度为2N,输出序列y(k)的N点线性卷积等于Y(k)经过傅里叶逆变换的后N个点
y ( k ) = [ y ( k N ) , y ( k N + 1 ) , y ( k N ) , . . . , y ( k N + N − 1 ) ] = last N samples of F − 1 Y ( k ) \begin{aligned} y(k)&=[y(kN), y(kN+1), y(kN), ..., y(kN+N-1)] \\ &=\text{last N samples of }F^{-1}Y(k) \end{aligned} y(k)=[y(kN),y(kN+1),y(kN),...,y(kN+N−1)]=last N samples of F−1Y(k) -
y(k)的计算流程如下:
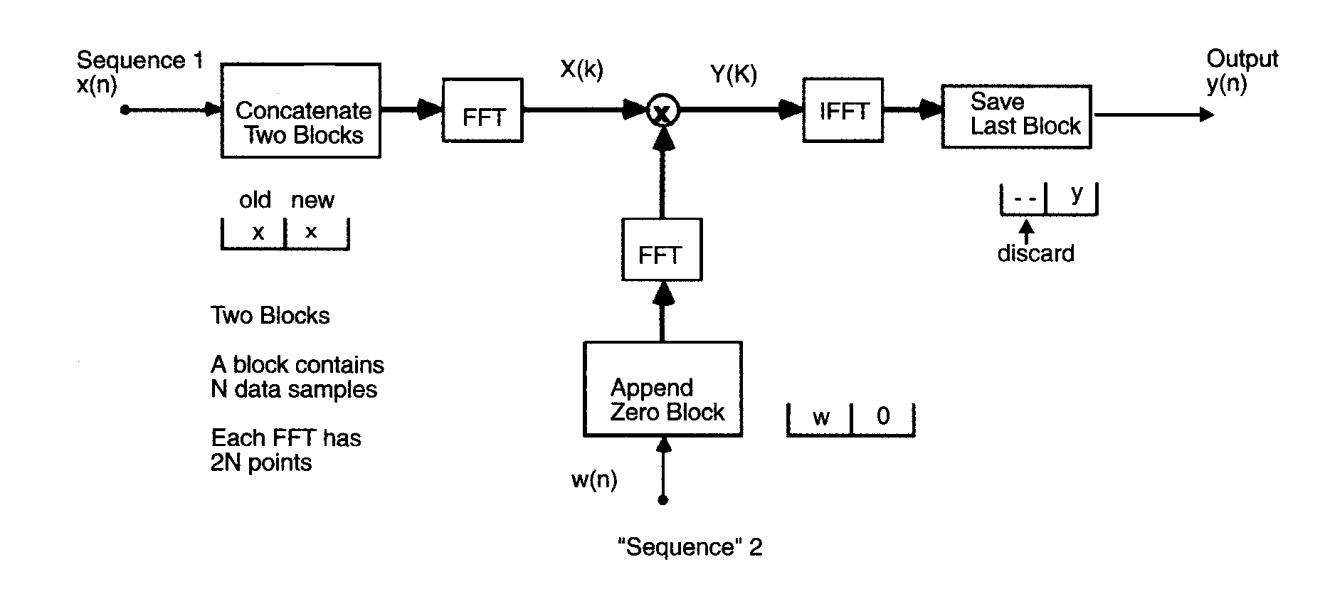
-
接下来计算N个点的瞬时梯度之和: ▽ ( k ) = − 2 ∑ m = 0 L − 1 x ( k L + m ) e ( k L + m ) \triangledown (k)=-2 \sum_{m=0}^{L-1} \text{x}(kL+m) e(kL+m) ▽(k)=−2∑m=0L−1x(kL+m)e(kL+m)
-
对于线性相关运算,仍然是变换到频域,计算输入信号的共轭谱与误差序列的乘积
-
X(k)在上面已求得,接下来将误差序列 e ( k ) = [ e ( k N ) , e ( k N + 1 ) , . . . , e ( k N + N − 1 ) ] e(k)=[e(kN), e(kN+1), ..., e(kN+N-1)] e(k)=[e(kN),e(kN+1),...,e(kN+N−1)]也扩展到2N的长度
-
注意:计算卷积时,在w(n)的后面补N个0,计算相关时,在e(n)的前面补N个0
-
误差序列的傅里叶变换 E ( k ) = F [ 0 , 0 , . . . , 0 , e T ( k ) ] T E(k)=F[0, 0, ..., 0, e^T(k)]^T E(k)=F[0,0,...,0,eT(k)]T
-
瞬时梯度的傅里叶变换 ▽ ( k ) = X H ( k ) E ( k ) \bigtriangledown (k)=X^H(k)E(k) ▽(k)=XH(k)E(k)
-
每个 ▽ ( k ) \bigtriangledown (k) ▽(k)的长度为2N,瞬时梯度之和的N点线性相关等于 ▽ ( k ) \bigtriangledown (k) ▽(k)经过傅里叶逆变换的前N个点
▽ ⃗ ( k ) = [ ▽ ( k N ) , ▽ ( k N + 1 ) , ▽ ( k N ) , . . . , ▽ ( k N + N − 1 ) ] = first N samples of F − 1 ▽ ( k ) \begin{aligned} \vec{\triangledown}(k)&=[\triangledown(kN), \triangledown(kN+1), \triangledown(kN), ..., \triangledown(kN+N-1)] \\ &=\text{first N samples of }F^{-1}\bigtriangledown(k) \end{aligned} ▽(k)=[▽(kN),▽(kN+1),▽(kN),...,▽(kN+N−1)]=first N samples of F−1▽(k)
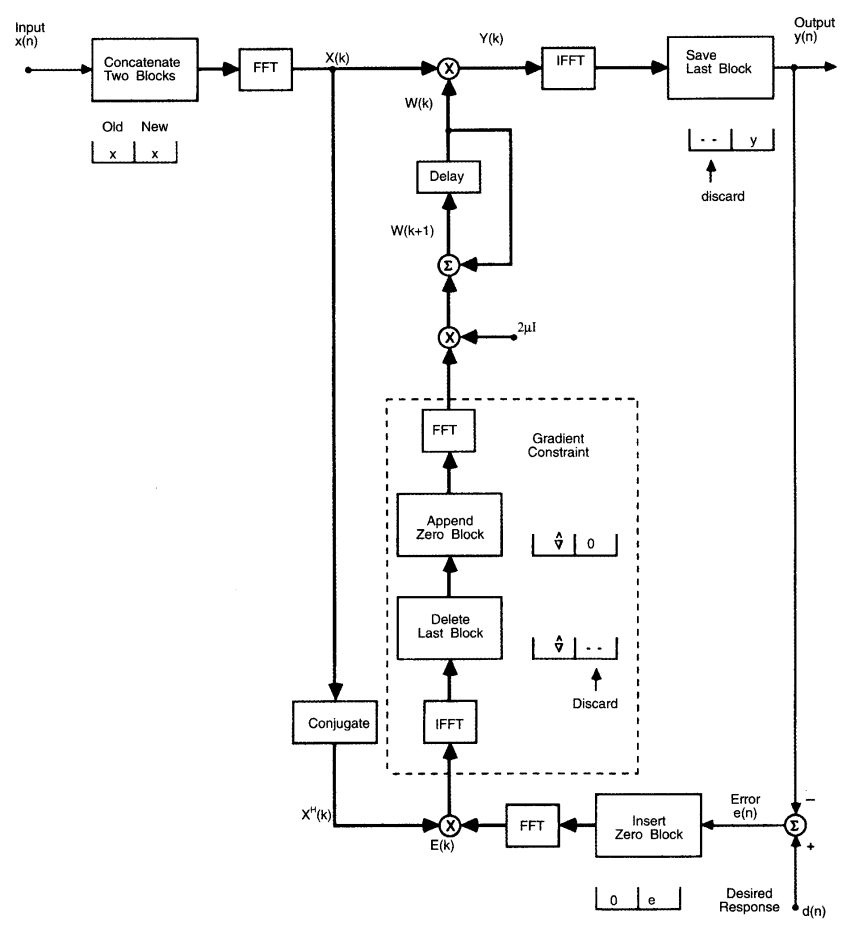
Frequency-Domain Adaptive Filter(FDAF)
- 滤波器系数的更新也可以在频域完成 W ( k + 1 ) = W ( k ) + 2 μ F [ ▽ ⃗ T ( k ) , 0 , . . . , 0 ] T W(k+1)=W(k)+2\mu F[\vec{\triangledown}^T(k), 0, ..., 0]^T W(k+1)=W(k)+2μF[▽T(k),0,...,0]T
- 注意
- 滤波器系数直接在频域更新,所以需要将梯度向量再次变换到频域
- 由于滤波器系数在后面补N个0,所以梯度向量也需要在后面补N个0
- FDAF的整体框架如下: