目录
1143.最长公共子序列
思路
1、确定dp数组
2、确定递推公式
3、dp数组初始化
4、遍历顺序
5、推导dp数组
最长公共子序列
1035.不相交的线
思路
不相交的线
53. 最大子序和
思路
最大子序列
动态规划
贪心算法
1143.最长公共子序列
题目链接:力扣
思路
不知道为什么,子序列问题的动态规划感觉比 背包问题 和 买卖股票问题 这两类题目难理解很多,比较了以下,可能是因为之前的数组,横列数列代表的都是不同的东西,而序列问题横列和数列代表的都是字符串本身,可能是这个原因吧,还不太清楚
可以看一下这个视频的图表推导:对照着代码更容易理解:最长公共子序列
1、确定dp数组
dp[i][j]:长度为[0, i]的字符串text1与长度为[0, j]的字符串text2的最长公共子序列为dp[i][j]
2、确定递推公式
两种情况:
- text1[ i ] 与 text2[ j ]相同
- 那就是找到了一个公共元素,所以:dp[ i ][ j ] = dp[i - 1][j - 1] + 1;
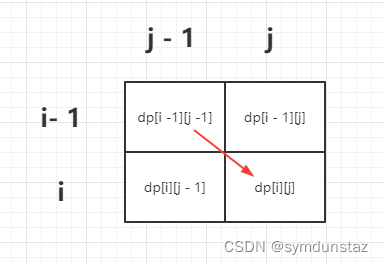
- 那就是找到了一个公共元素,所以:dp[ i ][ j ] = dp[i - 1][j - 1] + 1;
- text1[ i ] 与 text2[ j ]不相同
- 那就要看看长度为[0, i - 1]的text1与长度为[0 , i]的text2 的最长公共子序列
与长度为[0, i ]的text1与长度为[0 , i - 1]的text2 的最长公共子序列
这两个哪个最大,取最大的
所以:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
- 那就要看看长度为[0, i - 1]的text1与长度为[0 , i]的text2 的最长公共子序列
- 最终的代码就为
if (text1[i - 1] == text2[j - 1]) { dp[i][j] = dp[i - 1][j - 1] + 1; } else { dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); }
3、dp数组初始化
dp[i][0] 表示:长度为[0, i ]的text1 与 空串的最长公共子序列,那肯定是 0 ,所以dp[i][0] = 0;
同理:dp[0][j] = 0
其他的会根据上面的一列一行,计算覆盖,所以赋值什么都可以的,所以统一默认为0 就行

4、遍历顺序
从前向后遍历
5、推导dp数组

dp数组的 行和列 是比两个字符串的长度多1的,这是一个面对代码不太好理解的点
所以在遍历字符串的时候都是从1开始,求的第一个其实就是 dp[1][1] ,但是此时是根据初始化的那部分来求的,此时是字符串以下标的 0 和 0 结尾的字符串,但是是dp数组的[1][1]

最长公共子序列
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
// 创建dp数组
int[][] dp = new int[text1.length() + 1][text2.length() + 1];
// 初始化dp数组
// 默认就是初始化
// 推导dp数组
for (int i = 1; i <= text1.length(); i++) {
char chi = text1.charAt(i - 1);
for (int j = 1; j <= text2.length(); j++) {
char chj = text2.charAt(j - 1);
if (chi == chj) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j]);
}
}
}
return dp[text1.length()][text2.length()];
}
}1035.不相交的线
题目链接:力扣
思路
这道题目是求不相交的线,其实就是求两个数组的最长公共子序列,这样就跟上一道题目一样了,一模一样的代码,就是把字符串换成了数组
不相交的线
class Solution {
public int maxUncrossedLines(int[] nums1, int[] nums2) {
// 创建dp数组
int[][] dp = new int[nums1.length + 1][nums2.length + 1];
// 初始化dp数组
// 推导dp数组
for (int i = 1; i <= nums1.length; i++) {
for (int j = 1; j <= nums2.length; j++) {
if (nums1[i-1] == nums2[j-1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j]);
}
}
}
return dp[nums1.length][nums2.length];
}
}53. 最大子序和
题目链接:力扣
思路
看起来简单,自己写了一下,还是有不少细节的,只要是初始化和result的赋值 ,如果摸不准就在推导完dp数组后在选取最大值
1、确定dp数组的含义
dp[i]:包括下标i之前的最大连续子序列和为dp[i]
2、确定递推公式
做过贪心算法的方法就很容易理解,有两种情况
- dp[i - 1] + nums[i],即:nums[i]加入当前连续子序列和
- nums[i],即:从头开始计算当前连续子序列和
3、初始化
从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态,dp[0]就是递推公式的基础。
dp[0]应为nums[0]即dp[0] = nums[0]
4、遍历顺序
从前向后进行遍历
最大子序列
动态规划
// 在推导dp数组的过程中获取最大值
class Solution {
public int maxSubArray(int[] nums) {
// 创建dp数组
int[] dp = new int[nums.length];
// 初始化dp数组
dp[0] = nums[0];
// 推导dp数组
// 获取结果
int result = nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(nums[i],dp[i - 1] + nums[i]);
if (dp[i] > result) {
result = dp[i];
}
}
return result;
}
}
// 推导完dp数组后再获取最大值
class Solution {
public int maxSubArray(int[] nums) {
// 创建dp数组
int[] dp = new int[nums.length];
// 初始化dp数组
dp[0] = nums[0];
// 推导dp数组
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(nums[i],dp[i - 1] + nums[i]);
}
// 获取结果
int result = Integer.MIN_VALUE;
for (int num : dp) {
result = num > result ? num : result;
}
return result;
}
}贪心算法
class Solution {
public int maxSubArray(int[] nums) {
int result = Integer.MIN_VALUE;
int count = 0;
for (int i = 0; i < nums.length; i++) {
count += nums[i];
if (count > result) {
result = count;
}
if (count < 0) {
count = 0;
}
}
return result;
}
}