倒三角数学符号为▼ 。英文为Nabla，中文读音为奈不拉，同时也可以读作“Del” 。这是场论中的符号，是矢量微分算符。 

一张图读懂导数与weifen

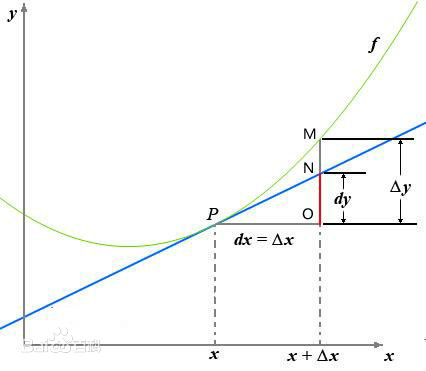
这是高数中的一张经典图，如果忘记了导数微分的概念，基本看着这张图就能全部想起来

反映的是函数y=f(x)在某一点处沿x轴正方向的变化率。再强调一遍，是函数f(x)在x轴上某一点处沿着x轴正方向的变化率/变化趋势。直观地看，也就是在x轴上某一点处，如果f’(x)>0，说明f(x)的函数值在x点沿x轴正方向是趋于增加的；如果f’(x)<0，说明f(x)的函数值在x点沿x轴正方向是趋于减少的。

　这里补充上图中的Δy、dy等符号的意义及关系如下：
　Δx：x的变化量；
　dx：x的变化量Δx趋于0时，则记作微元dx；
　Δy：Δy=f(x0+Δx)-f(x0)，是函数的增量；
　dy：dy=f’(x0)dx，是切线的增量；
　当Δx→0时，dy与Δy都是无穷小，dy是Δy的主部，即Δy=dy+o(Δx).

导数和偏导数
　偏导数的定义如下：
　 

　可以看到，导数与偏导数本质是一致的，都是当自变量的变化量趋于0时，函数值的变化量与自变量变化量比值的极限。直观地说，偏导数也就是函数在某一点上沿坐标轴正方向的的变化率。
　区别在于：
　导数，指的是一元函数中，函数y=f(x)在某一点处沿x轴正方向的变化率；
　偏导数，指的是多元函数中，函数y=f(x1,x2,…,xn)在某一点处沿某一坐标轴（x1,x2,…,xn）正方向的变化率。
　

导数和偏导数的区别

一、定义不同

导数，是对含有一个自变量的函数进行求导。

偏导数，是对含有两个自变量的函数中的一个自变量求导。

一元函数，一个y对应一个x，导数只有一个。二元函数，一个z对应一个x和一个y，那就有两个导数了，一个是z对x的导数，一个是z对y的导数，称之为偏导。

二、几何意义不同

函数y=f（x）在x0点的导数f'（x0）的几何意义：表示函数曲线在点P0（x0,f（x0））处的切线的斜率（导数的几何意义是该函数曲线在这一点上的切线斜率）。

偏导数 f'x(x0,y0) 表示固定面上一点对 x 轴的切线斜率；偏导数 f'y(x0,y0) 表示固定面上一点对 y 轴的切线斜率。

高阶偏导数：如果二元函数 z=f(x,y) 的偏导数 f'x(x,y) 与 f'y(x,y) 仍然可导，那么这两个偏导函数的偏导数称为 z=f(x,y) 的二阶偏导数。二元函数的二阶偏导数有四个：f"xx，f"xy，f"yx，f"yy。

梯度的提出只为回答一个问题：
　函数在变量空间的某一点处，沿着哪一个方向有最大的变化率？
　梯度定义如下：
　函数在某一点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。
　这里注意三点：
　1）梯度是一个向量，即有方向有大小；
　2）梯度的方向是最大方向导数的方向；
　3）梯度的值是最大方向导数的值。
　

导数与向量
　提问：导数与偏导数与方向导数是向量么？
　向量的定义是有方向（direction）有大小（magnitude）的量。
　从前面的定义可以这样看出，偏导数和方向导数表达的是函数在某一点沿某一方向的变化率，也是具有方向和大小的。因此从这个角度来理解，我们也可以把偏导数和方向导数看作是一个向量，向量的方向就是变化率的方向，向量的模，就是变化率的大小。
　那么沿着这样一种思路，就可以如下理解梯度：
　梯度即函数在某一点最大的方向导数，函数沿梯度方向函数有最大的变化率。
　
　

梯度下降法
　既然在变量空间的某一点处，函数沿梯度方向具有最大的变化率，那么在优化目标函数的时候，自然是沿着负梯度方向去减小函数值，以此达到我们的优化目标。
　如何沿着负梯度方向减小函数值呢？既然梯度是偏导数的集合，如下：
　 

　同时梯度和偏导数都是向量，那么参考向量运算法则，我们在每个变量轴上减小对应变量值即可，梯度下降法可以描述如下：
　 

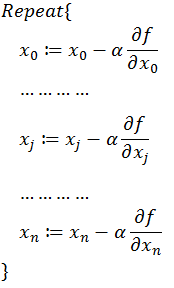
　以上就是梯度下降法的由来，大部分的机器学习任务，都可以利用Gradient Descent来进行优化。
--------------------- 

总结：

1.导数定义： 导数代表了在自变量变化趋于无穷小的时候，函数值的变化与自变量的变化的比值。几何意义是这个点的切线。物理意义是该时刻的（瞬时）变化率。

注意：在一元函数中，只有一个自变量变动，也就是说只存在一个方向的变化率，这也就是为什么一元函数没有偏导数的原因。
（derivative）

2.偏导数： 既然谈到偏导数，那就至少涉及到两个自变量。以两个自变量为例，z=f（x,y），从导数到偏导数，也就是从曲线来到了曲面。曲线上的一点，其切线只有一条。但是曲面上的一点，切线有无数条。而偏导数就是指多元函数沿着坐标轴的变化率。
注意：直观地说，偏导数也就是函数在某一点上沿坐标轴正方向的的变化率。
（partial derivative）

3.方向导数: 在某点沿着某个向量方向上的方向导数，描绘了该点附近沿着该向量方向变动时的瞬时变化率。这个向量方向可以是任一方向。

方向导数的物理意义表示函数在某点沿着某一特定方向上的变化率。
注意：导数、偏导数和方向导数表达的是函数在某一点沿某一方向的变化率，也是具有方向和大小的。
（directional derivative）

4.梯度: 函数在给定点处沿不同的方向，其方向导数一般是不相同的。那么沿着哪一个方向其方向导数最大，其最大值为多少，这是我们所关心的，为此引进一个很重要的概念: 梯度。

5.梯度下降
在机器学习中往往是最小化一个目标函数 L(Θ)，理解了上面的内容，便很容易理解在梯度下降法中常见的参数更新公式：

Θ = Θ − γ ∂ L ∂ Θ
通过算出目标函数的梯度（算出对于所有参数的偏导数）并在其反方向更新完参数 Θ ，在此过程完成后也便是达到了函数值减少最快的效果，那么在经过迭代以后目标函数即可很快地到达一个极小值。

6.In summary:
概念 　　物理意义
导数 　　函数在该点的瞬时变化率
偏导数 　函数在坐标轴方向上的变化率
方向导数 函数在某点沿某个特定方向的变化率
梯度 　　函数在该点沿所有方向变化率最大的那个方向