根据目标个数,分为单目标规划,以及多目标规划。多目标的规划是去找折中的解集合,既pareto最优解集合。对优化目标超过3个以上的,称之为超多目标优化问题。
- 帕累托改进描述的就是在没有人变得不好的前提下让有些人更好的过程。帕累托改进的终极形态是帕累托最优。改进是过程,最优是结果,帕累托最优就是指再没有改进余地的状态。
- 在达到帕累托最优后,如果还要进一步改进,就不得不牺牲一部分人利益来换取集体更大的利益,这个过程叫作卡尔多-希克斯改进。
一、基础概念
- 可行解和可行域:就是满足约束的那些x包起来的区域。
- pareto支配:(解A支配解B)解A每个目标都不比B差且至少有一个好过B
- pareto最优解:可行域中没有别的解的可以支配它
- pareto最优解集:决策空间中的pareto最优解构成的集合,称为PS
- pareto最优前沿:PS映射到目标空间张成的面,PF
1:解A优于解B(解A强帕累托支配解B)
假设现在有两个目标函数,解A对应的目标函数值都比解B对应的目标函数值好,则称解A比解B优越,也可以叫做解A强帕累托支配解B,举个例子,就很容易懂了
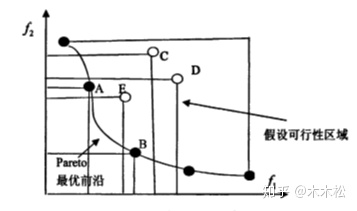
下图中代表的是两个目标的的解的情况,横纵坐标表示两个目标函数值,E点表示的解所对应的两个目标函数值都小于C,D两个点表示的解所对应的两个目标函数值,所以解E优于解C,D.
2:解A无差别于解B(解A帕累托非支配解B)
同样假设两个目标函数,解A对应的一个目标函数值优于解B对应的一个目标函数值,但是解A对应的另一个目标函数值要差于解B对应的一个目标函数值,则称解A无差别于解B,也叫作解A能帕累托支配解B,举个例子,还是上面的图,点C和点D就是这种情况,C点在第一个目标函数的值比D小,在第二个函数的值比D大。
3:帕累托最优前沿
如下图所示,更好的理解一下帕累托最优解,实心点表示的解都是帕累托最优解,所有的帕累托最优解构成帕累托最优解集,这些解经目标函数映射构成了该问题的Pareto最优前沿或Pareto前沿面,说人话,即帕累托最优解对应的目标函数值就是帕累托最优前沿。
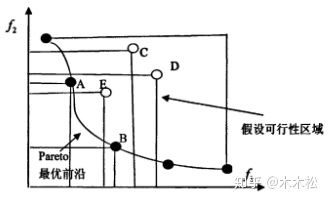
对于两个目标的问题,其Pareto最优前沿通常是条线。而对于多个目标,其Pareto最优前沿通常是一个超曲面。
二、帕累托改进与帕累托最优
说到帕累托最优,不得不先提一下帕累托改进,两个就像孪生兄弟,总是成对出现。
帕累托改进
那什么是帕累托改进呢?用一句话概括,就是在没有人变得不好的前提下让有些人更好。
举个例子,假设A和B两人手上各有一只橘子,A只想用橘子皮泡水喝,B只想吃它的果肉,所以对于A来说,橘子皮是有用的,果肉没用,对于B来说,果肉是有用的,橘子皮没用。于是他们商量后决定把自己没用的那部分相互交换,这样A就能得到两份橘子皮,B能得到两份果肉,两人都比之前多了一倍。
这个案例描述的就是典型的帕累托改进,对照定义看一下,是不是满足“在没有人变得不好的前提下让有些人更好”呢?完全满足。
这个例子乍一看是不是有点像两个国家在利用各自优势进行贸易互换?没错,基于比较优势理论的全球分工合作模式就是一种帕累托改进。
理解了帕累托改进就不难理解帕累托最优。帕累托最优就是指再也找不到任何帕累托改进的余地的状态。
如上所述,A和B交换橘子皮和果肉的过程就是持续的帕累托改进,每交换一片果肉和一片橘子皮都是一次帕累托改进,直到交换完整只橘子为止,而这个完成的状态就叫帕累托最优,此时你不可能再得到更多的橘子皮和果肉了。
三、进化版:卡尔多-希克斯改进
帕累托改进描述的是一种理想状态,在帕累托改进中没有任何人的利益会受损,每个人至少要好于或等于当前状态,从而使整体的福利得到增加。顺带提一嘴,经济学里的福利指的是物质或精神的满足。
但在现实中这种情况过于理想化了,不妨设想一种更常见的场景,即对于集体来讲,部分受益、部分受损,但只要受益部分大于受损部分,那么集体的总福利也可以得到提升,此时受益者也可以给予受损者一定补偿以使其免遭损失。这个过程就是卡尔多-希克斯改进。
我们通过一个具体的例子来体会帕累托改进和卡尔多-希克斯改进的区别,假设甲乙两人打算共同投资一个项目,当前有A和B两个项目。
对于A项目,甲能盈利100万,乙能盈利200万;对于B项目,甲能盈利200万,乙能盈利150万。如果按照帕累托改进的思想来挑项目,则A和B都选不上,因为帕累托要求任何一方的利益都不会受损,但是选A项目甲的利益会受损(甲少赚100万),选B项目乙的利益会受损(乙少赚50万)。
如果按照卡尔多-希克斯改进的思想来挑项目,那么应该选B项目。因为B相比A,甲能多赚100万,乙亏损50万,只要甲能拿出50万补贴乙,那么在乙不受损的情况下,甲还能多赚50万,整体的福利更高。
超多目标演化算法综述——基本概念和研究背景 - 知乎
如何通俗地解释「帕累托最优」(Pareto optimum)? - 知乎