目录

1.邻接表相关知识补充

 2. 图的邻接存储表示

3.测试输入与输出样例

4.代码实现

4.1 创建无向图邻接表

4.2 输入无向图的邻接表

---

1.邻接表相关知识补充

定义：

对于图中每个顶点 vi，把所有邻接于 vi的顶点（对有向图是将从vi出发的弧的弧头顶点链接在一起）链接成一个带头结点的单链表，将所有头结点顺序存储在一个一维数组中。

示例：下面左图G2对应的邻接表如右边所示。

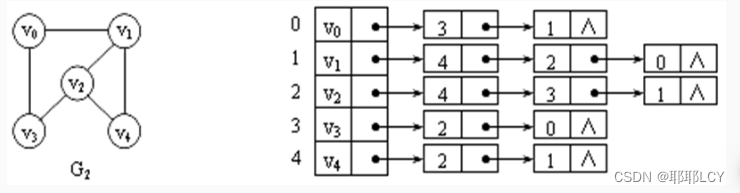
 2. 图的邻接存储表示

#define MAXVEX 20 /*最大顶点数*/
typedef enum{DG,DN,UDG,UDN} GraphKind; /*有向图，有向网，无向图，无向网*/
typedef struct ENode /*表结点类型*/
{
    int adjvex;
    struct ENode *nextarc;
    int weight;
}ENode;
typedef int VexType;
typedef struct VNode /*头结点类型*/
{
    VexType vex;
    ENode *firstarc;
}VNode, AdjList[MAXVEX]; /*邻接表类型定义*/
typedef struct
{
    AdjList vertices; /*用邻接表存储顶点集合及边集合*/
    int vexnum,edgenum;
    GraphKind kind;
}ALGraph; /*邻接表存储的图的类型定义*/

3.测试输入与输出样例

测试输入：

2 5 6

0 1 0 3 1 2 1 4 2 3 2 4

预期输出：

0->3->1

1->4->2->0

2->4->3->1

3->2->0 4->2->1

4.代码实现

这里主要写了两个函数，一个用于生成无向图的邻接表，一个用于输出其邻接表

4.1 创建无向图邻接表

void CreateUDG_ALG(ALGraph &g) /*构造无向图的邻接表*/
{
    int kind,dot,edges;
    scanf("%d %d %d",&kind,&dot,&edges);
    g.vexnum=dot;g.edgenum=edges;g.kind=(GraphKind)kind;
/*这里有关枚举的类型再赋值问题(g.kind)，枚举变量的再赋值不能直接是数字，如果是数字的话需要一个枚举/类型的强制转换*/
    VNode*pn=NULL;
    for(int i=0;i<dot;i++) //创建六个头结点
    {
        pn=new VNode;
        pn->vex=i;// VexType类型就是int类型
        pn->firstarc=NULL;//初始化置空
        g.vertices[i]=*pn;   //vertices数组类型是头结点类型
    }
    int x,y;
    ENode *en=NULL;ENode *tn=NULL; //都是边结点类型
    for(int j=0;j<edges;j++) //6个变，所以循环6次 开始创建邻接表
    {
        en= new ENode;    //边结点指针
        // scanf("%d",&x);  //第一个点
        // scanf("%d",&y);  //第二个点
        scanf("%d%d",&x,&y);  //也可以写在一起

        //将输入的信息添加到边结点上去，采用链表头插法的方式不停改变我们的指针
        en->adjvex=y;en->weight=0;en->nextarc=g.vertices[x].firstarc;
        g.vertices[x].firstarc=en;

        //下面这段代码也是一样的,采用链表头插法的方式        
        tn= new ENode;    //边结点指针
        tn->adjvex=x;tn->weight=0;tn->nextarc=g.vertices[y].firstarc;
        g.vertices[y].firstarc=tn;
    } 
}

4.2 输入无向图的邻接表

void PrintAdjList(ALGraph g) /*输出邻接表*/
{
    ENode *sn;//定义一个边结点指针，用于移动改变输出的边结点
    for(int i=0;i<g.vexnum;i++)
    {
        sn=g.vertices[i].firstarc;//初始化为每个顶点的第一条边的地址
        printf("%d",i);
        while(sn!=NULL)//循环输出我们的每个顶点的边结点信息
        {
            printf("->%d",sn->adjvex);

//每输出完一个边结点就移动至下一个边结点，直到最后一个边结点为止，也就是指针为空的时候
            sn=sn->nextarc;
        }
        printf("\n");//完成一个顶点的全部边结点输出后，换行
    }
}

整体就是采用循环的方式，头插法创建我们的无向图的邻接表，关键在于其中我们指针的移动。