文章目录
- 总结
- 大纲要求
- 算法概念
- 举个例子:量水问题
- 算法描述
- 算法的时间复杂度

总结
本系列为C++算法学习系列,会介绍 算法概念与描述,入门算法,基础算法,数值处理算法,排序算法,搜索算法,图论算法, 动态规划等相关内容。本文为C+算法概念与描述部分。
大纲要求
【 1 】算法概念
【 2 】算法描述:自然语言描述、流程图描述、 伪代码描述
算法概念
信息学奥赛算法是指用计算机解决问题的方法和技巧。其核心在于算法的设计和优化,包括时间复杂度和空间复杂度等方面的优化。下面是一些常见的算法概念介绍:
-
排序算法:将一组数据按照指定的规则进行排序的算法,包括冒泡排序、快速排序、归并排序等。
-
搜索算法:通过遍历某个数据集合来查找特定元素的算法,包括二分查找、深度优先搜索、广度优先搜索等。
-
图论算法:用于解决图论相关问题的算法,包括最短路径算法、最小生成树算法、拓扑排序等。
-
动态规划算法:将一个问题分解成一个个子问题来求解的算法,包括最大子序列和、最长公共子序列等。
-
贪心算法:在每一步选择中都采取在当前状态下最优的选择,从而希望导致结果是全局最优的算法,包括背包问题等。
-
分治算法:将问题分解成多个小问题来求解的算法,包括快速排序、归并排序等。
-
字符串算法:用于解决字符串相关问题的算法,包括KMP算法、Trie树等。
举个例子:量水问题
假设有两只没有刻度的桶A和B,A可以装7升水,B可以装5升水,问:如何通过A和B互相倒腾得到六升水。
解:
将A装满(0升变7升)
将A的水倒向B,(A从7升剩2升,B变5升)
将B倒掉,
将A(2升b变0)倒向B(0变2升)
将A装满水
将A倒向B(此时A从7升变4升,B从2升变5升)
将B倒掉,
将A(4升)倒向B(从0升变4升)
将A装满水
将A再倒向B(从4升变5升,A此时剩余6升。
简化步骤:
将下面(2,3,4,5)重复两次
2、将A装满
3、将A的水倒向B
4、将B倒掉
5、将A倒向B
6、将A装满水
7、将A再倒向B
算法简单来说就是准确描述的“操作步骤”。
什么是计算机算法 —— 从特殊到一般的追求。
上面的例子我们给定的是具体的值,但是计算机算法是要追求一般的规律。
我们可以理解为数学公式,它不是具体的值,但解释了一般规律。
算法描述
算法描述:自然语言描述、流程图描述、 伪代码描述
**自然语言描述:**通过自然语言来描述算法的步骤和操作。例如,冒泡排序算法可以用如下自然语言描述:从数组的第一个元素开始,依次比较相邻的两个元素,如果前一个元素大于后一个元素,则交换它们的位置,直到将最大的元素移动到数组的最后一个位置。重复上述操作,直到所有元素都排好序为止。
初始化变量 i 和 j 为 0,表示当前需要比较的元素下标。
在数组 A 中比较 A[i] 和 A[j] 两个元素,如果 A[i] 大于 A[j],则交换它们的位置。
将 j 增加 1,如果 j < n,则回到步骤 2;否则,将 i 增加 1,将 j 重置为 i,如果 i < n-1,则回到步骤 2。
当 i >= n-1 时,排序结束。
**流程图描述:**通过图形化方式来表示算法的步骤和操作。例如,下图是一个简单的冒泡排序算法的流程图描述:
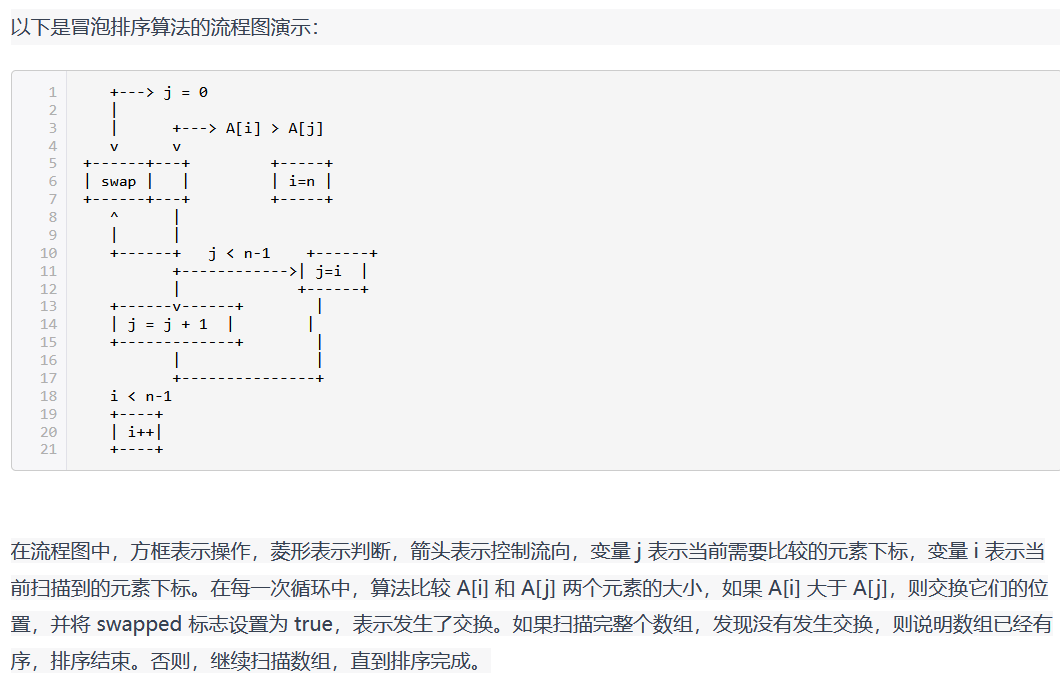
**伪代码描述:**通过一种类似编程语言的语法来描述算法的步骤和操作。伪代码通常比自然语言描述更具体和精确。例如,下面是一个用伪代码描述的冒泡排序算法:
procedure bubbleSort(A : list of sortable items)
n = length(A)
repeat
swapped = false
for i = 1 to n-1 do
if A[i] > A[i+1] then
swap(A[i], A[i+1])
swapped = true
end if
end for
n = n - 1
until not swapped
end procedure
假设有两只没有刻度的桶A和B,A可以装7升水,B可以装5升水,问:如何通过A和B互相倒腾得到六升水。
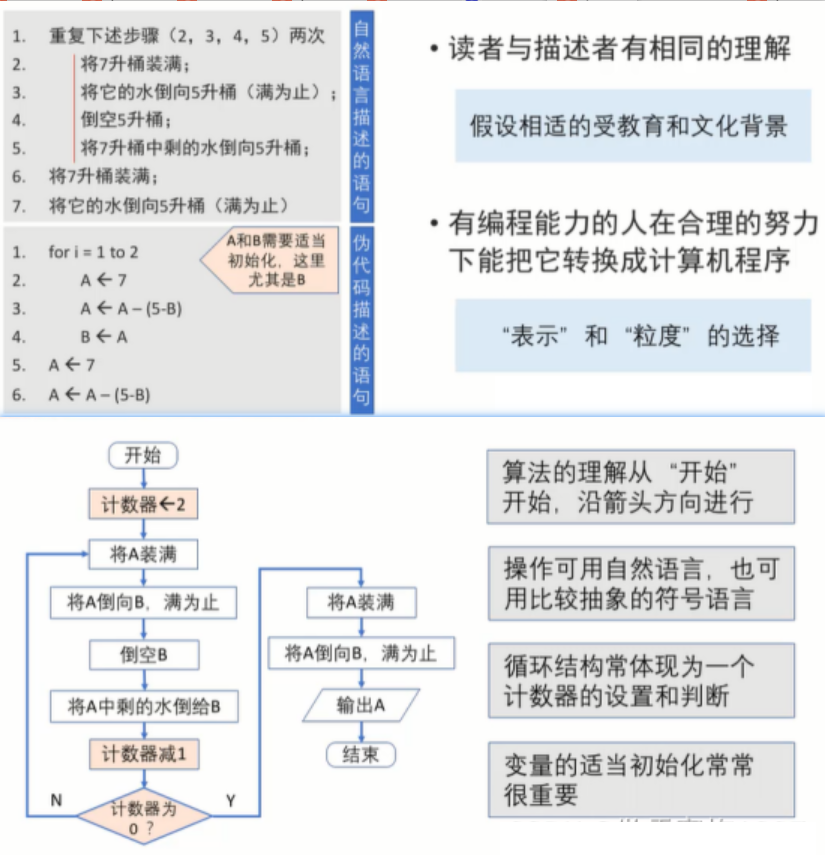
算法的时间复杂度
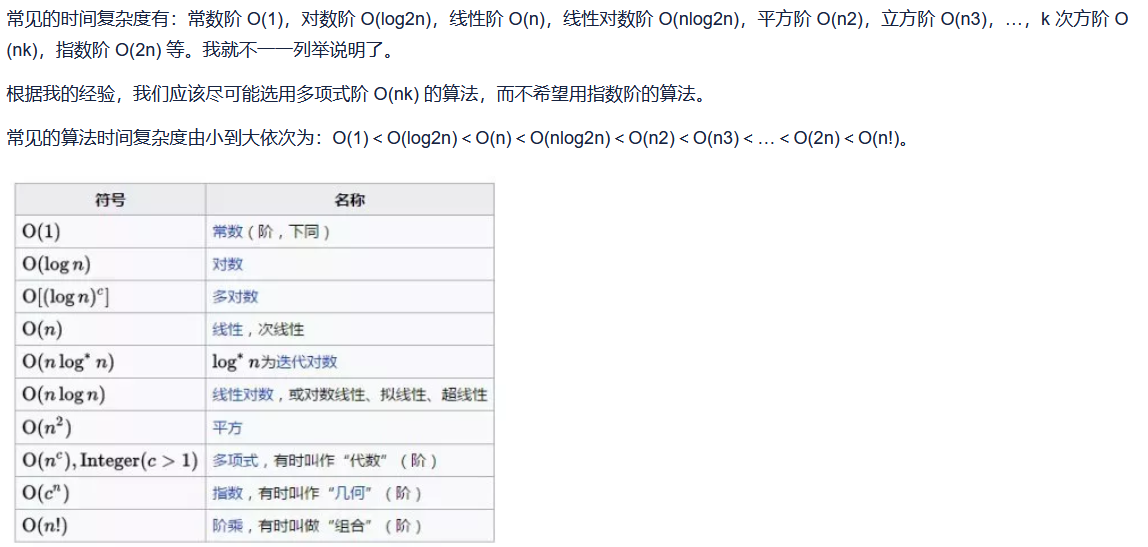
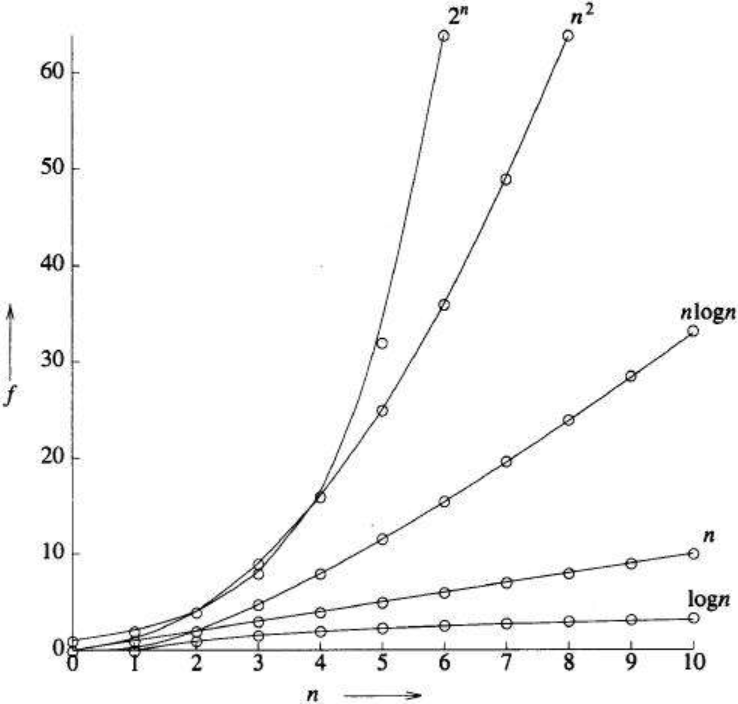
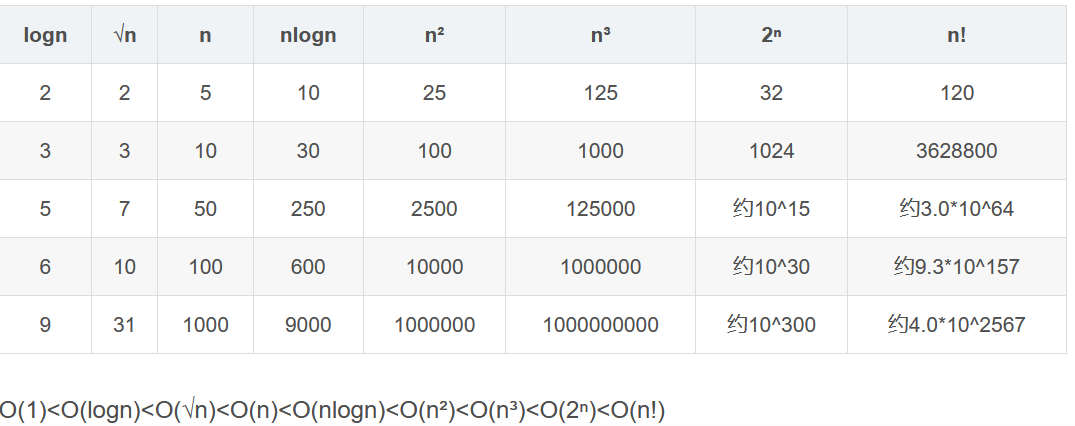
算法的时间复杂度是衡量算法运行时间效率的一种指标,通常用大O表示法来表达。它描述了算法在处理问题时所需的时间资源,即算法的时间复杂度越低,算法的执行效率越高。
时间复杂度通常表示为一个函数T(n),其中n表示输入规模。时间复杂度可以分为以下几类:
- 常数时间复杂度O(1),表示算法的执行时间与输入规模 n 无关,比如说访问数组中的一个元素。
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;
- 线性时间复杂度O(n),表示算法的执行时间与输入规模 n 成正比,比如说遍历一个数组。
for(i=1; i<=n; ++i)
{
j = i;
j++;
}
- 对数时间复杂度O(logn),表示算法的执行时间与输入规模 n 的对数成正比,通常出现在二分查找等算法中。
int i = 1;
while(i<n)
{
i = i * 2;
}
- 线性对数阶O(nlogN)
线性对数阶O(nlogN) 其实非常容易理解,将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是 n * O(logN),也就是了O(nlogN)。
for(m=1; m<n; m++)
{
i = 1;
while(i<n)
{
i = i * 2;
}
}
- 平方时间复杂度O(n^2),表示算法的执行时间与输入规模 n 的平方成正比,通常出现在多重循环嵌套的算法中。
for(x=1; i<=n; x++)
{
for(i=1; i<=n; i++)
{
j = i;
j++;
}
}
- 指数时间复杂度O(2^n),表示算法的执行时间与输入规模 n 的指数成正比,通常只出现在具有递归性质的算法中。
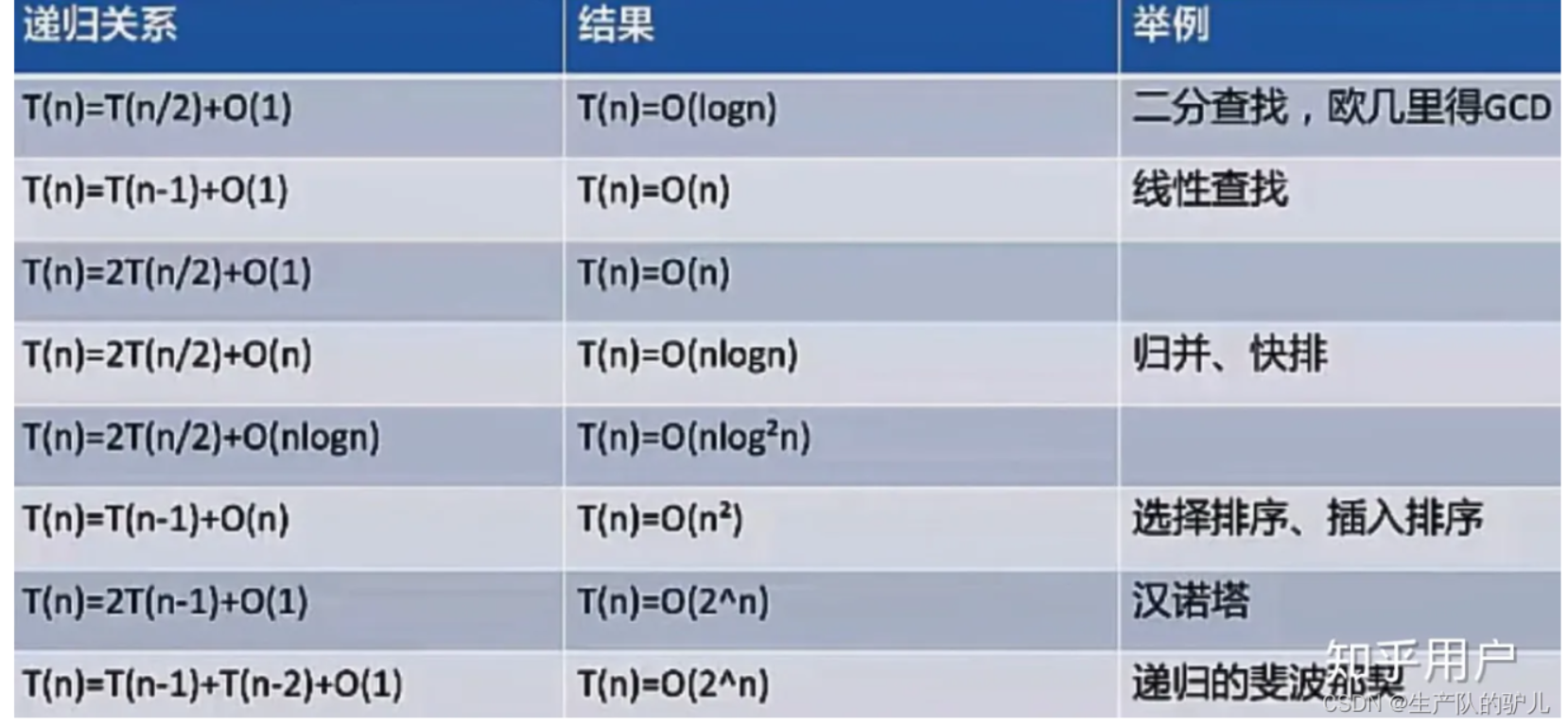
综上所述,算法的时间复杂度是评价算法效率的重要指标之一。在实际编程中,我们需要根据不同的需求选择不同的算法和数据结构,以提高程序的执行效率。算法的时间复杂度是衡量算法运行时间效率的一种指标,通常用大O表示法来表达。它描述了算法在处理问题时所需的时间资源,即算法的时间复杂度越低,算法的执行效率越高。