超平面中的任何点
x
x
x可以用一个法向量
w
w
w和超平面上的一个点
x
0
x_0
x0表示.

x
x
x可以用
w
w
w和
x
0
x_0
x0表示:
(
x
−
x
0
)
⋅
w
=
0
w
T
x
−
w
T
x
0
=
0
w
T
x
+
b
=
0
\begin{split} (x-x_0) \cdot w &=0 \\ w^Tx-w^Tx_0 &=0 \\ w^Tx+b &=0 \end{split}
(x−x0)⋅wwTx−wTx0wTx+b=0=0=0
其中
b
=
−
w
T
x
0
b=-w^Tx_0
b=−wTx0.
展开为
∑
i
=
1
k
w
i
∗
x
i
+
b
=
0
\sum_{i=1}^kw_i*x_i+b=0
∑i=1kwi∗xi+b=0,
x
x
x中的一个维度可以用其余的
k
−
1
k-1
k−1个维度表示,所以超平面是
k
−
1
k-1
k−1维的。
k维空间中的超平面的维度是多少?
news2026/2/12 8:03:59
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/584562.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
高压断路器工作运行要求是什么
1、断路器应在规定的技术参数范围内运行。
2、断路器必须配备可靠的操作电源和合闸电源。
3、送电应先合刀闸后合断路器;停电先断开断路器,检查确已断开后再拉刀闸。
4、110kV高压设备的巡视检查可由一人进行,但距带电体的距离应不小于1.5…
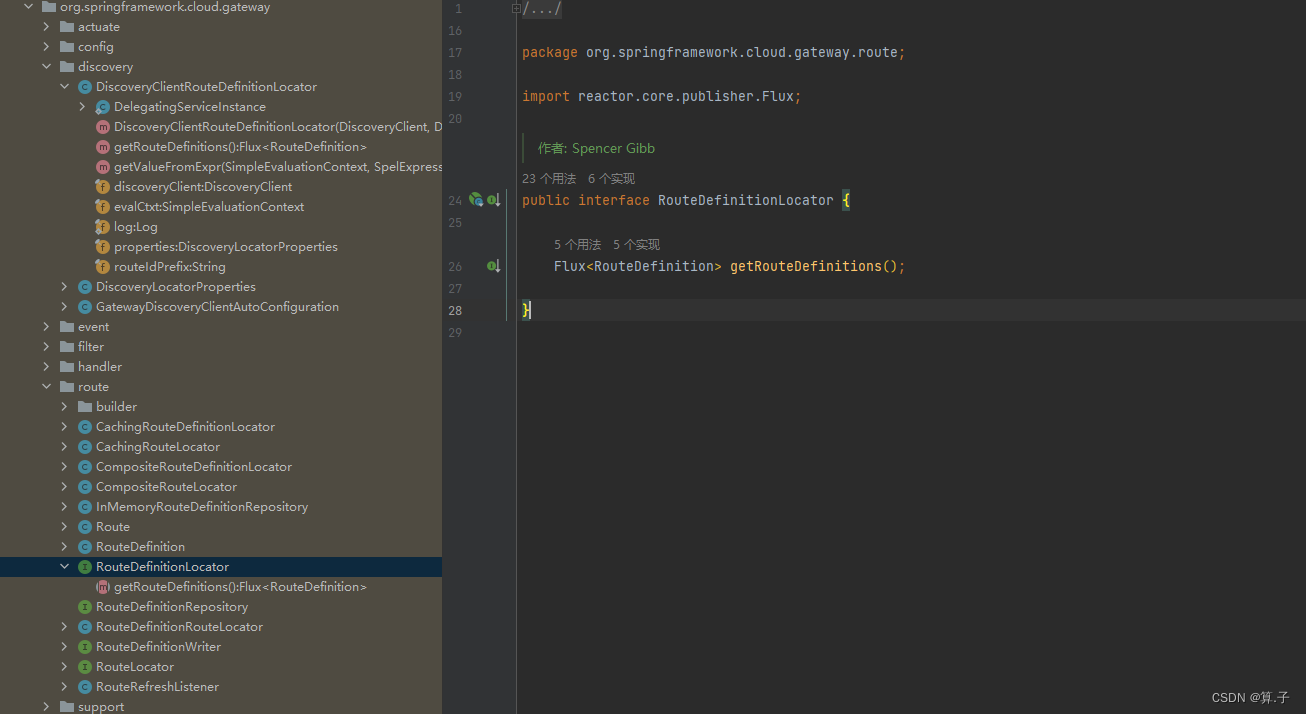
三分钟了解Spring Cloud Gateway路由转发之自动路由
文章目录 一、前言二、路由配置1. 静态路由2. 动态路由3. 自动路由 三、Spring Cloud Gateway 是如何实现动态路由工作原理源码解析路由转发原理路由转发源码解析 四 、问题核心DiscoveryClientRouteDefinitionLocator源码解析 五、总结 大家好,我是冰点,…
领导者指南:用四步空杯学习法避免你的成就成为累赘
好的领导者需要不断学习。而优秀的领导者更知道什么时候忘记过去,才能在未来取得成功。经营任何成功都存在学习曲线。但是,一旦你开始依赖过去的成就,或者陷入过时的思维和实践,不再起作用,你必须退后一步——空杯学习…
安捷伦E4440A(Agilent) e4440a 3HZ-26.5G频谱分析仪
Agilent E4440A、Keysight E4440A、HP E4440A频谱分析仪,3 Hz - 26.5 GHz(PSA 系列)
Agilent / Keysight PSA 系列 E4440A 高性能频谱分析仪提供强大的一键式测量、多功能功能集和前沿技术,可满足您的项目和需求。选项可供您选…
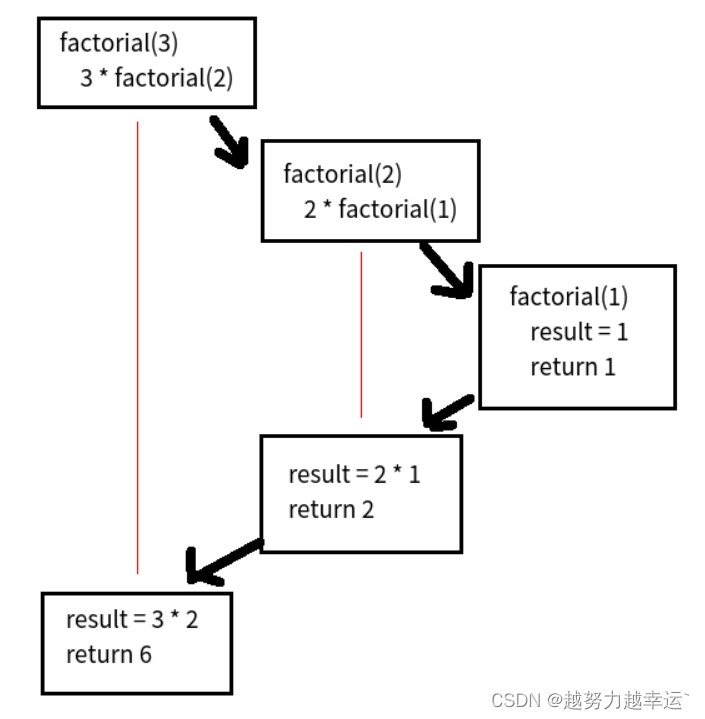
Python实战基础14-递归函数
1、什么是递归函数
如果一个函数在内部不调用其它的函数,而是自己本身的话,这个函数就递归函数。
遵循:
必须要有出口每次递归向出口靠近
# 1-10 打印数字
def test(i):if i 10:print(10)else:print(i)i 1test(i)
test(1)# 1-10 的累加…
海外网红营销ROI评估:出海品牌如何科学衡量投资回报?
随着全球化的不断推进,出海品牌越来越多地将目光投向海外市场,并利用海外网红的影响力进行营销。然而,对于出海品牌而言,如何科学衡量海外网红营销的投资回报率(ROI)却是一个关键的挑战。本文Nox聚星将和大…
Phaser笔记-精灵(sprite)的使用
如下: 使用逻辑如下:
①设置好physics;
②将资源添加到spritesheet;
③在physics中添加sprite;
④创建anims;
⑤播放anims; 完整代码如下:
import phaser;class PlayGame exte…
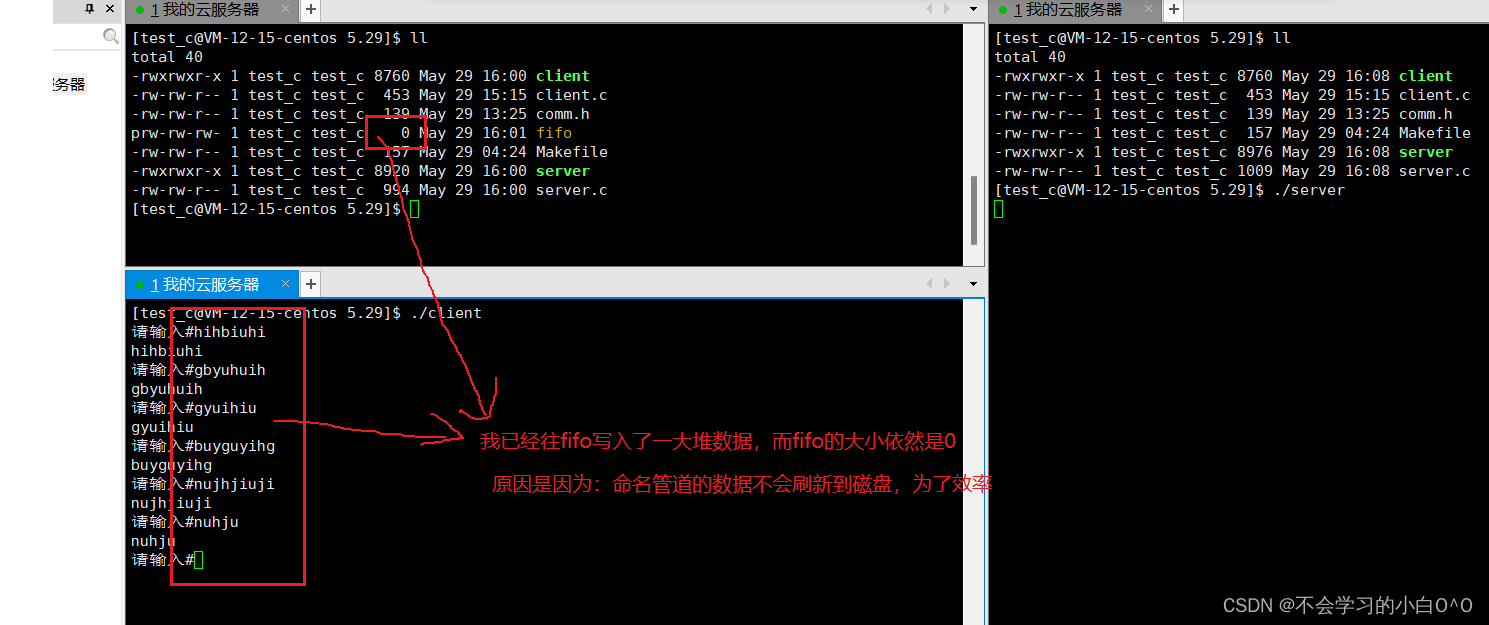
进程间通信(命名管道)
目录: 1.命名管道 2.创建命名管道
--------------------------------------------------------------------------------------------------------------------------------- 1.命名管道 1.管道的一个应用限制就是只能在具有共同祖先(具有亲缘关系&…
AI落地:高效学习指南
高效学习中有一个共识:学习最小可用知识,然后立马开始实践,做中学,不断获得反馈,不断在实践中改进。
现实生活中,如果我们想实现这种高效学习,基本上只能找一个老师1对1指导,费用贵…
[C语言][典例详解]打印杨辉三角(找规律简单实现)
目录 杨辉三角的相关知识
杨辉三角图: 杨辉三角的规律
在编程中实现
第一步 :我们先实现数字的打印,后面再加上空格构成三角形形状;
编辑
1.首先我们可以直观的看出三角形的两个斜边都是1;所以我们先打印斜边的…
S型平滑函数功能块(SCL+梯形图)
S型平滑和斜坡平滑函数从字面理解也知道大概用处了,这里就不再具体阐述。S型曲线在温控上面的应用请参看系列专栏,链接如下:
带平滑功能的斜坡函数(多段曲线控温纯S型曲线SCL源代码+完整算法分析)_s斜坡函数_RXXW_Dor的博客-CSDN博客PLC运动控制基础系列之梯形速度曲线,…
Java 集合和数组,集合和字符串,数组和字符串的相互转换
在 Java 中,可以通过以下方式实现集合、数组和字符串之间的相互转换。
一、集合和数组的相互转化
①、将集合转为数组:(toArray 方法)
List<String> list new ArrayList<>();
list.add("apple");
lis…
手写服务限流6种实现方式
服务限流,我有 6 种实现方式
ImportNew 2023-05-29 11:31 发表于上海
以下文章来源于码农参上 ,作者Dr Hydra 码农参上.
专注后端技术分享,有趣、深入、直接,与你聊聊技术。
今天来和大家聊聊服务的限流。 服务限流࿰…
2023 年 14 个最佳隐私和安全 Linux 发行版
随着数字时代的到来,隐私和安全成为了越来越重要的议题。对于那些关注隐私和安全的用户来说,选择一款专注于保护用户数据和系统安全的Linux发行版是至关重要的。在本文中,我们将介绍2023年14个最佳的隐私和安全Linux发行版,这些发…
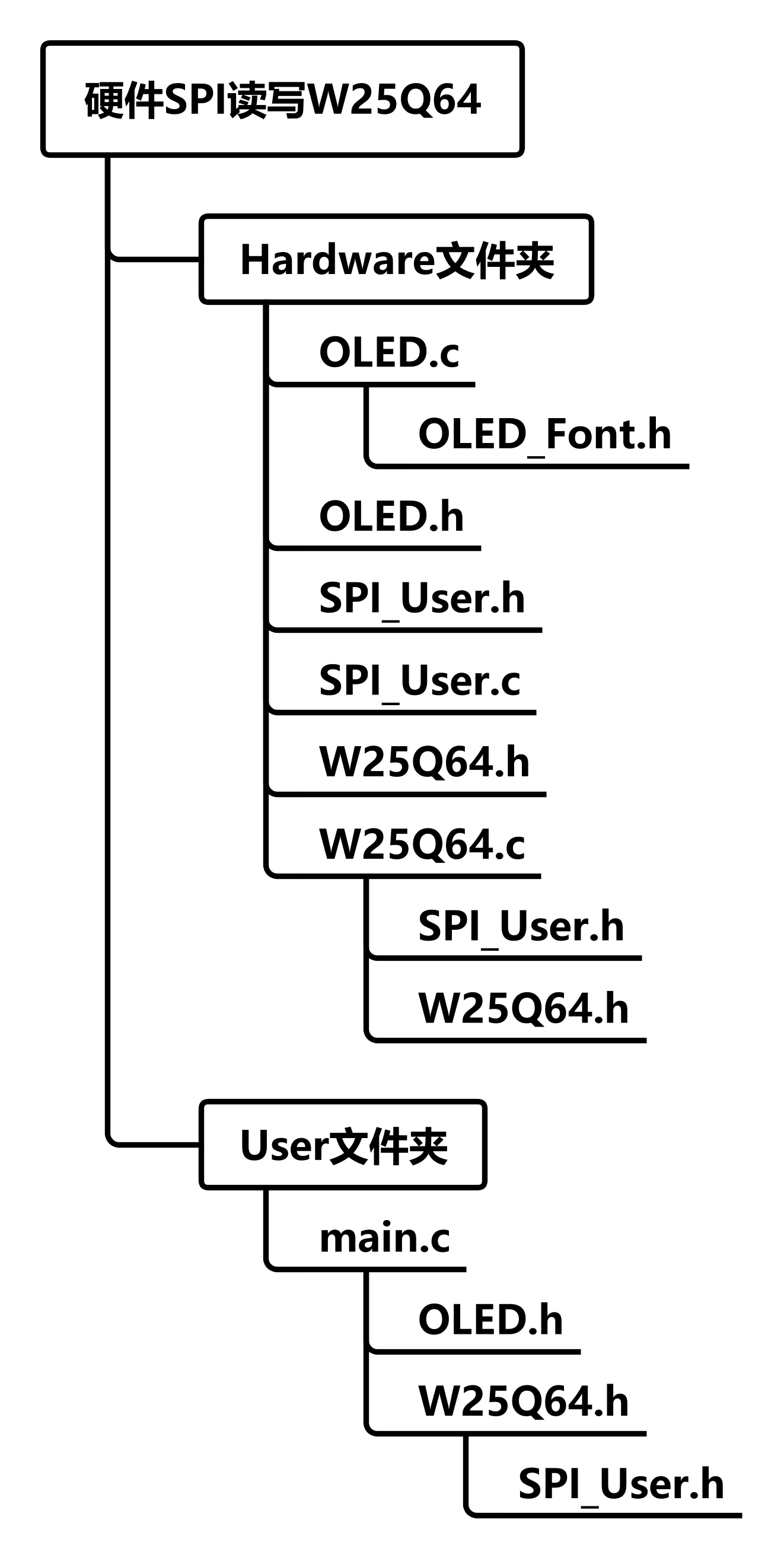
stm32学习笔记-11 SPI通信
11 SPI通信 文章目录 11 SPI通信11.1 SPI通信协议11.2 W25Q64简介11.3 实验:软件SPI读写W25Q6411.4 SPI通信外设11.5 实验:硬件SPI读写W25Q64 注:笔记主要参考B站
江科大自化协 教学视频“
STM32入门教程-2023持续更新中”。 注:…
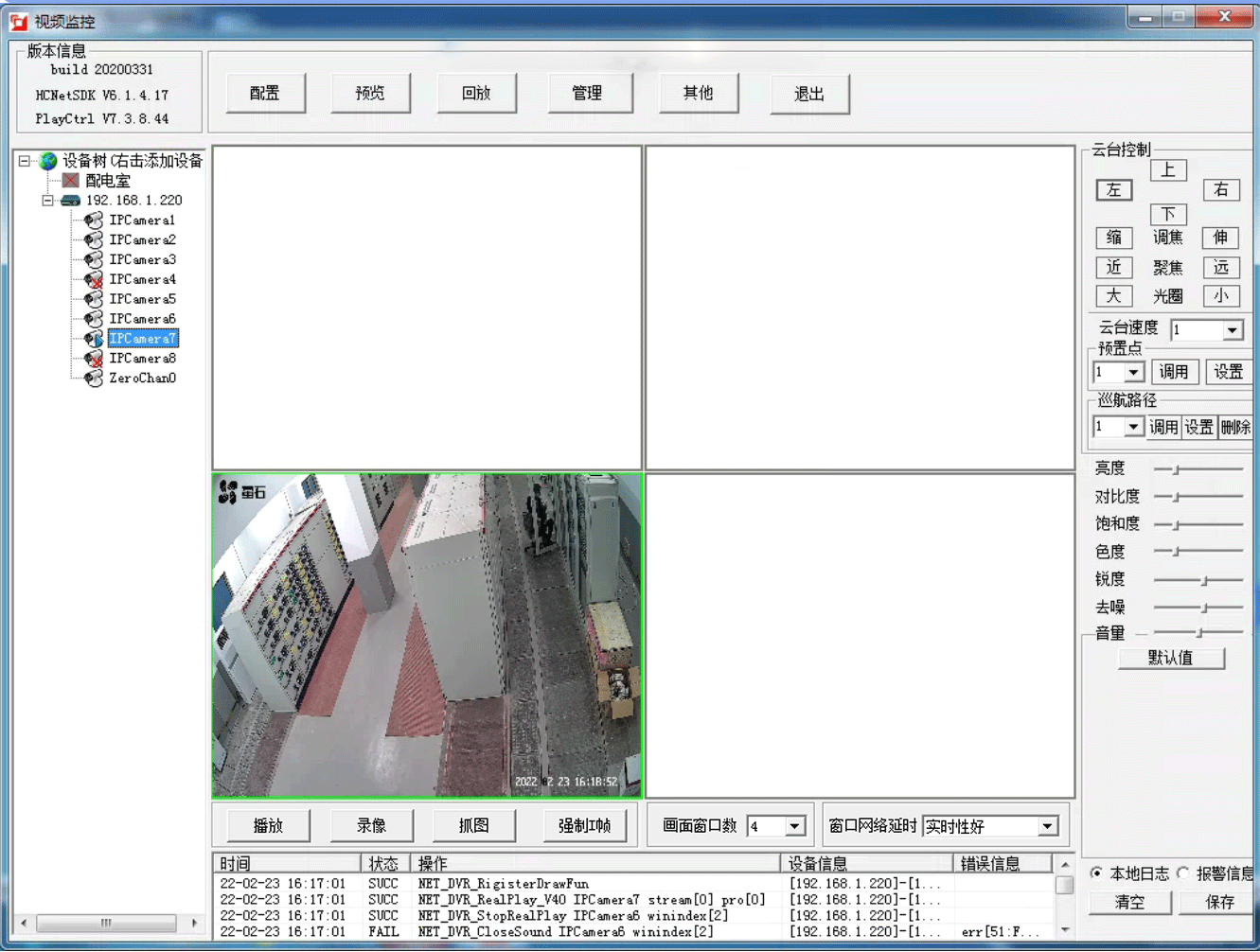
Acrel-2000系列监控系统在亚运手球比赛馆建设
10kV供配电工程中的应用
摘要:智能化配电监控系统是数字化和信息化时代应运而生的产物,已经被广泛应用于电网用户侧楼宇、体育场馆、科研设施、机场、交通、医院、电力和石化行业等诸多领域的高/低压变配电系统中。安科瑞自研的Acrel-2000系列监控系统可监控高压开…
【自动化测试】自动化测试框架那些事儿!
无论是在自动化测试实践,还是日常交流中,经常听到一个词:框架。在教学的过程中,同学们一直对“框架”这个词知其然不知其所以然。
最近看了很多自动化相关的资料,加上一些实践,算是对“框架”有了一些理解…
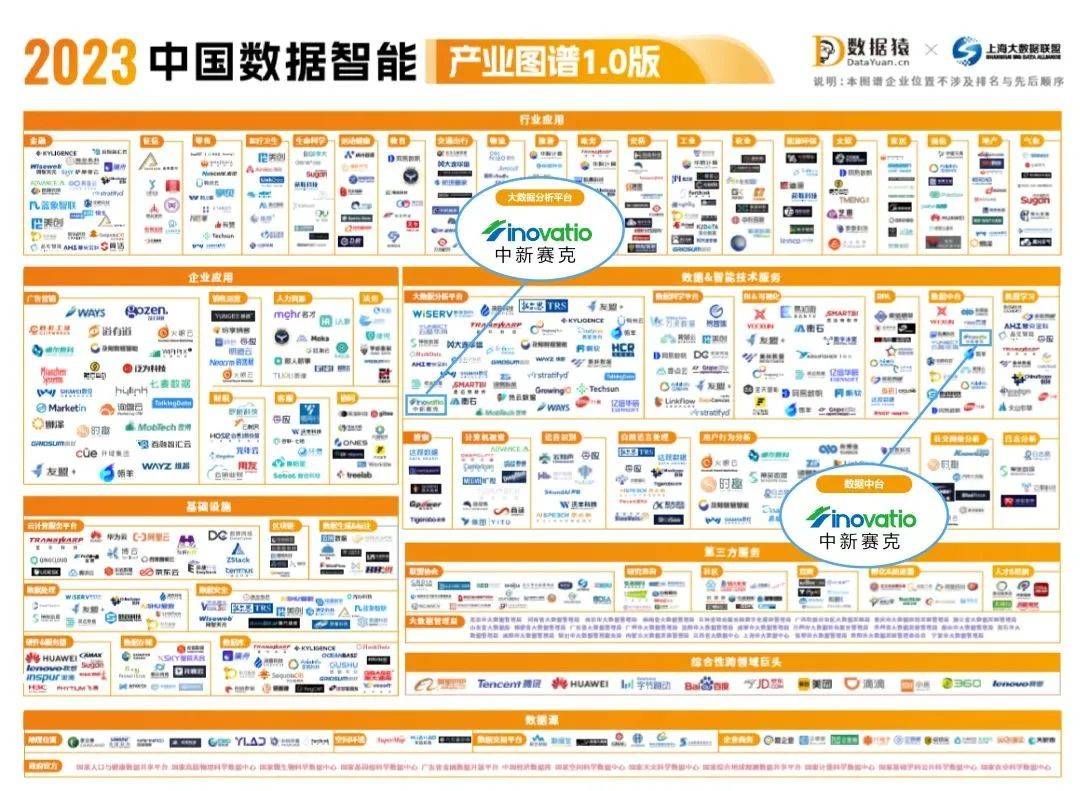
OceanMind海睿思入选《2023中国企业数智化转型全景图中国数据智能产业图谱》
近日,国内知名大数据产业创新服务媒体数据猿携手上海大数据联盟发布了《2023中国企业数智化转型升级服务全景图/产业图谱》和《2023中国数据智能产业图谱》。
两份图谱系统梳理了中国数智化转型升级及数据智能行业发展现状和脉络,评选出极具商业合作价值…
Linux Shell 实现一键部署Oracle21 zip包方式
oracle前言
Oracle开发的关系数据库产品因性能卓越而闻名,Oracle数据库产品为财富排行榜上的前1000家公司所采用,许多大型网站也选用了Oracle系统,是世界最好的数据库产品。此外,Oracle公司还开发其他应用程序和软件。同时&#…
ABeam News|ABeam荣获「SAP BTP 卓越业务分析奖」
近日,「云铸数卯,榫合万象」SAP BTP 客户与生态峰会在桂林圆满落幕。此次年度峰会以全面的视角展现 RISE with SAPSAP BTP如何构建“新型中国企业”数字底座。
ABeam Consulting作为SAP金牌合作伙伴受邀出席,大中华区董事长兼总经理中野洋辅…





![[C语言][典例详解]打印杨辉三角(找规律简单实现)](https://img-blog.csdnimg.cn/478b52802e6d4759b93bd95b40964118.png)