杨辉三角的相关知识

杨辉三角图：

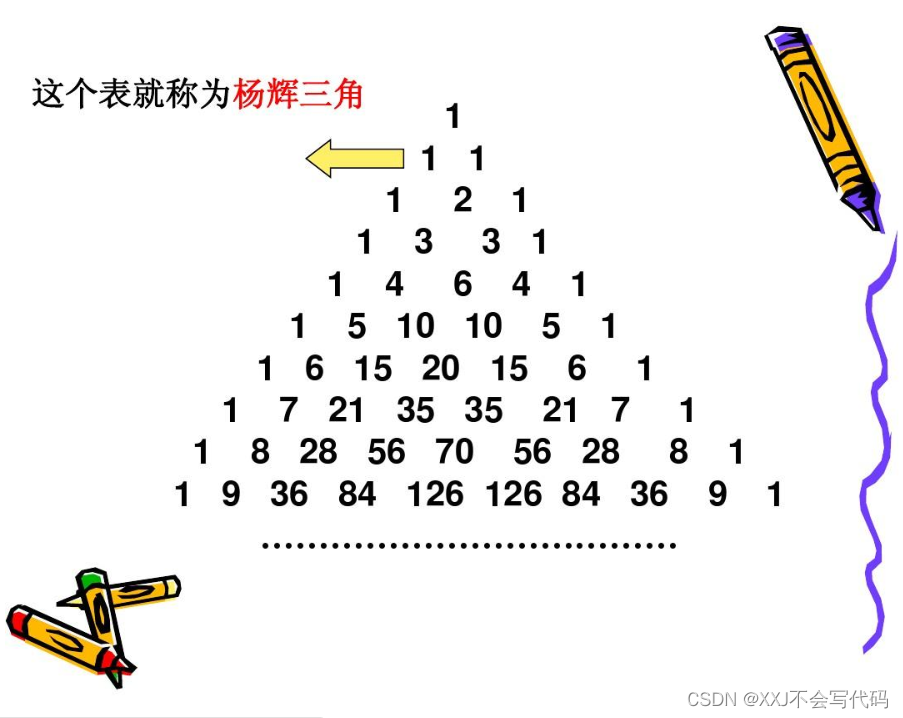
杨辉三角的规律

1.每个数等于它上方两数之和。（如下图1）

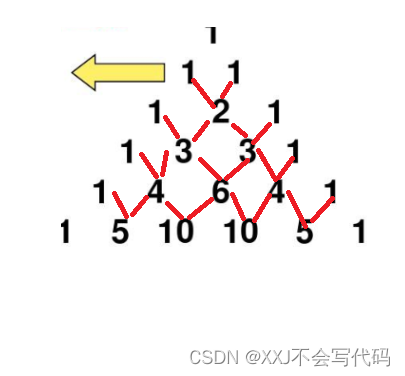
2.每行数字左右对称，由1开始逐渐变大。（如图）

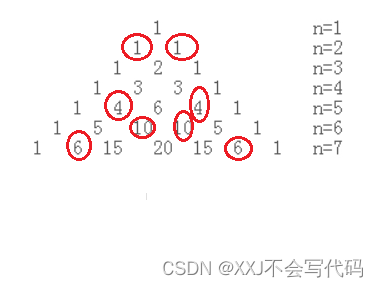
3.第n行的数字有n项。（由上图容易看出）

4.(a+b)^n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。（如图）

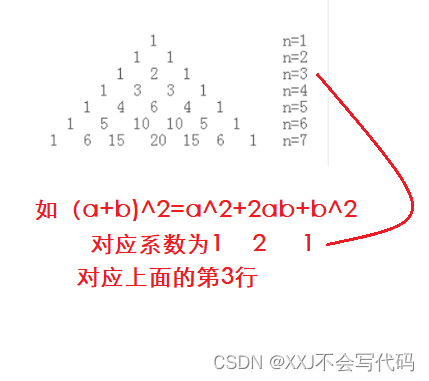
所以我们也可以用二项式来写出，但下面所讲的是用上面行的数字加来得下面所要的数字

在编程中实现

杨辉三角在编程实现中较为容易。最常见的算法便是用上一行递推计算；也有运用和组合的对应关系而使用阶乘计算的，然而后者速度较慢且阶乘容易溢出。

第一步：我们先实现数字的打印，后面再加上空格构成三角形形状；

如：

1.首先我们可以直观的看出三角形的两个斜边都是1；所以我们先打印斜边的1（代码实现+分析+运行效果：）

代码实现：

int main()
{
	int arr[10][10] = { 0 };
	int i = 0;
	for (i=0;i<10;i++)
	{
		arr[i][0] = 1;
		int j = 0;
		for (j = 0; j < i + 1; j++)
		{
			if (i == j)
			{
				arr[i][j] = 1;
			}
		}
	}

	//打印看看效果
	for (i = 0; i < 10; i++)
	{
		int j = 0;
		for (j = 0; j < i + 1; j++)
		{
			printf("%d ",arr[i][j]);
		}
		printf("\n");
	}
	return 0;
}

分析：

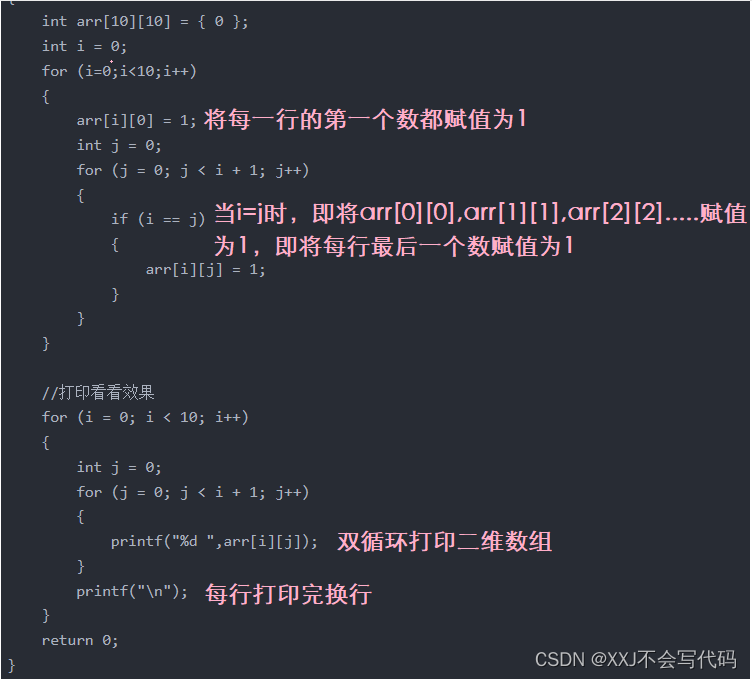
运行效果：

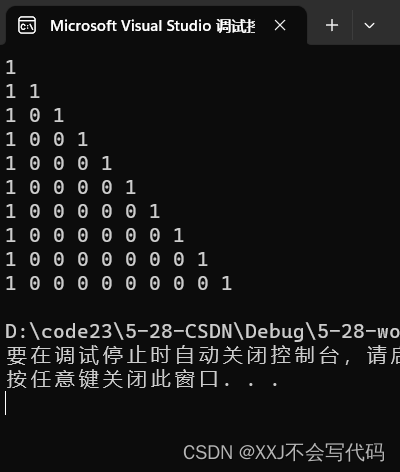
2.打印中间的数据(代码实现+分析+运行效果）

利用上一行的前面一列的数加上一行本列数得到这个数

如：我们要得到第三行的第二个数2 即arr[3][1]；即arr[3-1][1-1]+arr[3-1][1]=arr[3][1]=2

代码实现：

int main()
{
	int arr[10][10] = { 0 };
	int i = 0;
	for (i=0;i<10;i++)
	{
		arr[i][0] = 1;
		int j = 0;
		for (j = 0; j < i + 1; j++)
		{
			if (i == j)
			{
				arr[i][j] = 1;
			}
			if (i > 1 && j > 0)
			{
				arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
			}
			printf("%d ",arr[i][j]);
		}
		printf("\n");
	}
	return 0;
}

代码分析：

运行结果：

第二步：加上空格构成三角形(代码实现+分析+运行效果）

代码实现：

int main()
{
	int arr[10][10] = { 0 };
	int i = 0;
	for (i=0;i<10;i++)
	{
		int n = i;
		arr[i][0] = 1;
		int j = 0;
		for (j = 0; j < i + 1; j++)
		{
			if (i == j)
			{
				arr[i][j] = 1;
			}
			if (i > 1 && j > 0)
			{
				arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
			}
			while (10 - (n + 1))
			{
				printf(" ");
				n++;
			}
			printf("%d ",arr[i][j]);
		}
		printf("\n");
	}
    return 0；
}

代码分析：

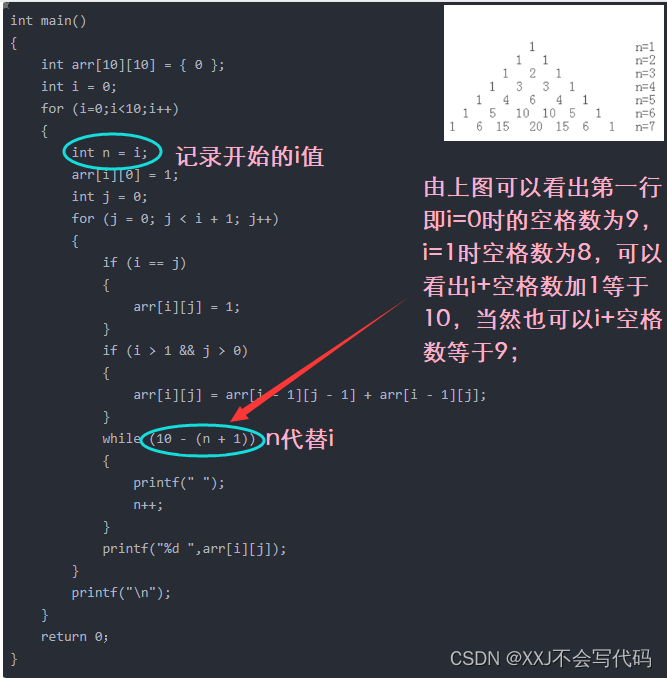
运行结果：

总代码：

int main()
{
	int arr[10][10] = { 0 };
	int i = 0;
	for (i=0;i<10;i++)
	{
		int n = i;
		arr[i][0] = 1;
		int j = 0;
		for (j = 0; j < i + 1; j++)
		{
			if (i == j)
			{
				arr[i][j] = 1;
			}
			if (i > 1 && j > 0)
			{
				arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
			}
			while (10 - (n + 1))
			{
				printf(" ");
				n++;
			}
			printf("%d ",arr[i][j]);
		}
		printf("\n");
	}

	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/584541.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！