1、什么是递归函数

如果一个函数在内部不调用其它的函数，而是自己本身的话，这个函数就递归函数。

遵循：

1. 必须要有出口
2. 每次递归向出口靠近

# 1-10 打印数字
def test(i):

    if i == 10:
        print('10')
    else:
        print(i)
        i += 1
        test(i)
test(1)

# 1-10 的累加和
def test1(i):
    if i == 5:
        return 5
    else:
        return i + test1(i + 1)
r = test1(1)
print(r)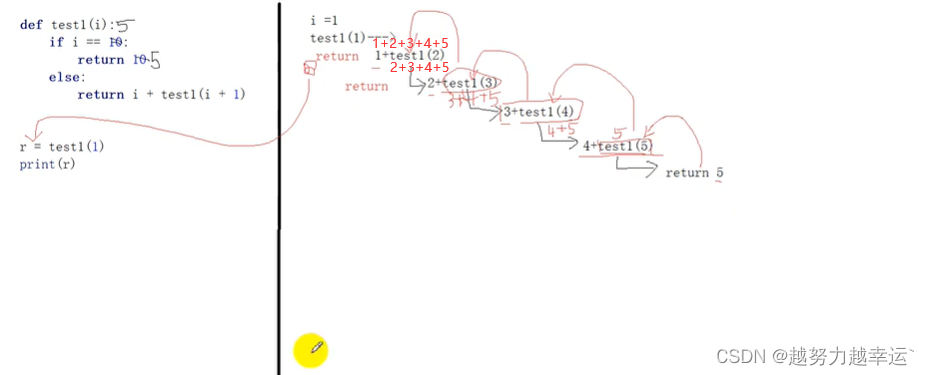

 

2、递归函数的作用

举个例子，计算n！= 1*2*3*…*n

2.1 解决办法1：使用循环来完成

def cal(num):
    result,i = 1,1
    while i <= num:
        result *= i
        i += 1
    return result
print(cal(3))

2.2 看阶乘的规律

1！=1

2！=2 × 1 = 2 × 1！

3！=3 × 2 × 1 = 3 × 2！

4！=4 × 3 × 2 × 1 = 4 × 3！

……

n！=n × （n-1）！

2.3 解决方法2：使用递归来实现

def factorial(num):
    result = 1
    if num == 1:
        return 1
    result = num * factorial(num -1)
    return result
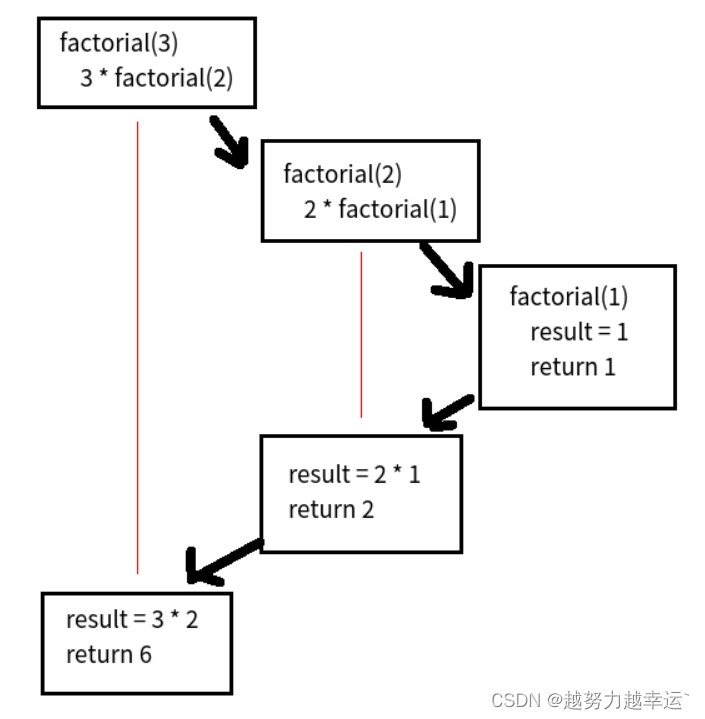
print(factorial(3))

原理

 factorial（3）调用过程：

2.4 练习 

使用递归实现斐波那契数列。1、1、2、3、5、8、13、21、34、……

在数学上，斐波那契数列以如下被递推的方法定义：

F（1）=1，

F（2）=1，

F（n）=F（n-1）+F（n-2）（n>=3,n∈N*）。

代码实现如下：

# 方法一
def my_num(x):
    if x == 1:
        return 1
    elif x == 2:
        return 1
    else:
        return my_num(x-1) + my_num(x -2)

for i in range(1,10):
    print(my_num(i))

# 方法二
def fibo(n):
    "递归函数实现斐波那契数列"
    if n == 1 or n == 2:
        return 1
    else:
        return fibo(n-1) + fibo(n-2)
if __name__ == '__main__':
    n = int(input('请输入数列的项数：'))
    res = fibo(n)
    print(res)

# 一行代码实现斐波那契数列
n = int(input("请输入数列的项数："))
fibo = [x[0] for x in [(a[i][0], a.append([a[i][1], a[i][0]+a[i][1]])) for a in ([[1, 1]], ) for i in range(n)]]
print(fibo)

2.5 问题总结

1、RecursionError: maximum recursion depth exceeded while calling a Python object

• 问题描述：递归超过了最大的深度
• 问题原因：python的递归深度默认为1000。当递归深度超过1000时，就会报错。
• 解决方法：将递归的深度修改的大一些

  import sys 
  sys.setrecursionlimit(100000)
  

• 查看递归层数

  def recursion(depth):
      depth += 1
      print(depth)
      recursion(depth)
  
  recursion(0)