一.基本理念

粒子群算法(PSO),最早由两位外国科学家在1995年提出，该算法源自对鸟类捕食问题的研究。

我们将鸟类补食性原则分为一下三个基数，每组基数对应一个粒子，而每组粒子我们将其称之为种群。所以我们将其在细分具体，基数一，为我们当前粒子的位置，基数二，为我们当前粒子的速度，基数三，为我们当前粒子的适应度值(这里的适应度值则是由我们当前的位置和速度综合求解得出的结果，对于每一个问题的自适应度值的求解过程都是不一样的)。

我们的每一个粒子都将其放入解空间中，在我们的解空间中，我们的粒子的每一代都得保留最优个体(Pbest)，和最优种群值(Gbest)，通过跟踪我们的最优粒子来更新最优位置，这里我们解释一个Pbest，是我们个体对应最优适应度值的最优位置，而Gbest是指种群中最优适应度值对应的最优位置。

我们对于每次的更新过程是通过比较新粒子的适应度值和个体极值，群体极值的适应度值更新最优个体(Pbest)和群里最优值(Gbest)。

二.更新函数

其中V是我们的每一次迭代更新的速度，X是每一次要更新的位置，Pid，和Pgd分别为个体最优值，和群体最优值。w，c1,c2为常数。这里的w是一个很关键的值，它在迭代更进过程会随着迭代次数的变化而变化，会导致两边的权值发生差异。但目前我们只将其设为常数，不考虑权值的变化。

三.具体实验步骤

四.样例举例

一元函数的优化过程

1.初始化过程

我们设定x=1：0.01：2 这是我们x的取值范围和移动精度。

设定y=sin(10pix)./x 这是我们对应的函数移动趋向。

我们当前要解决的问题我们要求出对应精度，y的最大值，所以我们的最优值，求的就是x在y上的最大分布。

参数初始化

c1=1.49445 c2=1.49445 这里的两个参数，我们是随便定义的。

maxgen=50 sizepop=10 分别定义我们的进化次数和种群规模

Vmin=-0.5 Vmax=0.5 速度的偏移范围

popmin=1 popmax=2 x也就是我们位置的范围变化

初始化粒子基数（生成我们第一代粒子的位置和速度）

for i=1:sizepop
   %%我们随机产生一个种群
   pop(i,:)=(rands(1)+1)/2+1;%%这里的随机数生成方式是为了保证我们生成的数能够在我们的位置范围中。
   %%我们的pop中的每一行都保留一个个体的当前的x位置
   V(i,:)=0.5*rand %%这里我们随机化每个粒子的速度
   %%V这里的每一行我们表示当前粒子的速度
   fitness(i)=sin(10*pop(i,:)./pop(i,:))
   %%在这里我们的自适应度值就是我们当前位置对应的函数值
end

个体最优值和群体最优值的初始化更新

%%bestfitness我们的群体最优适应度的值
%%bestindex ↑其对应的下标
[bestfitness,bestindex]=max(fitness);%%我们得出我们的最大适应度和其下标
%%zbest 这里是我们的全局最佳个体
%%gbest 这里是我们的每个个体对应的最优值
zbest=pop(bestindex,:)
gbest=pop
fitnesszbest=bestfitness  %%群体中的最优适应度值
fitnessgbest=fitness %%每个个体的最优适应度值

2.进化代数寻优过程

for i=1:maxgen %%最大代数寻优
    for j=i:sizepop
    %%我们先进行速度的更新
    %%根据我们的速度公式
    V(j,:)=V(j,:)+c1*rand*(gbest(j,:)-pop(j,:))+c2*rand*(zbest-pop(j,:))
    %%c1*rand*(gbest(j,:)-pop(j,:))%%个体最优位置减去每个个体的位置 
    %%c2*rand*(zbest(j,:)-pop(j,:))%%群体最优位置减去每个个体的位置
    %%为了保证我们个体速度的范围
    V(j,find(V(j,:)>Vmax))=Vmax;
    V(j,find(V(j,:)<Vmin))=Vmin;
    %%种群位置的更新 (速度和位置先后更新次序不可颠倒)
    pop(j,:)=pop(j,:)+V(j,:);%%更据我们的公式我们得出
    %%同时我们保证位置的范围是否超出
    pop(j,find(pop(j,:)>popmax)) = popmax;%%局限最大
    pop(j,find(pop(j,:)<popmin)) = popmin;%%局限最小
    fitness(j)=fun(pop(j,:));%%对于每一个位置的适应度更新
    %%这里我们的fun函数返回就是x对于在y上的位置
    end
    for j=1:sizepop
    %%在我们将个体位置，群体位置，还有每个位置的适应度得出后，我们还有对个体最优进行更新
       if fitness(j)>fitnessgbest(j)
         gbest(j,:)=pop(j,:)%%保留最优位置%%每个个体
         fitnessgbest(j)=fitness(j);%%保留最优适应度值%%每个个体
       end
    %%在将gbest和fitnessgbest更新完毕之后我们在将群体最优位置和群体最优适应度更新了
       if fitness(j)>fitnesszbest
         zbest=pop(j,:);
         fitnesszbest=fitness(j);
       end
    end
    hold on
    plot(gbest,fitnessgbest,'r*')%%将粒子的走向绘出
    yy(i)=fitnesszbest%%保留种群最优值，之后将其绘图用于识别适应代数和适应度变化的趋势
end

3.将结果进行绘图用于直观的看出粒子的走向和，进化代数和适应度的变化

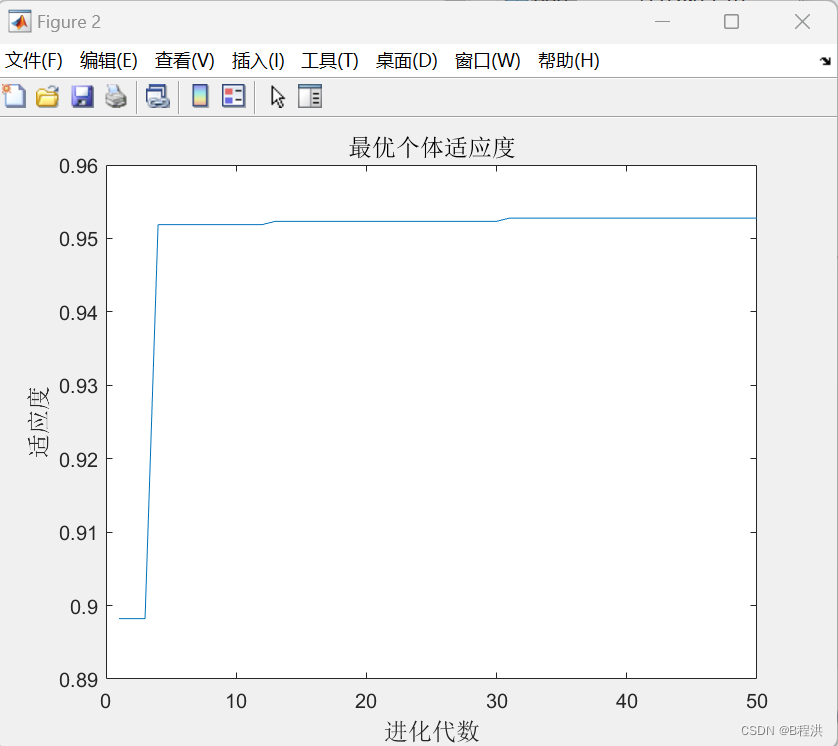
hold on
plot(zbest,fitnessbest,'r*')%%输出我们群体最优值的对于的点


figure
%%直观的查看每一代的适应度是如何变化的
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);