一、树结构

二叉树、二叉查找树、平衡二叉树、红黑树

1、数据结构遍历方式

1、前序遍历：当前节点、左子节点、右子节点
2、中序遍历：左子节点、当前节点、右子节点
3、后序遍历：左子节点、右子节点、当前节点
4、层序遍历：一层一层的遍历

2、数据结构（平衡二叉树）

（1）规则：任意节点左右子树高度差不超过1

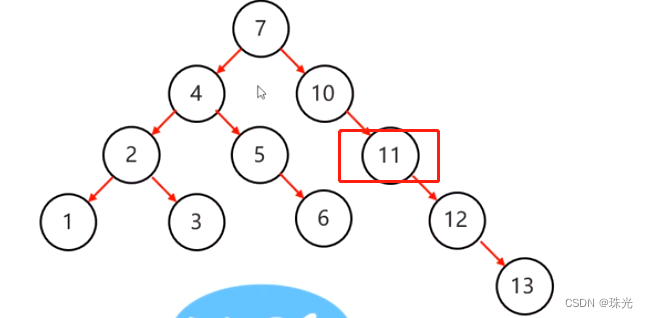
在这里插入图片描述

（2）旋转机制：

左旋
右旋

处发机制：当添加一个节点后，该树不再是一个平衡二叉树

左旋旋转步骤：
1.确定支点：从添加的节点开始，不断的往父节点找不平衡的节点
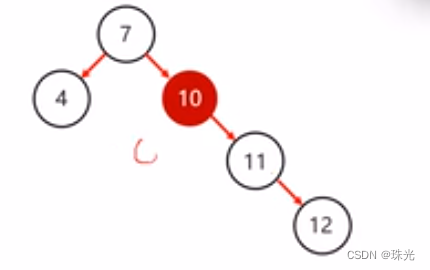
在这里插入图片描述
2.把支点左旋降级，变成左子节点
3.晋升原先的右子节点

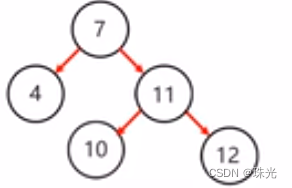
右旋旋转步骤：
1.确定支点：从添加的节点开始，不断的往父节点找不平衡的节点
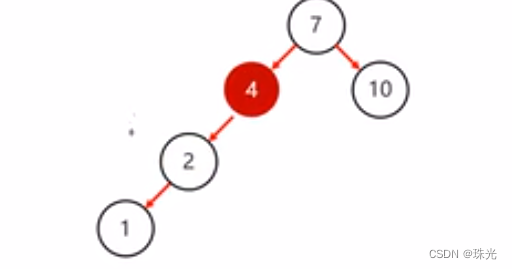
在这里插入图片描述
2.把支点右旋降级，变成右子节点
3.晋升原来的左子节点

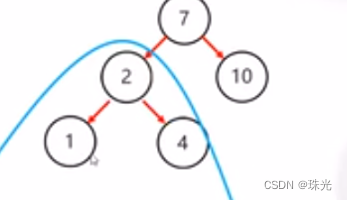
（3）数据结构 (平衡二叉树 )需要旋转的四种情况

（1）左左：一次右旋
（2）左右：先局部左旋，再整体右施
（3）右右：一次左旋
（4）右左：先局部右旋，再整体左旋

左左：当根节点左子树的左子树有节点插入，导致二叉树不平衡
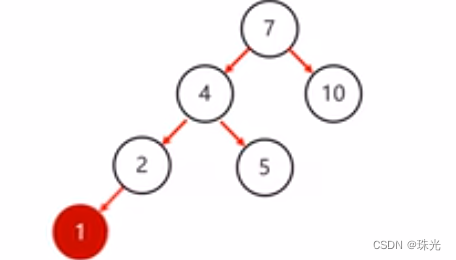
在这里插入图片描述
左右：当根节点左子树的右子树有节点插入，导致二叉树不平衡

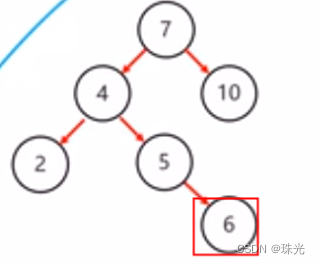
右右：当根节点右子树的右子树有节点插入，导致二叉树不平衡

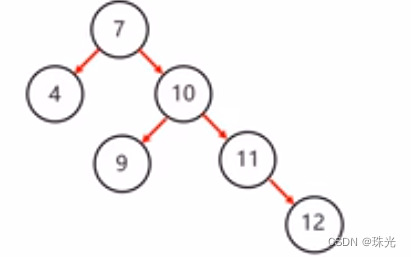
右左：当根节点右子树的左子树有节点插入，导致二叉树不平衡

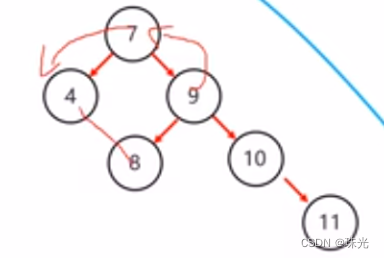
3、数据结构（红黑树）

（1）介绍

红黑树是一种自平衡的二叉查找树，是计算机科学中用到的一种数据结构。
1972年出现，当时被称之为平衡二叉B树。后来，1978年被修改为如今的"红黑树"。
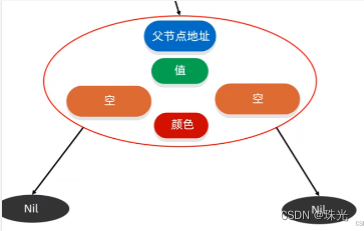
它是一种特殊的二叉查找树，红黑树的每一个节点上都有存储位表示节点的颜色
每一个节点可以是红或者黑；红黑树不是高度平衡的，它的平衡是通过"红黑规则"进行实现的

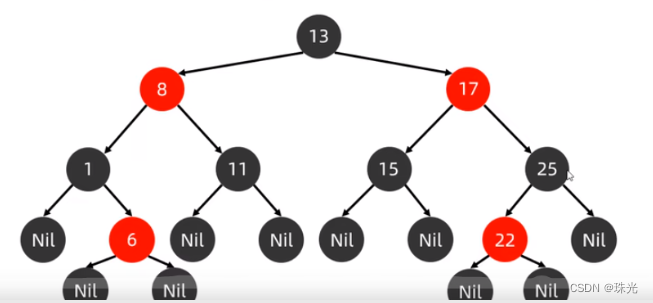
红黑树：
是一个二叉查找树
但是不是高度平衡的
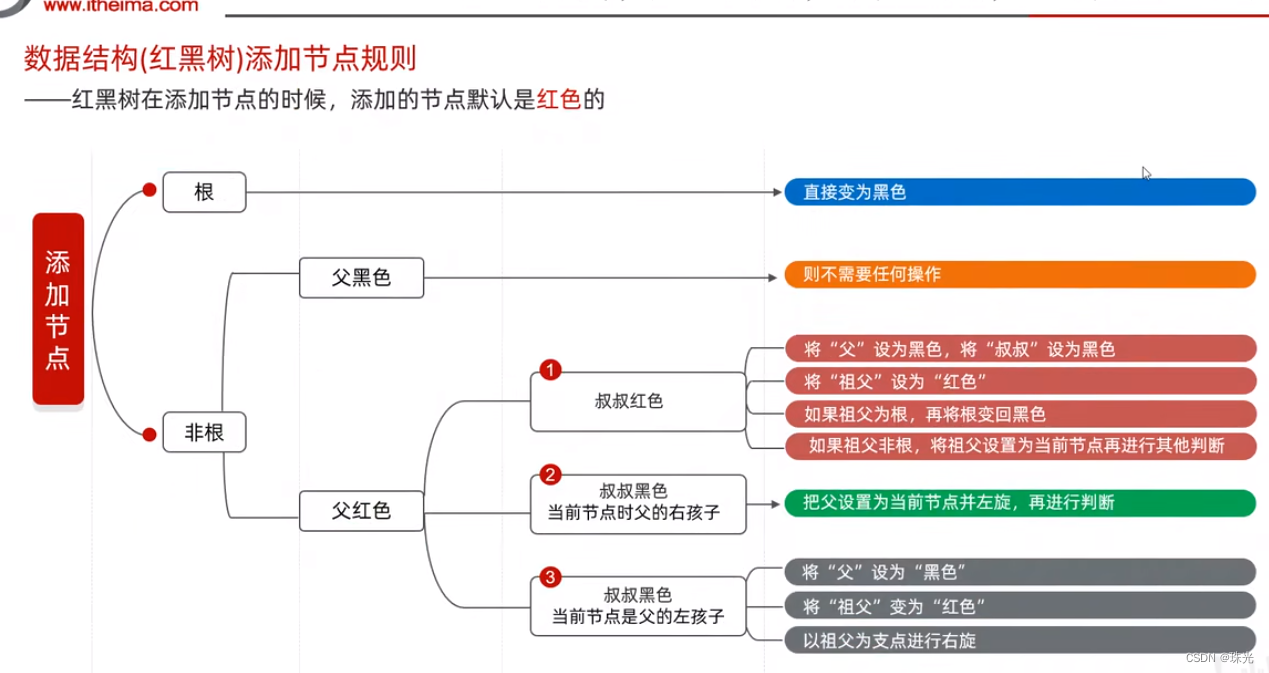
添加节点默认是红色的（效率高）
条件：特有的红黑规则

（2）红黑规则

每一个节点或是红色的，或者是黑色的
根节点必须是黑色
如果一个节点没有子节点或者父节点，则该节点相应的指针属性值为NiL，这些NiL视为叶节点，每个叶节点(NiL)是黑色的
如果某一个节点是红色，那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)
对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点

二、集合

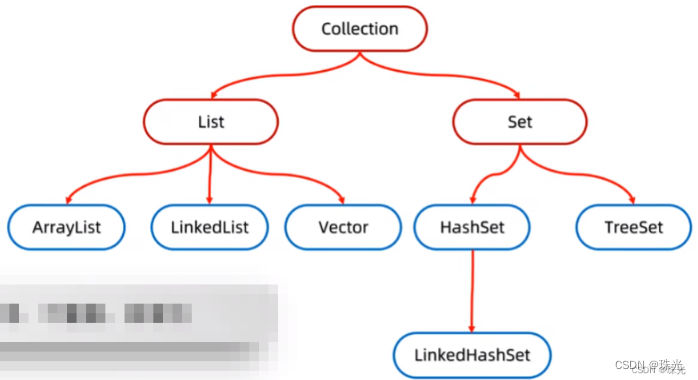
在这里插入图片描述
List系列集合：添加的元素是有序、可重复、有索引
Set系列集合：添加的元素是无序、不重复、无索引

1、Collection遍历方式

（1）迭代器遍历

迭代器在Java中的类是lterator，迭代器是集合专用的遍历方式

Iterator<String> it = list.iterator();
while(it.hasNext()){
	String str = it.next();
	System.out.printIn(str);
}

选代器的四个细节

如果当前位置没有元素，还要强行获取，会报NoSuchElementException
迭代器遍历完毕，指针不会复位
循环中只能用一次next方法
迭代器遍历时，不能用集合的方法进行增加或者删除

（2）增强for遍历

增强for的底层就是迭代器，为了简化迭代器的代码书写的。
所有的单列集合和数组才能用增强for进行遍历。

for (String s : list) {
	System.out.println(s);
}

（3）Lambda表达式遍历

coll.forEach(s -> System.out.printIn(s));

2、List集合

有序、有索引、可重复

（1）独特方法

方法名称	说明
void add(int index,E element）	在此集合中的指定位置插入指定的元素
E remove(int index)	删除指定索引处的元素，返回被删除的元素
E set(int index,E element)	修改指定索引处的元素，返回被修改的元素
E get(int index)	返回指定索引处的元素

（2）注意细节

list集合 {1，2，3} ，执行list.remove(1)
请问: 此时删除除的是1这个元素，还是1索引上的元素?
因为在调用方法的时候，如果方法出现了重戟现象，优先调用，实参跟形参类型一致的那个方法。
list,remove(1); 删除的是元素2（索引1）
如果手动装箱，手动把基本数据类型的1，变成Integer类型
Integer i = Integer.valueof(1);
list.remove(i); 删除的是元素1（索引0）

（3）集合的遍历方式

迭代器遍历
列表迭代器遍历
增强for遍历
Lambda表达式遍历
普通for循环(因为List集合存在索引)

// 5.列表迭代器
//获取一个列表迭代器的对象，里面的指针默认也是指向0索引的
ListIterator<String> it = list.listIterator();
while(it.hasNext()){
	String str = it.next();
	System.out.println(str);
}


//额外添加了一个方法: 在遍历的过程中，可以添加元素
ListIterator<String> it = list.listIterator();
while(it.hasNext()){
	String str = it.next();
	if("bbb".equals(str)) {
		it.add("qqq");
	}
}
System.out.printIn(list);

遍历方式	说明
迭代器遍历	在遍历的过程中需要删除元素，请使用迭代器
列表迭代器	在遍历的过程中需要添加元素，请使用列表迭代器
增强for遍历 / Lambda表达式	仅仅想遍历，那么使用增强for或Lambda表达式
普通for	如果遍历的时候想操作索引，可以用普通for。

3、ArrayList

（1）细节

利用空参创建的集合，在底层创建一个默认长度为0的数组
添加第一个元素时底层会创建一个新的长度为10的数组
存满时，会扩容1.5倍
如果一次添加多个元素，1.5倍还放不下，则新创建数组的长度以实际为准

（2）源码

在这里插入图片描述

4、 LinkedList

底层数据结构是双链表，查询慢，增删快，但是如果操作的是首尾元素，速度也是极快的。
在这里插入图片描述
源码：

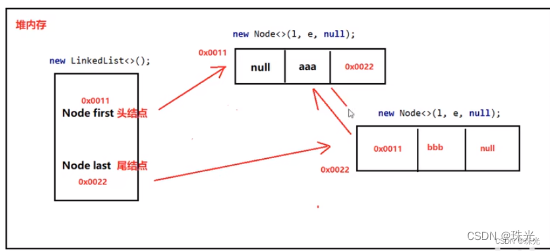
迭代器底层逻辑
在这里插入图片描述

5、泛型

（1）定义

泛型：是JDK5中引入的特性，可以在编译阶段约束操作的数据类型，并进行检查
泛型的格式：<数据类型>
注意：泛型只能支持引用数据类型

没有泛型的时候，集合如何存储数据？
结论：
如果我们没有给集合指定类型，默认认为所有的数据类型都是object类型。此时可以往集合添加任意的数据类型。带来一个坏处：我们在获取数据的时候，无法使用他的特有行为。

此时推出了泛型，可以在添加数据的时候就把类型进行统一。而且我们在获取数据的时候，也省的强转了，非常的方便。

（2）泛型的好处

统一数据类型。
把运行时期的问题提前到编译期间，避免了强制类型转换可能出现的异常，因为在编译阶段类型就能确定下来。

Java中的泛型是伪泛型：
Java文件中创建了泛型，但是Class文件中没有泛型，ArrayList list = new ArrayList(); 。这种情况叫做泛型的擦除

（3）泛型的细节

泛型中不能写基本数据类型
指定泛型的具体类型后，传递数据时，可以传入该类类型或者其子类类型
如果不写泛型，类型默认是Object

（4）泛型定义

类后面 → 泛型类
方法上面 → 泛型方法
接口后面 → 泛型接口

泛型类

使用场景：当一个类中，某个变量的数据类型不确定时，就可以定义带有泛型的类
格式：

修饰符  class  类名<类型> {

}

public class ArrayList<E> {
		//        创建对象时，E就确定类型
		
}

注意：此处E可以理解为变量，但是不是用来记录数据的，而是记录数据的类型，可以写成：T、E、K、V等

泛型方法

方法中形参类型不确定时，方案

使用类名后面定义的泛型，所有方法都能用
在方法什么上定义自己的泛型，只有本方法能用

格式

修饰符 <类型> 返回值类型  方法名(类型 变量名) {

}

public <T> void show(T t) {
}

泛型接口

格式：

修饰符  interface 接口名<类型> {

}

public interface List<E> {
}

如何使用泛型接口？

实现类给出具体类型
实现类延续泛型，创建对象时再确定

（5）泛型的继承和通配符

泛型不具备继承性，但是数据具备继承性

此时我们就可以使用泛型的通配符：
? 也表示不确定的类型，他可以进行类型的限定

? extends E：表示可以传递E或者E所有的子类类型
? super E：表示可以传递E或者E所有的父类类型

（6）应用场景:

如果我们在定义类、方法、接口的时候，如果类型不确定，就可以定义泛型类、泛型方法、泛型接口。
如果类型不确定，但是能知道以后只能传递某个继承体系中的，就可以泛型的通配符泛型的通配符:
关键点:可以限定类型的范围。

6、Set

（1）特点

set系列集合：添加的元素是无序、不重复、无索引

无序：存取顺序不一致
不重复：可以去除重复
无索引：没有带索引的方法，所以不能使用普通for循环遍历，也不能通过索引来获取元素

（2）set集合的实现类

HashSet:无序、不重复、无索引
LinkedHashSet: 有序、不重复、无索引
TreeSet:可排序、不重复、无索引

（3）存储字符串并遍历

利用Set系列的集合，添加字符串，并使用多种方式遍历。

选代器
增强for
Lambda表达式

7、HashSet底层原理

HashSet集合底层采取哈希表存储数据，哈希表是一种对于增删改查数据性能都较好的结构
哈希表组成：

JDK8之前：数组+链表
JDK8开始：数组+链表+红黑树

哈希值：对象的整数表现形式

根据hashCode方法算出来的int类型的整数
该方法定义在object类中，所有对象都可以调用，默认使用地址值进行计算
一般情况下，会重写hashCode方法，利用对象内部的属性值计算哈希值

对象的哈希值特点

如果没有重写hashCode方法，不同对象计算出的哈希值是不同的
如果已经重写hashcode方法，不同的对象只要属性值相同，计算出的哈希值就是一样的
在小部分情况下，不同的属性值或者不同的地址值计算出来的哈希值也有可能一样。(哈希碰撞)

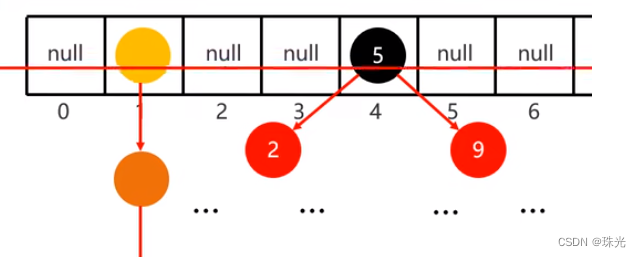
HashSet 底层原理

创建一个默认长度16，默认加载因子（数组扩容使用）为0.75的数组，数组名table
根据元素的哈希值跟数组的长度计算出应存入的位置； int index = (数组长度 - 1) & 哈希值
判断当前位置是否为null，如果是null直接存入
如果位置不为null，表示有元素，则调用equals方法比较属性值
如果一样，则不存该元素；不一样，则存入数组，形成链表
JDK8以前：新元素存入数组，老元素挂在新元素下面
JDK8以后：新元素直接挂在老元素下面，当链表长度超过8，而且数组长度大于等于64时，自动转换为红黑树

在这里插入图片描述

8、LinkedHashSet

（1）底层原理

有序、不重复、无索引。
这里的有序指的是保证存储和取出的元素顺序一致
原理：底层数据结构是依然哈希表，只是每个元素又额外的多了一双链表的机制记录存储的顺序。

（2）总结

在以后如果要数据去重，我们使用哪个?
默认使用HashSet。如果要求去重且存取有序，才使用LinkedHashSet

9、TreeSet

（1）特点

不重复、无索引、可排序
可排序：按照元素的默认规则 (有小到大)排序
TreeSet集合底层是基于红黑树的数据结构实现排序的，增删改查性能都较好

（2）默认的规则

对于数值类型：Integer，Double，默认按照从小到大的顺序进行排序
对于字符、字符串类型：按照字符在ASCII码表中的数字升序进行排序

（3）两种比较方式

默认排序/自然排序：Javabean类实现Comparable接口指定比较规则

public class Student implements Comparable<Student>(
	private String name;
	private int age;

	@Override
	public int compareTo(Student o) (
		//指定排序的规则
		//只看年龄，我想要按照年龄的升序进行排列
		// this: 表示当前要添加的元素 o:表示已经在红黑树存在的元素
		// 返回值: 负数:认为要添加的元素是小的，存左边；正数:认为要添加的元素是大的，存右边； 0：认为要添加的元素已经存在，舍奔
		return this .getAge() - o.getAge()
	}
}

比较器排序：创建TreeSet对象时候，传递比较器Comparator指定规则

	//1.创建集合
	TreeSet<String> ts = new TreeSet<>(new Comparator<String>() {
		@Override
		public int compare(String o1, String o2) {
			public 0;
		}
	});

（4）总结

TreeSet集合的特点是怎么样的?
可排序、不重复、无索引
底层基于红黑树实现排序，增删改查性能较好
TreeSet集合自定义排序规则有几种方式
方式一: Javabean类实现Comparable接口，指定比较规则
方式二: 创建集合时，自定义Comparator比较器对象，指定比较规则
方法返回值的特点
负数: 表示当前要添加的元素是小的，存左边
正数:表示当前要添加的元素是大的，存右边
0 :表示当前要添加的元素已经存在，舍弃