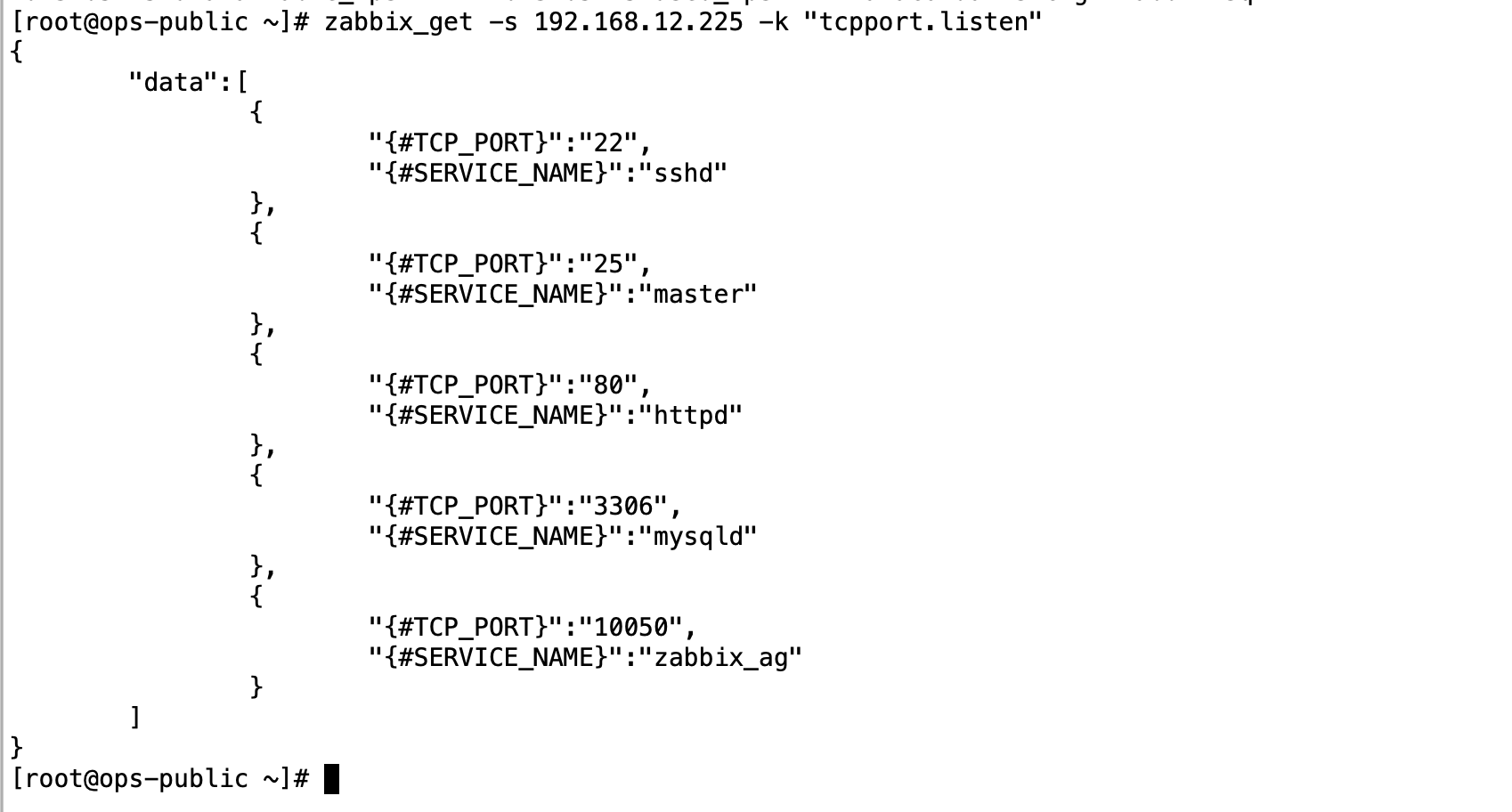
算法分析

 首先，前序是按照 根 -> 左子树 -> 右子树   这样的顺序来进行访问的，也就是说，前序给出的顺序一定是先给出根结点的，那么我们就可以根据前序的顺序来依次递归判断出每个子树的根结点了。

如下所示：

 我们依次向后遍历，就先遍历的根结点，然后在从左子树，和右子树当中来寻找每个子树的根节点。那么我们就可以依次以前序的根节点，从中序当中找出最大的根结点，依此来找出这个根节点对应的左子树和右子树;

 如上图，中序中：在根结点左边的结点就是这个根结点对应的左子树的所有结点，在根结点右边的结点就是这个根结点对应的右子树的所有结点。

 由上述的单趟的算法，我们可以递归思想，一层递归判断一个根节点，这样，我们就可以判断所有的根结点的所有左子树和右子树了。

 那么，每一次由根结点所分出来的左子树和右子树的结点，我们可以看做是两个区间，这两个区间就是每一次由根结点分割出来的左子树区间和右子树区间。比如，在左子树区间当中，因为前序的从左向右我们可以依次来找出 根结点。如上述，我们第一趟找出的是 A 这个结点是这个整个数的根节点，那么 B 就是这个 A 这个根结点的左子树的根结点，如下图所示：

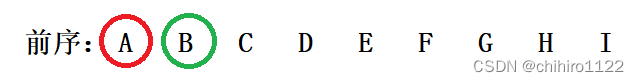
 我们在中序当中，循环找出这个 B 这个根结点的 左右子树，如下图所示，用绿色横线表示：

 由 B 这个结点，我们又划分出了两个区间，这两个区间分别是 B 的左子树区间和 右子树区间。

我们还可以继续在 B 的左子树区间和右子树区间当中去递归，继续寻找出其他的根结点，和这个根结点对应的 左子树 和 右子树。

往后的两趟如下所示（我们这里创建二叉树的顺序类似于 前序的 方式创建）：

 第三趟：

 第四趟：

 

 当我们访问到这个左右子树都为空的时候就停止递归，并在  return 返回的时候，把这个根结点的 left 和 right 指针置NULL。

基本思想我们了解了，这里主要的创建二叉树的方式就是使用 前序的顺序，来从 前序和中序的顺序当中，一次找出这个根结点，在由这个根结点 分割出两个区间，这个两个区间就是这个 根结点对应的 左子树区间和 右子树区间。

现在主要的问题就是，有一个根结点分割的 左右区间的 范围如果确定？

我们在上述的单趟算法描述的时候，提到了我们要循环找到，前序当中找到的根结点，在存储中序的数组当中的下标位置。这个下标位置很重要，我们要根据这个下标来找出这个 ，每一趟 存储前序数组的区间， 和 存储中序数组的区间。

我们首先来看  存储中序数组的区间：

首先，我们是使用 循环从 前序区间的第一个 结点在中序当中 存储的下标位置（num），那么我们就知道，在 递归左子树 存储中序的数组区间就是 【 L2, num - 1】。其中 L2 是 存储中序数组的，这一层递归的 左区间，因为是左子树递归，所以这个左区间保存；而右区间，要因为 根结点而进行分割，所以是 num 根结点 位置的前一个位置。

而 递归右子树的 存储中序数组的区间应该是 【num + 1, R2】、 。其中 R2 是 存储中序数组的，这一层递归的 有区间，因为是递归右子树，所以有区间不变；而左区间因为 根结点的分割，变成 num 根结点位置的下一个位置。

存储前序数组的区间：

因为由一个 根节点 分出来的左右区间当中的结点个数是相同的，所以，在前序，中序当中的 左区间 和 右区间当中的结点个数也应该是 对应相等的。

 也就是： 前序 左子树区间结点个数 =  中序 左子树区间结点个数；

前序 右子树区间结点个数 = 中序 右子树区间结点个数。

 根据上述，那么 前序 左子树区间 【L1 + 1  ,  L1 + 中序左子树区间的结点个数】，左区间是 L1 + 1 是因为，前序的左区间，要向右来依次递归在中序当中找出根结点 存储 的下标； 那么 左区间 + 区间结点个数  就是 前序 左子树区间。即 【L1 + 1, num + L1 - L2】

根据上述的类似思想，不难推出 前序 的 右子树区间 为：【R1 - 中序右子树区间的结点个数 ,  R1】 , 即 【 num + 1 + R1 - R2 , R1】

 那么代码具体实现，我们采用在函数递归之时，传入当前结点的  left 孩子指针，或者是 right 孩子指针，然后再下一层递归函数当中，创建这个结点的空间，给这个空间结点当中的结点赋值。

 如下所示：

(*Tree) = BuyTreeNode(first[L1]);// 创建一个新的结点

// 递归左子树（构建左子树）
Order_CteatTree(&(*Tree)->left, first, second, L1 + 1, num + L1 - L2 , L2, num - 1);
// 递归右子树（创建右子树）
Order_CteatTree(&(*Tree)->right, first, second, num + 1 + R1 - R2 , R1 , num + 1, R2);

 那么递归的结束条件是，当我们递归到这个区间，不再合法的时候就代表这个 根结点的对应这个区间 已经为空了，没有结点了。代码如下：
 

	if (L1 > R1 || L2 > R2)
	{
		(*Tree) = NULL;
		return;
	}

 创建二叉树的完整代码：

void Order_CteatTree(BTNode** Tree,char* first, char* second, int L1, int R1, int L2 ,int R2)
{
// 递归的结束条件，当区间不在合法的时候，代表这个结点已经不再有孩子结点了
	if (L1 > R1 || L2 > R2)
	{
		(*Tree) = NULL;
		return;
	}
	
	(*Tree) = BuyTreeNode(first[L1]);// 创建一个新的结点

	int num = 0;
	for (num; num < R2; num++)
	{
		if (first[L1] == second[num])
		{
			break;
		}
	}

	Order_CteatTree(&(*Tree)->left, first, second, L1 + 1, num + L1 - L2 , L2, num - 1);
	Order_CteatTree(&(*Tree)->right, first, second, num + 1 + R1 - R2 , R1 , num + 1, R2);
}

如上就是我们所实现的 根据前序和中序来创建二叉树。

我们用 后序 和 层序 来输出一下这个二叉树，来验证一下这个二叉树是否合法：
 

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#include <string.h>

// 二叉树结点的结构体
typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

// 队列的链式结构实现
typedef BTNode* QDatatype;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDatatype data;
}QueueNode;

// 队列的结构体定义
typedef struct Queue
{
	QueueNode* head;
	QueueNode* tail;
	int size;
}Queue;

// 队列的初始化
void QueueInit(Queue* pq)
{
	assert(pq);

	pq->head = pq->tail = NULL;
	pq->size = 0;
}

// 队列的销毁
void QueueDestroy(Queue* pq)
{
	assert(pq);

	QueueNode* cur = pq->head;
	while (cur)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur->next;
	}

	pq->head = pq->tail = NULL;
	pq->size = 0;
}


// 队列的插入
void QueuePush(Queue* pq, QDatatype x)
{
	assert(pq);

	QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newNode == NULL)
	{
		perror("malloc fail");
		return;
	}

	newNode->next = NULL;
	newNode->data = x;

	if (pq->head == NULL)
	{
		assert(pq->tail == NULL);

		pq->head = pq->tail = newNode;
	}
	else
	{
		pq->tail->next = newNode;
		pq->tail = newNode;
	}

	pq->size++;
}

// 队列删除缘元素
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->head);

	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QueueNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
	pq->size--;
}

// 判断队列是否为空
bool QueueEmpty(Queue* pq)
{
	assert(pq);

	return pq->size == 0;
}

// 拿到队头的数据
QDatatype QueueFront(Queue* pq)
{
	assert(pq);

	return pq->head->data;
}

BTNode* BuyTreeNode(BTDataType x)
{
	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	if (newNode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}

	newNode->left = NULL;
	newNode->right = NULL;
	newNode->_data = x;

	return newNode;
}

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	//if (root == NULL)
	//{
	//	printf("NULL\n");
	//	return;
	//}

	//printf("%d => ", root->_data);

	//BinaryTreePrevOrder(root->left);
	//BinaryTreePrevOrder(root->right);
	if (root)
	{
		putchar(root->_data);
		BinaryTreePrevOrder(root->left);
		BinaryTreePrevOrder(root->right);
	}
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	//if (root == NULL)
	//{
	//	printf("NULL\n");
	//	return;
	//}
	//BinaryTreeInOrder(root->left);
	//printf("%d => ", root->_data);
	//BinaryTreeInOrder(root->right);
	if (root)
	{
		BinaryTreeInOrder(root->left);
		putchar(root->_data);
		BinaryTreeInOrder(root->right);
	}
}

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	//if (root == NULL)
	//{
	//	printf("NULL\n");
	//	return;
	//}
	//BinaryTreePostOrder(root->left);
	//BinaryTreePostOrder(root->right);
	//printf("%d => ", root->_data);
	if (root)
	{
		BinaryTreePostOrder(root->left);
		BinaryTreePostOrder(root->right);
		putchar(root->_data);
	}
}



// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue qu;  // 队列 结构体
	BTNode* cur;

	QueueInit(&qu); // 队列的初始化

	QueuePush(&qu, root);  // 队列的 入队
	 
	// 如果队列不为空就 继续循环
	while (!QueueEmpty(&qu))
	{
		cur = QueueFront(&qu);

		putchar(cur->_data);

		if (cur->left)
		{
			QueuePush(&qu, cur->left);
		}

		if (cur->right)
		{
			QueuePush(&qu, cur->right);
		}

		QueuePop(&qu);  // 队列的出队
	}

	QueueDestroy(&qu);   // 队列的 销毁
}