Diffie-Hellman密钥交换协议（Diffie-Hellman Key Exchange，简称DHKE）

news2025/1/11 2:29:58

文章目录

  • Diffie-Hellman密钥交换协议（Diffie-Hellman Key Exchange，简称DHKE）
    • 一、密码学相关的数学基础
      • 1. 素数（质数）
      • 2. 模运算
      • 3. 费马小定理
      • 4. 对数
      • 5. 离散对数
      • 6. 椭圆曲线
        • 常见椭圆曲线
        • 1. NIST系列曲线
          • secp256k1
        • 2. 25519系列曲线
        • 在线生成椭圆曲线
      • 7. 群论
        • 什么是群？
        • 群论的应用
        • 单位元&逆元
        • 交换群、循环群
          • 循环群
          • 交换群（阿贝尔群）
        • 整数加法群
      • 8. 椭圆曲线与数论及群论的关系
    • 二、Diffie-Hellman密钥交换协议（Diffie-Hellman Key Exchange，简称DHKE）
      • 1. 什么是Diffie-Hellman密钥交换协议（DHKE）
      • 2. 单向Diffie-Hellman密钥交换机制 和双向Diffie-Hellman密钥交换机制
      • 3. dh相关漏洞
        • Diffie-Hellman Key Agreement Protocol 资源管理错误漏洞(CVE-2002-20001)
    • 三、ECDH
      • 1. 什么是ECDH
      • 2. 哪些开源项目都在使用ECDH
      • 3. ECDH开源库
      • 4. Ed25519与Curve25519
      • 5. Go语言crypto和golang.org/x/crypto库
        • 演示demo（X25519-DH协议的基本流程,以及如何使用curve25519包实现该协议）
    • 四、参考

Diffie-Hellman密钥交换协议（Diffie-Hellman Key Exchange，简称DHKE）

一、密码学相关的数学基础

1. 素数（质数）

素数一般指质数。质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。比如2、3、5、7、11、13等等都是素数，因为它们只能被1和本身整除。

在这里插入图片描述
素数相乘原理指的是:任何一个大于2的整数都可以唯一分解为素数的乘积。
例如:

  • 24 = 2 * 2 * 2 = 2^3 # 24可以分解为2的幂次
  • 25 = 5 * 5 = 5^2 # 25可以分解为5的幂次
  • 15 = 3 * 5 # 15可以分解为素数3和5的乘积
  • 7是一个素数,只能分解为1 * 7
    根据这个原理,我们可以将任何一个整数分解为素数的乘积。

素数相乘原理的应用场景很广:
整数分解:将一个整数分解为素数的乘积。这在RSA加密算法等应用中很重要。

2. 模运算

模算法是密码学中的核心数学概念。

“模数”(缩写为“mod”)，在拉丁语中是“余数、残数”的意思，表示“取去整体的一部分后剩下的部分”。

例子：
当7除以3时，余数是1。
7 mod 3 = 1 其读成7的3模等于1. 、

给定一个正整数p，任意一个整数n，一定存在等式
n = k p + r n = kp + r n=kp+r 其中k、r是整数，且 0 ≤ r < p，称呼k为n除以p的商，r为n除以p的余数。

在编程语言中,利用%运算符可以很容易求出余数。例如在Python中:

>>> 17 % 5  # 17除以5的余数
2
>>> 25 % 7   # 25除以7的余数 
4
>>> 33 % 11  # 33除以11的余数  
0

模p相等
如果两个数a、b满足a mod p = b mod p，则称他们模p相等，记做
a ≡ b (mod p)
可以证明，此时a、b满足 a = kp + b，其中k是某个整数。
在这里插入图片描述在这里插入图片描述

3. 费马小定理

[推荐]521 同余式 乘法逆元 费马小定理
参考URL: https://www.bilibili.com/video/BV1RD4y1i7PK/
同余（五）——费马小定理
参考URL: https://mp.weixin.qq.com/s?__biz=MzI2NjEyMTg3Mw==
最美数学系列-什么是费马小定理以及如何证明它？
参考URL: https://www.bilibili.com/video/BV14A411h7oD/
初等数论入门：什么是“域”
参考URL: https://www.toutiao.com/article/6860442610624889348/
【有趣的数学】E02——费马小定理，判别素数的方法？
参考URL: https://www.bilibili.com/video/BV1mM4y1A7FR/
[推荐]数论：费马小定理
参考URL: https://www.bilibili.com/video/BV1RG41137tR/

费马小定理是数论中的一个重要定理,由费马在17世纪（在1636年提出）提出。它阐明了整数在模素数下的乘法性质,是构建RSA算法等密码学系统的理论基础。

费马小定理：

如果p是一个质数，而整数a不是p的倍数，则有a^（p-1）≡1（mod p）
如果整数a与素数p互质,那么a的(p-1)次方在模p下等于1。

我们知道，当 p 为素数且用 (mod p) 进行分类时，费马小定理是成立的。

也就是说，对于非 0 的 a 而言，以下同余式恒成立。

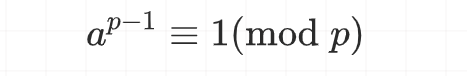在这里插入图片描述在此令 a ( p − 1 ) = a ⋅ a ( p − 2 ) a^( p-1)=a·a^(p-2) a(p−1)=a⋅a(p−2)，则
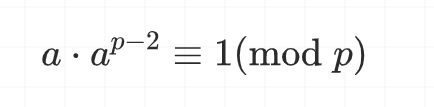
在这里插入图片描述
由此可知，a^(p-2) 是 a 的逆元。

因此，非 0 的 a 确实总是存在逆元。由此可知，相应的剩余类可以构成域。例如 (mod 5)
在这里插入图片描述

4. 对数

对数符号log出自拉丁文logarithm，最早由意大利数学家卡瓦列里（Cavalieri）所使用。20世纪初，形成了对数的现代表示。为了使用方便，人们逐渐把以10为底的常用对数及以无理数e为底的自然对数分别记作lgN和lnN。

如果a的x次方等于N（a>0，且a≠1），那么数x叫做以a为底N的对数（logarithm），记作
x = l o g a N x=log_aN x=loga​N。其中，a叫做对数的底数，N叫做真数。
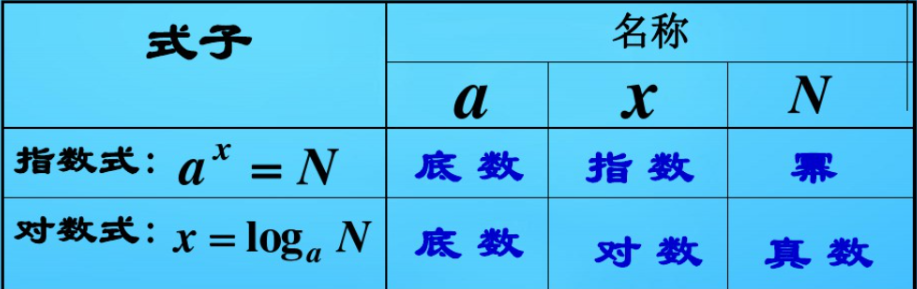
在这里插入图片描述
在指数式中，x就是指数。在对数式中，x就是对数。

在这里插入图片描述

5. 离散对数

【离散对数】离散对数的性质
参考URL: https://www.bilibili.com/video/BV1hY411D7Bv/
离散对数
参考URL: https://www.bilibili.com/video/BV1TJ411a7x6/
离散数学（国家级）-北京大学
参考URL: https://www.bilibili.com/video/BV1V7411t7HL/
[推荐]图解 ECDHE 密钥交换算法
参考URL: https://www.toutiao.com/article/6920920871188120068/

离散对数是在对数运算的基础上加了「模运算」，也就说取余数，对应编程语言的操作符是「%」，也可以用 mod 表示。离散对数的概念如下图：

在这里插入图片描述上图的，底数 a 和模数 p 是离散对数的公共参数，也就说是公开的，b 是真数，i 是对数。知道了对数，就可以用上面的公式计算出真数。但反过来，知道真数却很难推算出对数。

特别是当模数 p 是一个很大的质数，即使知道底数 a 和真数 b ，在现有的计算机的计算水平是几乎无法算出离散对数的，这就是 DH 算法的数学基础。

离散对数公钥加密算法是目前最为热门的公钥加密算法 ，其安全性要远远高于基于大数分解的RSA算法。离散对数在许多数论与密码学问题中有重要应用,例如Diffie-Hellman密钥交换协议和ElGamal加密算法等都依赖离散对数。

6. 椭圆曲线

[推荐]ECC椭圆曲线加密算法原理
参考URL: https://blog.csdn.net/liangjisheng/article/details/79428639
公钥加密技术ECC椭圆曲线加密算法原理
参考URL: https://www.bilibili.com/video/BV1BY411M74G
椭圆曲线数字签名算法（一）
参考URL: https://www.bilibili.com/video/BV1eS4y1t7Jy/
【ECC加密算法】| ECC加密原理详解| 椭圆曲线加密| 密码学| 信息安全
参考URL: https://www.bilibili.com/video/BV1v44y1b7Fd/
椭圆曲线加密与哈希函数是什么？非对称加密是什么？比特币中的数学原理
参考URL: https://www.bilibili.com/video/BV1TE411q7mW/
[推荐]【Computerphile计算机系列】椭圆曲线和密码算法（合集见视频列表）
参考URL: https://www.bilibili.com/video/BV1q34y197Zq/
[清晰，强烈推荐]徐伟光：椭圆曲线密码学（四电老陈）
参考URL: https://www.bilibili.com/video/BV1ZT411k7z8/

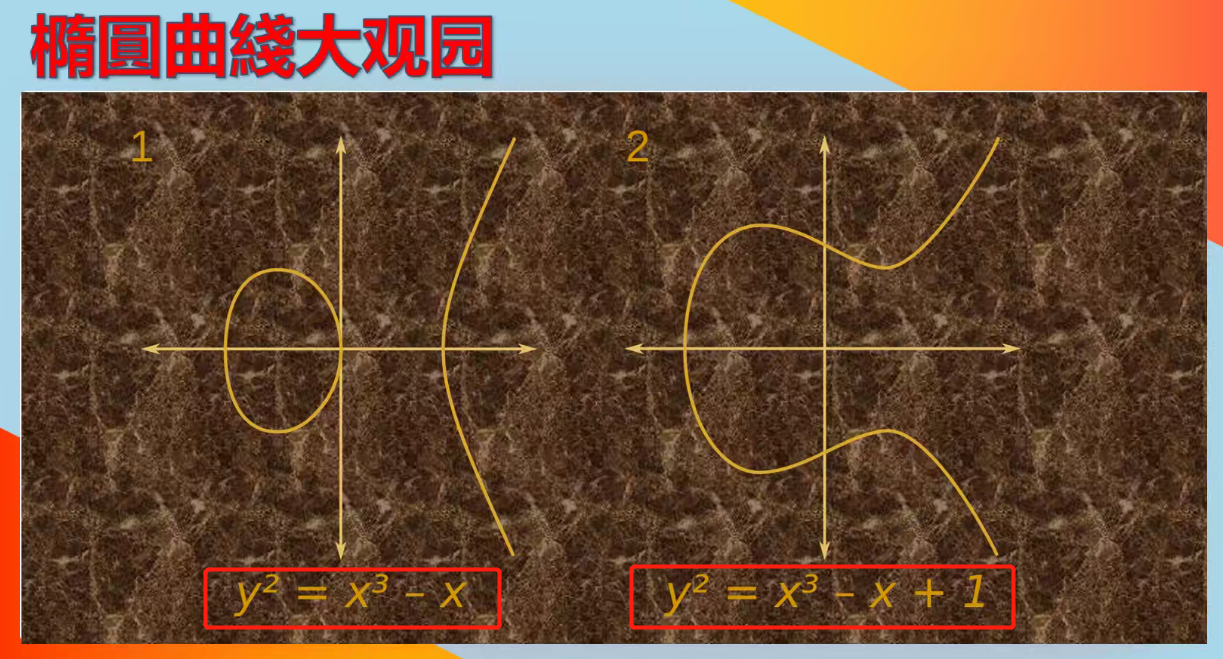
在这里插入图片描述在这里插入图片描述
上图，来自由陆晨博士主讲的「高效密码运算算法」,如有侵权，联系删除~

椭圆曲线加密法（ECC）是一种公钥加密技术，以椭圆曲线理论为基础，在创建密钥时可做到更快、更小，并且更有效。ECC 利用椭圆曲线等式的性质来产生密钥，而不是采用传统的方法利用大质数的积来产生。

ECC所谓的椭圆曲线在数学上就是一个数学方程式，该方程式对应一个椭圆曲线(并不是椭圆)，该曲线上的点由方程式决定。

最常见的韦尔斯特拉斯（Weierstrass）方程:
y 2 = x 3 + a x + b y^2 = x^3 + ax + b y2=x3+ax+b 这里a和b是实数,并满足 4 a 3 + 27 b 2 ! = 0 4a^3 + 27b^2 != 0 4a3+27b2!=0。

4 a 3 + 27 b 2 ! = 0 4a^3+27b^2!=0 4a3+27b2!=0这个限定条件是为了保证曲线不包含奇点(singularities) 所谓奇点就是不可导的点。

在椭圆曲线密码学中,椭圆曲线上定义了一个点加法运算。为了使这个运算符满足阿贝尔群的性质,椭圆曲线上的所有点都必须参与运算。这就要求椭圆曲线上的每一个点,都必须可以与其他任意点相加。
但是,椭圆曲线上存在一类特殊点,这类点的加法运算无法定义,它们就是所谓的“奇点”或“不可导点”。这是因为,当我们尝试连接这些点和其他点时,会得到一个垂直于椭圆曲线的直线,这条直线与椭圆曲线的交点个数可能是1个或3个,而不是标准的2个交点。

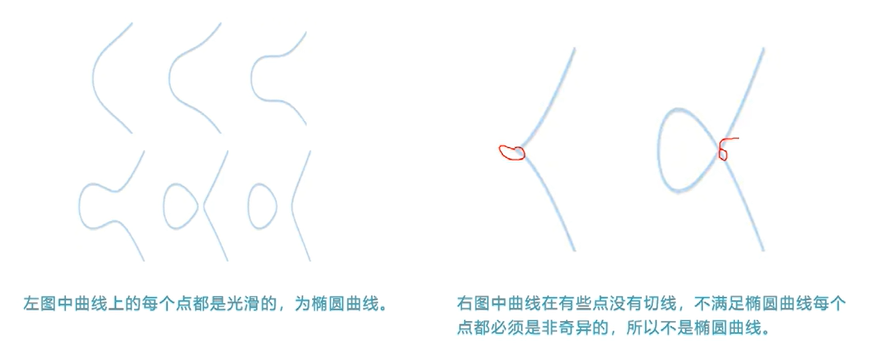
在这里插入图片描述

  1. 椭圆曲线上的点满足一种特殊的加法运算,这种加法运算使其形成一个阿贝尔群。这是椭圆曲线最重要的性质,在密码学中有重要应用。
  2. 椭圆曲线上的离散对数问题也是一个难解问题,这为椭圆曲线密码体制提供了安全性保证。

椭圆曲线在现代密码学中有着广泛的应用,像ECDSA、EdDSA等数字签名算法,以及ECC加密算法都基于椭圆曲线。椭圆曲线密码体制的安全性依赖于椭圆曲线难以解析的几何结构和难以求解的离散对数问题。

常见椭圆曲线

两大系列

1. NIST系列曲线

美国国家标准与技术研究院（National Institute of Standards and Technology, NIST）
目前广泛使用
代表: secp256k1
Secp256k1是指比特币中使用的ECDSA(椭圆曲线数字签名算法)曲线的参数。

spec256k1、spec256r1都属于椭圆曲线数字签名算法ECDSA(Elliptic Curve Digital Signature Algorithm)签名的具体实现，只是椭圆曲线函数不同。是由 NIST(National Institute of Standards and Technology)这个组织确定的。

下图是各加密货币采用的签名算法的现状，多数是spec256k1。
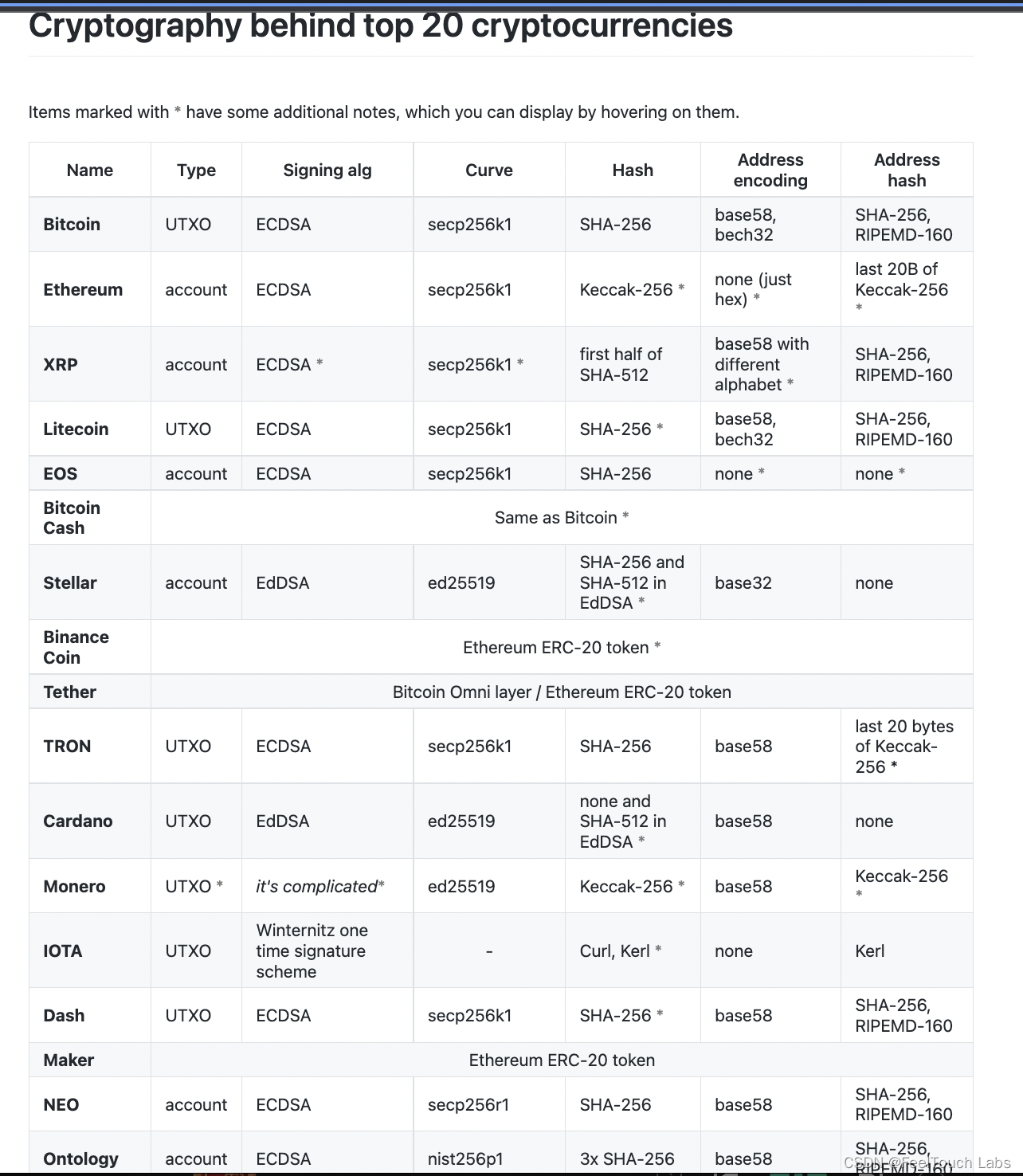在这里插入图片描述secp256k1 是区块链项目中应用最多的椭圆曲线算法，源于比特币中的应用，后来的大多数区块链项目如以太坊等都在用。

secp256k1

SEC是一个椭圆曲线的标准,一些常用的曲线,如secp256k1、secp256r1都是这个标准下的，在高效密码学标准(Certicom Research,http://www.secg.org/sec2-v2.pdf)中进行了定义。

名称中的前三个字母sec代表Standards for Efficient Cryptography (SEC)，后面的p256K1指的是参数256位素数域。Secp256k1为基于Fp有限域（又名伽罗瓦域）上的椭圆曲线，由于其特殊构造的特殊性，其优化后的实现比其他曲线性能上可以特高30％，有明显以下两个优点：

1）占用很少的带宽和存储资源，密钥的长度很短。 2）让所有的用户都可以使用同样的操作完成域运算。

椭圆曲线图 y 2 = x 3 + 7 y ^ 2 = x ^ 3 + 7 y2=x3+7
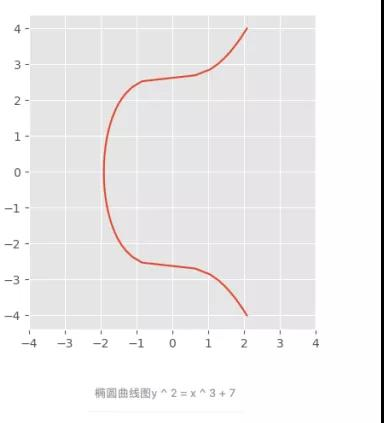
在这里插入图片描述

在平面中的椭圆曲线上的加法在几何上根据线截取曲线的位置来定义。我们不会在这里讨论几何，除了说它归结为一组涉及实数的方程。但我们并没有在实数域上去工作，而是在有限域。有限域p，其中

p = 2^256 - 2^32 - 977

这里选择p相对接近 2 256 2^{256} 2256。它不是小于 2 256 2^{256} 2256的最大素数; p和 2 256 2^{256} 2256之间有很多素数。其他因素也同样影响着选择p。请注意，我们不是在整数mod p本身工作，而是在一个阿贝尔群中，其加法法则由整数mod p上的椭圆曲线定义 。

2. 25519系列曲线

著名密码学家Daniel J. Bernstein在2006年独立设计的椭圆曲线加密/签名/密钥交换算法
目前最快
代表: ed25519

Curve25519/Ed25519/X25519 是著名密码学家Daniel J. Bernstein在2006年独立设计的椭圆曲线加密/签名/密钥交换算法，与现有的任何椭圆曲线算法完全独立，其中Ed25519用于签名。

25519系列曲线自2006年发表以来，除了学术界无人问津，2013年爱德华·斯诺登曝光棱镜计划后，该算法突然大火，OpenSSH迅速增加了对25519系列的支持，RFC增加了SSL/TLS对X25519密钥交换协议的支持。

RFC 7748为椭圆曲线密码学定义了一套标准,它指定了几条主要的安全椭圆曲线以及相关参数,这有助于算法和协议的统一和互操作。

RFC 7748 定义了9条不同的椭圆曲线,以及每条曲线对应的Hash函数。具体如下:

曲线名称abpHash函数安全级别
Curve2551948666212^255 - 19SHA-512/256128 bit
Curve44815632612^448 - 2^224 - 1SHAKE256(512)224 bit
Curve571353805404112^571 - 1SHA-512/256233 bit
Curve1417397077115312^1417 - 1SHA-512/256379 bit
Edwards255191-390812^255 - 39SHA-512/256128 bit
EdKohel20012^251 + 10003444968317156028688767991075998066036788681627368077Shake256(512)127 bit
Wei2551920x51a6b50x3ffffffSHA-512/25677 bit
Wei4480x4d323f0x1f8b370x7fffffffbffSHAKE256(512)224 bit
Wei448.10x291f70x378a90x7fffffffbff7SHAKE256(512)224 bit

Curve25519由著名的密码学家BERNSTEIN教授于2005 年提出用，在2013 年开始广泛运用。2016年，IETF发布了RFC 7748，推荐使用 Curve25519 和Curve448。

最重要和应用最广泛的两条曲线是:

  • Curve25519:用于ECDH密钥交换和EdDSA签名,128位安全级别。
  • Curve448:用于ECDH密钥交换,224位安全级别。
    其他曲线目前应用相对较少。

2014年OpenSSH 默认使用基于 Curve25519的ECDH算法
OpenSSL从1.1.0版本7开始支持 Curve25519.

在线生成椭圆曲线

在线生成椭圆曲线: https://www.desmos.com/calculator/ialhd71we3

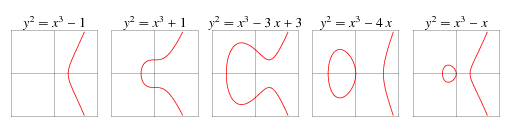
在这里插入图片描述

7. 群论

[推荐]五次方程（三）群论入门 隐藏在根与系数关系中的秘密
参考URL: https://www.bilibili.com/video/BV1Wb41187wA/
[推荐，讲的很好]【什么是群】代数结构、群的概念，如何判断一个代数结构是群，尽在其中
参考URL: https://www.bilibili.com/video/BV1WG4y147vd

什么是群？

群论（Group Theory）是数学的一个分支，研究抽象代数结构中的群的性质。
群是一个包含一组元素和一个二元运算（通常称为“乘法”）的代数结构。这个运算满足以下四个基本性质：

  • 封闭性（Closure）：对于群中任意两个元素a和b，它们的乘积a*b也属于群。

  • 结合律（Associativity）：对于群中任意三个元素a、b和c，满足 (ab)c = a(bc)。

  • 单位元（Identity）：存在一个特殊的元素e（也称为“单位元”或“恒等元”），使得对于群中任意元素a，满足 ea = ae = a。

  • 逆元（Inverses）：对于群中的每一个元素a，都存在一个元素a’（称为“逆元”），满足 a*a’ = a’*a = e，其中e是单位元。

群论的应用

群论在数学、物理和计算机科学等领域有着广泛的应用。

在数学中，群论可以用来研究对称性、几何变换和代数方程的解。
在物理学中，它被用来描述粒子和宇宙间的对称关系，如晶体结构和量子力学等。
在计算机科学中，群论可以应用于密码学、编码理论和图论等领域。

DH密钥交换算法基于数学中的群论。

单位元&逆元

定理1： 群里的单位元是唯一的。
定理2： 每个元素只有唯一的逆元。

交换群、循环群

循环群

循环群是指可以由单个元素生成的群。这意味着群中的所有元素都可以通过这个生成元（或其逆元）的幂运算得到。形式上，对于群G中的某个元素g，如果G中的所有元素都可以表示为g^n的形式（n是整数），那么我们称G是由g生成的循环群，记作G= 。

有限循环群：模n加法群是一个典型的有限循环群，它包含n个元素{0, 1, 2, …, n-1}，群运算是模n加法。例如，模4加法群中的元素可以表示为{0, 1, 2, 3}，由生成元1生成。

循环群可以是有限的也可以是无限的。

无限循环群：整数加法群是一个典型的无限循环群，它包含整数集合，群运算是整数加法。整数加法群可以看作是由生成元1（或-1）生成的无限循环群。

循环群具有简单的结构，使得它们在理论研究和实际应用中具有优势。此外，循环群总是交换的，即满足交换律。

交换群（阿贝尔群）

交换群（也称阿贝尔群）是满足交换律的群，即对于群中任意两个元素a和b，有ab = ba。交换群在群论中具有重要地位，因为许多实际应用和理论研究都涉及交换性质。

以下是一些交换群的例子：

模n加法群：前面提到的模n加法群是一个典型的有限交换群。模n加法群的群运算是模n加法，它具有交换性。

整数加法群：整数加法群是一个无限交换群，它包含整数集合，群运算是整数加法。

实数加法群：实数加法群是一个无限交换群，它包含实数集合，群运算是实数加法。

有理数乘法群：有理数乘法群是一个无限交换换群，它包含非零有理数集合，群运算是有理数乘法。这个群具有交换性，因为有理数乘法满足交换律。

交换群（阿贝尔群）在代数和其他数学领域具有重要应用。许多代数结构（如向量空间、模等）可以看作是基于交换群的扩展。此外，在代数几何、代数拓扑和数论等领域，交换群也起着关键作用。例如，在代数拓扑中，基本群是用于刻画拓扑空间的连通性质的一个重要不变量，而在许多情况下，基本群是一个交换群。

在数论中，有理数乘法群和椭圆曲线上的点构成的群等结构都与交换群密切相关。

整数加法群

在这里插入图片描述
整数加法群(additive group of integers)亦称整数加群，是一种具体的群，指全体整数在通常的加法运算下所成的群，常用Z表示整数加法群。

Zm表示在模m下的加法群是一个常用的表示法,离散对数就是定义在这些有限群上的函数。

例1:在整数模7的加法群Z7={0,1,2,3,4,5,6}上,定义底数为3的离散对数函数log3:Z7→N。

Z7是一个有限(元素个数有限)Abel群（,即可以定义加法和乘法,并且满足封闭性、结合性、存在幺元等群的性质）,包含7个元素{0,1,2,3,4,5,6}, **加法运算在模7下进行，所以在这个群上任意两个元素之和仍在该群中。**这形成一个循环群,每个元素都是前一个元素的7倍。

8. 椭圆曲线与数论及群论的关系

巨大的数学谜团——椭圆曲线，代数、几何和数论的完美结合
参考URL: https://www.toutiao.com/article/7193707494140117515/
密码学系列 - 椭圆曲线 ECC - ED25519
参考URL: https://blog.csdn.net/wcc19840827/article/details/104621378/

**椭圆曲线的是一场数论、抽象代数和几何之间的美丽舞蹈。**椭圆曲线也可以看成是加法群。

椭圆曲线的神奇之处在于，我们可以在椭圆曲线上的有理数点（也就是说，x和y坐标都是有理数）之间定义一个运算（称它为“⊕”），这样曲线上这些点的集合就变成了一个关于运算“⊕”和单位元素（无穷远处的点）的阿贝尔群。

那么 y 2 = f ( x ) y^2= f(x) y2=f(x)描述的是一条椭圆曲线，除了“无穷远点”（即椭圆曲线上点在加法运算下构成的群中的单位元）。

让我们定义这个运算。如果你在曲线上取两个有理点（例如P和Q），并考虑一条经过它们的直线，那么这条直线与曲线相交于另一个有理点（可能是无穷远处的点）。我们称这个点为-R。

现在，因为曲线是关于x轴对称的，我们得到另一个有理点R。

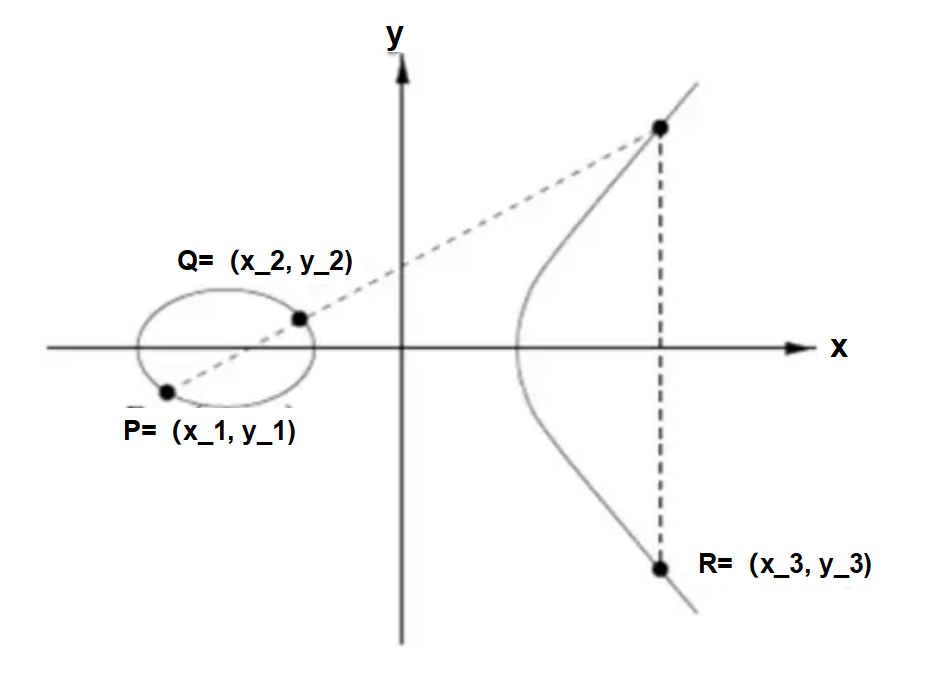在这里插入图片描述这个反射点（上图中的R）是前面提到的两个点（P和Q）的相加。我们可以写成 :
P ⊕ Q = R P⊕Q=R P⊕Q=R

可以证明，这个运算是满足结合律，这真的很令人惊讶。此外，无穷远处的点作为这个运算的（唯一）恒等式，每个点都有一个逆点。

基于椭圆曲线的群定义

特性

  • 封闭性：因为椭圆曲线上的点相加，还是椭圆曲线上的点。
  • 结合律：P+(Q+R) = (P+Q)+R = 0
  • 单位元: 单位元是0, 即 P+0 = P
  • 逆元: 一个椭圆曲线上的点P的逆元，是相对x坐标的对称点
  • 交换律：P+Q = Q+P

椭圆曲线上的点运算和普通实数域上的运算有很大差别,当前尚未存在一种有效的算法对椭圆曲线离散对数问题进行破译。

标量乘法
nP = P + P + P + … +P

找到生成点G的倍数kG。也就是G相加k次
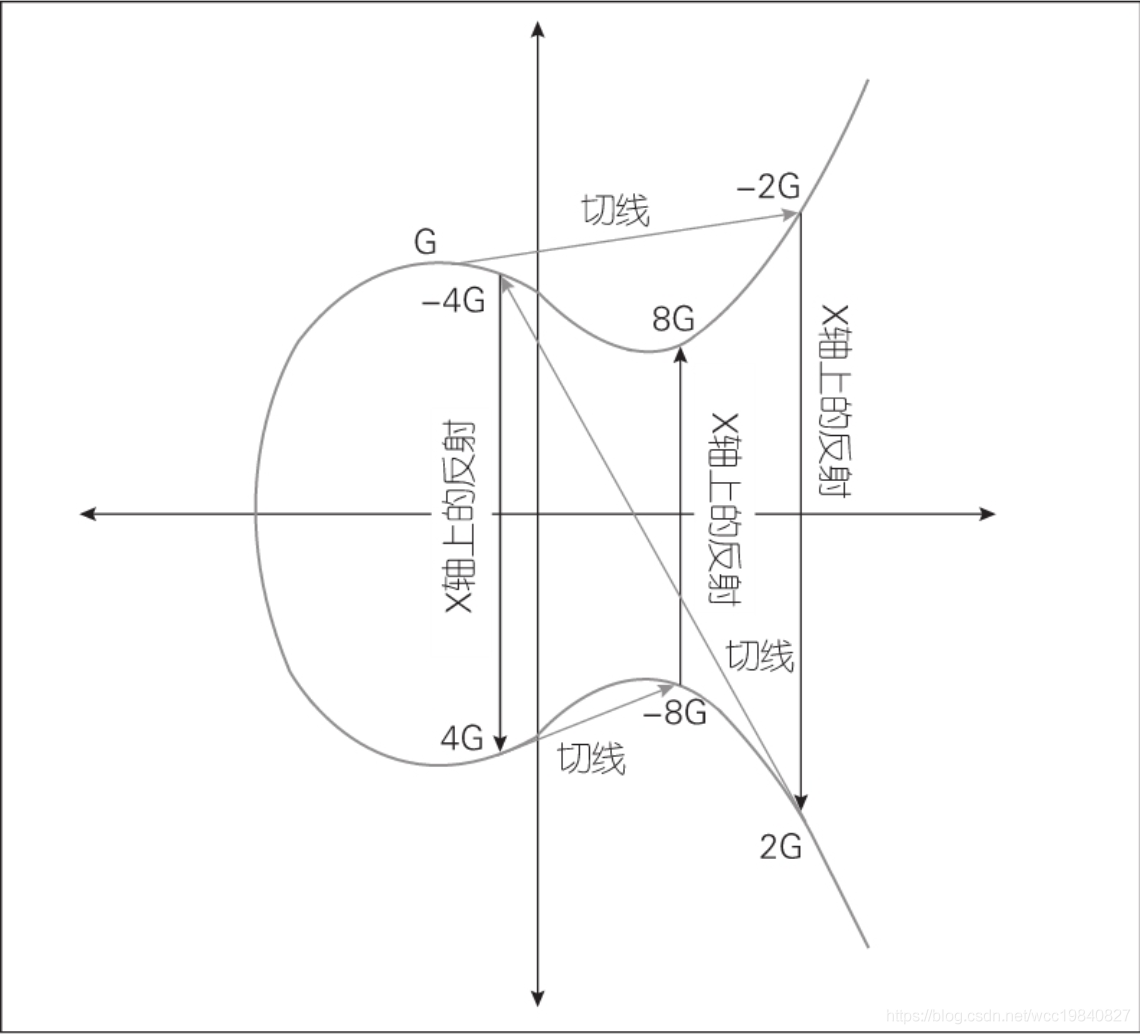
在这里插入图片描述
请大家注意，前面学到的椭圆曲线是连续的，并不适合用于加密；所以，我们必须把椭圆曲线变成离散的点。

让我们想一想，为什么椭圆曲线为什么连续？是因为椭圆曲线上点的坐标，是实数的（也就是说前面讲到的椭圆曲线是定义在实数域上的），实数是连续的，导致了曲线的连续。因此，我们要把椭圆曲线定义在有限域上（顾名思义，有限域是一种只有由有限个元素组成的域）。

域的概念是从我们的有理数，实数的运算中抽象出来的。简单的说，域中的元素同有理数一样，有自己得加法、乘法、除法、单位元(1)，零元(0),并满足交换率、分配率。

下面，我们给出一个有限域Fp，这个域只有有限个元素。

Fp中只有p（p为素数）个元素0,1,2 …… p-2,p-1；
　　Fp 的加法（a+b）法则是 a+b≡c (mod p)；即，(a+c)÷p的余数 和c÷p的余数相同。
　　Fp 的乘法(a×b)法则是 a×b≡c (mod p)；
　　Fp 的除法(a÷b)法则是 a/b≡c (mod p)；即 a×b-1≡c (mod p)；（b-1也是一个0到p-1之间的整数，但满足b×b-1≡1 (mod p)；具体求法可以参考初等数论，或我的另一篇文章）。
　　Fp 的单位元是1，零元是 0。

同时，并不是所有的椭圆曲线都适合加密。y2=x3+ax+b是一类可以用来加密的椭圆曲线，也是最为简单的一类。下面我们就把y2=x3+ax+b 这条曲线定义在Fp上：

选择两个满足下列条件的小于p(p为素数)的非负整数a、b
　　4a3+27b2≠0　(mod p)
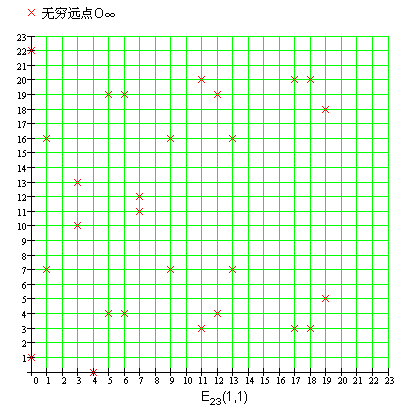
　　则满足下列方程的所有点(x,y)，再加上 无穷远点O∞ ，构成一条椭圆曲线。
　　y2=x3+ax+b (mod p)
　　其中 x,y属于0到p-1间的整数，并将这条椭圆曲线记为Ep(a,b)。

我们看一下y2=x3+x+1 (mod 23)的图像

在这里插入图片描述
椭圆曲线在不同的数域中会呈现出不同的样子，但其本质仍是一条椭圆曲线。

二、Diffie-Hellman密钥交换协议（Diffie-Hellman Key Exchange，简称DHKE）

1. 什么是Diffie-Hellman密钥交换协议（DHKE）

[推荐]DH 算法
参考URL: https://xiaolincoding.com/network/2_http/https_ecdhe.html#dh-%E7%AE%97%E6%B3%95

DHKE是一种通过公共通道安全地交换加密密钥的数学方法，以Whitfield Diffie和Martin Hellman的名字命名。DH是密码学领域中最早实现的公钥交换实例之一。这两位也是大名鼎鼎的文章《密码学的新方向》的作者。

Deffie-Hellman(简称 DH) 密钥交换是最早的密钥交换算法之一，它使得通信的双方能在非安全的信道中安全的交换密钥，用于加密后续的通信消息。 Whitfield Diffie 和 Martin Hellman 于 1976 提出该算法，之后被应用于安全领域，比如 Https 协议的 TSL(Transport Layer Security)以 DH 算法作为密钥交换算法。

由于DHKE本身不提供通信双方的身份验证。因此，DHKE容易受到中间人攻击（man-in-the-middle attack）。
x = l o g 2 y x = log_2y x=log2​y

上述公式其中x为对数，y为真数，底为2。对于上述例子，32的对数是5，64的对数是6，可以看出对数的取值是能够连续的。

但是离散对数的取值是无法连续，离散也是因此得名。
a i ( m o d p ) = b a^i (mod p ) = b ai(modp)=b

对于一个整数b和一个质数p的一个原根a，能够找到唯一一个指数i使得上述公式成立，那么指数i称为b的以a为底数的模p的离散对数。

底数a和和模p是离散对数的公开参数，b是真数，i是对数，知道了对数i我们很轻松就能算出真数b，但是如果知道真数b但是很难计算对数i，尤其是模p很大的时候，现有的计算机的计算能力是无法破解的。

2. 单向Diffie-Hellman密钥交换机制 和双向Diffie-Hellman密钥交换机制

Diffie-Hellman密钥交换是一种通信协议，用于在不安全的通信渠道上协商密钥。单向Diffie-Hellman密钥交换机制只允许一个方向的密钥交换，常见于客户端和服务器之间的通信。这种协议仅使用了一个方向的公钥加密算法来保证密钥安全，因此可能存在中间人攻击。

单向Diffie-Hellman密钥交换：

            Client                                Server
              |                                      |
          发送公钥A                              接收公钥A
              |                                      |
          计算共享密钥K                           计算共享密钥K
              |                                      |
              |                                      |
          发送加密数据                             接收加密数据

static DH 算法里有一方的私钥是静态的，也就说每次密钥协商的时候有一方的私钥都是一样的，一般是服务器方固定，即 a 不变，客户端的私钥则是随机生成的。

于是，DH 交换密钥时就只有客户端的公钥是变化，而服务端公钥是不变的，那么随着时间延长，黑客就会截获海量的密钥协商过程的数据，因为密钥协商的过程有些数据是公开的，黑客就可以依据这些数据暴力破解出服务器的私钥，然后就可以计算出会话密钥了，于是之前截获的加密数据会被破解，所以 static DH 算法不具备前向安全性。

双向Diffie-Hellman密钥交换机制允许双方通过互相交换公钥来生成对称密钥。该协议可以防止中间人攻击，因为双方都要互相验证对方的公钥。具体实现方法是，在每次交换之前，双方都会验证对方的公钥是否合法，并且使用数字签名和哈希函数对其进行认证。

双向Diffie-Hellman密钥交换：

            Client                                Server
              |                                      |
          发送公钥A                              接收公钥A
          发送认证信息                            接收认证信息
              |                                      |
     验证对方公钥合法性                      验证对方公钥合法性
              |                                      |
       使用哈希函数生成                   使用哈希函数生成
        共享密钥K的签名                       共享密钥K的签名
              |                                      |
          发送签名                              接收签名
              |                                      |
     验证对方签名合法性                      验证对方签名合法性
              |                                      |
          计算共享密钥K                           计算共享密钥K
              |                                      |
              |                                      |
          发送加密数据                             接收加密数据

双向Diffie-Hellman密钥交换机制比单向Diffie-Hellman密钥交换更安全，因为它包含了更多的验证和认证过程。但是，由于增加了额外的计算和通信开销，双向Diffie-Hellman密钥交换可能会降低传输速度。

既然固定一方的私钥有被破解的风险，那么干脆就让双方的私钥在每次密钥交换通信时，都是随机生成的、临时的，这个方式也就是 DHE 算法，E 全称是 ephemeral（临时性的）。

所以，即使有个牛逼的黑客破解了某一次通信过程的私钥，其他通信过程的私钥仍然是安全的，因为每个通信过程的私钥都是没有任何关系的，都是独立的，这样就保证了「前向安全」。

3. dh相关漏洞

Diffie-Hellman Key Agreement Protocol 资源管理错误漏洞(CVE-2002-20001)

POC地址：https://github.com/c0r0n3r/dheater
D(HE)ater是攻击（CVE-2002-20001）的D(HE)ater概念实现的证明，可以通过执行Diffie-Hellman钥匙交换来执行拒绝服务。

由于低版本的OpenSSH使用了过时不安全的加密算法协议，通常OpenSSH在版本迭代更新时会弃用这些不安全的加密算法。
如果我们仍要继续使用旧版本的OpenSSH，可以根据实际情况，考虑屏蔽掉不安全的加密算法，以降低安全风险。

查看客户端支持的kexalgorithms

ssh -Q kex

查看服务端支持的kexalgorithms

sshd -T | grep -w kexalgorithms

修复方法
修改sshd_config配置文件，屏蔽掉不安全的KexAlgorithms。

CVE-2002-20001是 affect SSH的一个安全漏洞,允许未经鉴权的用户绕过某些SSH服务端的访问控制。这个漏洞影响使用以下Diffie-Hellman组密钥交换算法的SSH连接:

Diffie-Hellman key exchange algorithms can be removed by setting the KexAlgorithms configuration option.

KexAlgorithms -diffie-hellman-group1-sha1,diffie-hellman-group1-sha256,diffie-hellman-group14-sha1,diffie-hellman-group14-sha256,diffie-hellman-group15-sha256,diffie-hellman-group15-sha512,diffie-hellman-group16-sha256,diffie-hellman-group16-sha512,diffie-hellman-group17-sha512,diffie-hellman-group18-sha512,diffie-hellman-group-exchange-sha1,diffie-hellman-group-exchange-sha256,diffie-hellman-group-exchange-sha512

为了防范这个漏洞,您应该在SSH服务端(sshd)中屏蔽上述算法。

编辑sshd配置文件/etc/ssh/sshd_config,添加如下配置:

KexAlgorithms ecdh-sha2-nistp256,ecdh-sha2-nistp384,ecdh-sha2-nistp521,curve25519-sha256

这将只保留ecdh-sha2-nistp256,ecdh-sha2-nistp384,ecdh-sha2-nistp521,curve25519-sha256 算法,并屏蔽基于Diffie-Hellman的密钥交换算法,进而防范CVE-2002-20001漏洞。

验证漏洞是否存在

  1. 客户端远程时强制指定ssh使用的密钥交换算法
ssh -v -oKexAlgorithms=diffie-hellman-group1-sha1 root@192.168.0.223
  1. 不指定 KexAlgorithms 连接测试
ssh -v root@192.168.0.223

三、ECDH

1. 什么是ECDH

Diffie-Hellman(DH)密钥交换是一种在非保护信道中建立共享密钥的方法，是很多安全协议的基础。而相比传统基于有限域的DH算法，基于椭圆曲线密码学(EIliptic Curve Cryptography,ECCL)的ECDH(Elliptic Curve
Diffie-Hellman)密钥交换由于其性能优势，目前更受产业界青睐并逐步推广。

ECDH(Elliptic Curve Diffie-Hellman)是一种基于椭圆曲线的密钥交换协议,用于建立彼此之间的共享密钥,以用于后续加密通信。

elliptic
美: [ɪ’lɪptɪk]
英: [ɪ’lɪptɪk]
adj. 椭圆(形)的；省略法的；有省略处的
网络 椭圆的；椭圆形的；省略的

curve
美: [kɜrv]
英: [kɜː®v]
n. 曲线；弯曲；曲面；弧线
v. （使）沿曲线移动；呈曲线形
网络 弯道；曲球；使弯曲

ECDH 密钥协商算法是 DH 算法演进过来的，所以我们先从 DH 算法说起。
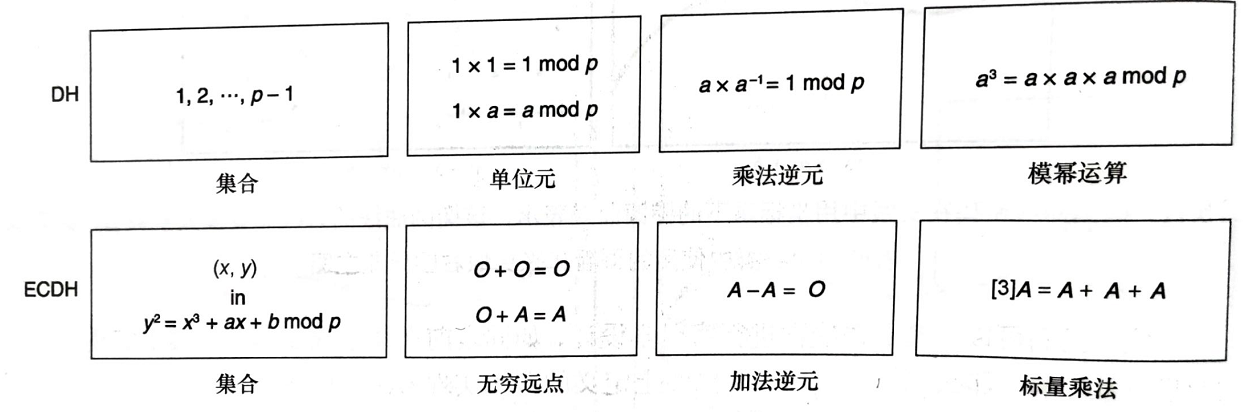
在这里插入图片描述

DH 算法是非对称加密算法， 因此它可以用于密钥交换，该算法的核心数学思想是离散对数。

ECC算法和DH结合使用，用于密钥磋商，这个密钥交换算法称为ECDH。 交换双方可以在不共享任何秘密的情况下协商出一个密钥。ECC是建立在基于椭圆曲线的离散对数问题上的密码体制，给定椭圆曲线上的一个点P，一个整数k，求解Q=kP很容易；给定一个点P、Q，知道Q=kP，求整数k确是一个难题。

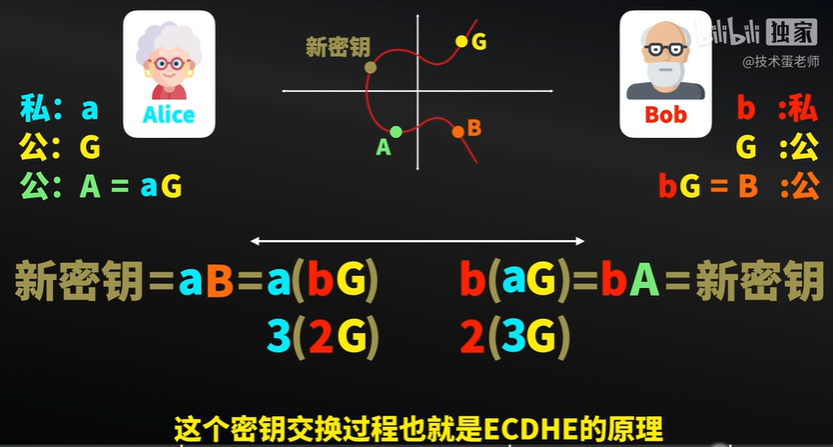在这里插入图片描述Alice 公钥计算 aG=A
Bob 公钥计算 bG=B

Alice可以根据 Bob的公钥以及自身的私a算共享秘钥： [a]B

Bob根据Alice的公钥以及自身的私钥a算共享密钥： [b]A

双方最终计算出相同的结果:[a]B=[a][b]G=[ab]G=[b][a]G=[b]A

2. 哪些开源项目都在使用ECDH

  1. TLS:
    TLS1.3版本开始支持ECDH作为密钥交换机制,主流开源TLS库如GnuTLS、BoringSSL等都实现了ECDH支持。

  2. OpenSSH
    OpenSSH支持ECDH密钥交换算法,用于SSH通信建立共享密钥。

  3. WireGuard
    WireGuard是一款新型VPN技术,WireGuard 使用的交换密钥算法是ECDH，它是DH算法的一个变种，即协商安全信道的双方，持有一个私密的随机数，然后交换公开的随机数，通过同余算法两端独立计算出相同的密钥。

  4. libgcrypt:
    libgcrypt是GNU工具箱中的一个加密算法库,其中就实现了ECDH算法。许多基于libgcrypt的软件都可以使用ECDH。

3. ECDH开源库

ECDH开源库的GitHub地址:

  1. OpenSSL:
    https://github.com/openssl/openssl

  2. Cryptopp:
    https://github.com/weidai11/cryptopp

  3. libsodium:
    https://github.com/jedisct1/libsodium
    广泛应用的C/C++密码库

  4. libgcrypt:
    https://github.com/gpg/libgcrypt

  5. mbed TLS(前PolarSSL):
    https://github.com/ARMmbed/mbedtls

  6. RELIC:
    https://github.com/relic-toolkit/relic

  7. Charm Crypto:
    https://github.com/JHUISI/charm

  8. libtomcrypt:
    https://github.com/libtom/libtomcrypt
    除上述开源库外,Bouncy Castle的GitHub地址是:
    https://github.com/bcgit/bc-csharp
    Java中的ECDH实现位于JCE(Java Cryptography Extension)标准库中,部分Java开源库也有自己的实现。

4. Ed25519与Curve25519

在密码学中，Curve25519是一种椭圆曲线，被设计用于椭圆曲线迪菲-赫尔曼（ECDH）密钥交换方法，可用作提供256比特的安全密钥。它是不被任何已知专利覆盖的最快ECC曲线之一。

最初的Curve25519草稿将其定义成一个迪菲-赫尔曼（DH）函数。在那之后Daniel J. Bernstein提出Curve25519应被作为底层曲线的名称，而将X25519作为其DH函数的名称。

Ed25519 和 Curve25519 实际上使用的是同一条椭圆曲线 - Curve25519

Ed25519:

  • 是一种签名算法(用于生成和验证数字签名)。它可以用来验证消息的来源和完整性。
  • 使用椭圆曲线加密算法 Curve25519 生成密钥对。
  • 由 Daniel J. Bernstein （简写DJB） 设计,2011 年提出。

Curve25519:

  • 是一种密钥交换协议。它允许两方生成一个共享的秘密密钥,该密钥可以用在对称加密算法中。
  • 由 DJB 设计,2006 年提出。

5. Go语言crypto和golang.org/x/crypto库

crypto和golang.org/x/crypto都是Go语言标准库中的包，但它们的作用领域略有不同。

crypto包提供了常用的加密算法、哈希函数、数字签名等功能。这些函数已经过广泛测试和验证，并且被认为是安全可靠的。crypto包是Go语言标准库的一部分，因此可以直接使用，而无需额外安装其他依赖项。

**golang.org/x/crypto包则是Go语言实现的一些密码学算法的扩展库。**这个包包含了一些在标准库之外的加密算法、哈希函数、数字签名等功能，例如bcrypt、chacha20、poly1305等。这些算法可能还没有经过如标准库所提供的那样广泛的测试和验证，但它们被认为是安全可靠的，并且在许多项目中得到了广泛使用。由于这个包并不是标准库的一部分，因此需要单独安装。

综上所述，crypto和golang.org/x/crypto都提供了加密算法和其他密码学功能，但crypto更注重于提供标准化的和已知安全的算法，而golang.org/x/crypto则提供了一些扩展的算法和功能，并且在某些情况下可能会比标准库更有用。

"golang.org/x/crypto/curve25519"
"golang.org/x/crypto/ed25519"
  • golang.org/x/crypto/curve25519实现了基于X25519曲线的Diffie-Hellman密钥交换算法。
  • golang.org/x/crypto/ed25519实现了基于Ed25519曲线的EdDSA数字签名算法。
  1. 都基于新兴的Edwards曲线族,性能和其他特性更优于传统的椭圆曲线。
  2. 都由D. J. Bernstein教授设计,有相当的学术和工程实践支撑。
  3. Curve25519和Ed25519都属于比较先进和安全的算法选择。

主要区别在于:
使用的椭圆曲线参数不同。curve25519使用Edwards曲线,ed25519使用twisted Edwards曲线。实现的具体算法不同。curve25519实现密钥交换,ed25519实现数字签名。

演示demo（X25519-DH协议的基本流程,以及如何使用curve25519包实现该协议）

X25519-DH协议的基本流程,以及如何使用curve25519包实现该协议：

  1. Alice和Bob分别生成X25519私钥privA和privB。
  2. 基于私钥和标准基点curve25519.Basepoint计算公钥pubA和pubB。
  3. 公钥交换通道在这里简化为直接使用两个公钥。
  4. Alice使用Bob的公钥pubB和自己的私钥privA计算共享密钥secretA。Bob同样可以计算secretB。
  5. 验证两个共享密钥是否匹配,如果匹配则密钥交换成功。
package main

import (
	"bytes"
	"crypto/rand"
	"fmt"
	"golang.org/x/crypto/curve25519"
	"io"
)

func main() {
	// Alice生成私钥
	alicePrivKey := make([]byte, 32)
	rand.Read(alicePrivKey)

	// Alice生成公钥并发送给Bob
	alicePubKey, err := curve25519.X25519(alicePrivKey, curve25519.Basepoint)
	if err != nil {
		fmt.Println(err)
		return
	}
	//sendToBob(alicePubKey)

	// Bob生成私钥
	bobPrivKey := make([]byte, 32)
	rand.Read(bobPrivKey)

	// Bob接收Alice的公钥
	//alicePubKey := receiveFromAlice()

	// Bob生成公钥并发送给Alice
	bobPubKey, err := curve25519.X25519(bobPrivKey, curve25519.Basepoint)
	if err != nil {
		fmt.Println(err)
		return
	}
	//sendToAlice(bobPubKey)

	// Alice接收Bob的公钥
	//bobPubKey := receiveFromBob()

	// Alice使用自己的私钥和Bob的公钥生成共享密钥
	aliceSharedKey, err := curve25519.X25519(alicePrivKey, bobPubKey)
	if err != nil {
		fmt.Println(err)
		return
	}

	// Bob使用自己的私钥和Alice的公钥生成共享密钥
	bobSharedKey, err := curve25519.X25519(bobPrivKey, alicePubKey)
	if err != nil {
		fmt.Println(err)
		return
	}

	//打印共享密钥
	fmt.Println(aliceSharedKey)
	fmt.Println(bobSharedKey)
	// 比较Alice和Bob生成的共享密钥是否相等
	if bytes.Equal(aliceSharedKey, bobSharedKey) {
		fmt.Println("Shared keys match!")
	} else {
		fmt.Println("Shared keys do not match!")
	}

	// Alice和Bob使用相同的共享密钥进行加密通信
	fmt.Println("Alice and Bob established a shared key!")
}

curve25519.Basepoint是一个预定义的常量,代表X25519标准curve上的基点。

标量乘法(scalar multiplication)或者标量点乘(scalar point multiplication)指的是:取一个标量k和一个点P,计算kP,获得另一个点Q。

举个例子,在椭圆曲线密码学中,每个用户选择一个标量作为私钥。基点是曲线上的一个标准定点。用户首先计算自己的公钥:

公钥 = 私钥 * 基点

然后,两个用户交换各自的公钥,并分别计算共享密钥:

共享密钥A = 本地私钥 * 对方公钥
共享密钥B = 对方私钥 * 本地公钥

最后验证两个共享密钥是否相同,如果相同则密钥交换成功。

在noise协议中，cipher_suite.go

func (dh25519) DH(privkey, pubkey []byte) ([]byte, error) {
	return curve25519.X25519(privkey, pubkey)
}

四、参考

[推荐]五次方程（三）群论入门 隐藏在根与系数关系中的秘密
参考URL: https://www.bilibili.com/video/BV1Wb41187wA/
Diffie-Hellman密钥交换算法简单原理（颜色演示）
参考URL: https://www.bilibili.com/video/BV1hP411w7QK
[双语字幕] 史上最好的群论入门
参考URL: https://www.bilibili.com/video/BV1PM411g7o8/
[推荐]有理数“有道理”，无理数“没道理”吗？
参考URL: https://www.toutiao.com/article/6977168656883024414/
面试官你不要说我不懂TLS了
参考URL: https://www.toutiao.com/article/7031701667993141796/
Asecuritysite.com
[推荐]代数结构入门：群、环、域、向量空间
参考URL: https://www.toutiao.com/article/6824995787190043151/
Curve25519椭圆曲线算法GPU高速实现
参考URL: https://www.doc88.com/p-9951742356056.html

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/580651.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Django实现人脸识别登录

Django实现人脸识别登录

Django实现人脸识别登录 Demo示例下载 1、账号密码登录 2、人脸识别登录 3、注册 4、更改密码 5、示例网站 点我跳转 一、流程说明 1、注册页面：前端打开摄像头，拍照，点击确定后上传图像 2、后端获取到图像，先通过face_recognition第三方库识别是否能够获取到人脸特征…
阅读更多...
开闭原则正确姿势, 使用AOP优雅的记录日志, 非常的哇塞

开闭原则正确姿势, 使用AOP优雅的记录日志, 非常的哇塞

&#x1f473;我亲爱的各位大佬们好&#x1f618;&#x1f618;&#x1f618; ♨️本篇文章记录的为 JDK8 新特性 Stream API 进阶 相关内容&#xff0c;适合在学Java的小白,帮助新手快速上手,也适合复习中&#xff0c;面试中的大佬&#x1f649;&#x1f649;&#x1f649;。 …
阅读更多...
使用腾讯云服务器快速搭建网站教程

使用腾讯云服务器快速搭建网站教程

已经有了腾讯云服务器如何搭建网站&#xff1f;腾讯云服务器网以腾讯云服务器&#xff0c;借助宝塔面板搭建Web环境&#xff0c;然后使用WordPress博客程序搭建网站&#xff0c;大致分为三步&#xff0c;首先购买腾讯云服务器&#xff0c;然后在腾讯云服务器上部署宝塔面板&…
阅读更多...
Vue + Vite 构建 自己的ChartGPT 项目

Vue + Vite 构建 自己的ChartGPT 项目

前期回顾 两分钟学会 制作自己的浏览器 —— 并将 ChatGPT 接入_彩色之外的博客-CSDN博客自定义浏览器&#xff0c;并集合ChatGPT&#xff0c;源码已公开https://blog.csdn.net/m0_57904695/article/details/130467253?spm1001.2014.3001.5501 目录 效果图 代码步骤&am…
阅读更多...
【Linux】软件包管理器/编辑器/yum是应用商店？/vim编辑器什么？

【Linux】软件包管理器/编辑器/yum是应用商店？/vim编辑器什么？

本文思维导图&#xff1a; 文章目录 Linux软件安装关于Linux的软件生态 1.Linux软件包管理器&#xff1a;yum到底是什么关于yum指令&#xff1a;关于yum源 2. rzsz指令1. Linux编辑器——vim编辑器vim编辑器的三种主要模式vim编辑器命令模式常用快捷键&#xff1a;vim操作总结…
阅读更多...
spring(事务管理)

spring(事务管理)

事物可以看做是由对数据库若干操作组成的一个单元 事务的作用就是为了保证用户的每一个操作都是可靠的&#xff0c;事务中的每一步操作都 必须成功执行&#xff0c;只要有发生异常就回退到事务开始未进行操作的状态,这些操作 要么都完成&#xff0c;要么都取消&#xff0c;从而…
阅读更多...
Linux：/dev/tty、/dev/tty0 和 /dev/console 之间的区别

Linux：/dev/tty、/dev/tty0 和 /dev/console 之间的区别

在Linux操作系统中&#xff0c;/dev/tty、/dev/tty0和/dev/console是三个特殊的设备文件&#xff0c;它们在终端控制和输入/输出过程中扮演着重要的角色。尽管它们看起来很相似&#xff0c;但实际上它们之间存在一些重要的区别。本文将详细介绍这三个设备文件之间的区别以及它们…
阅读更多...
浅谈如何fltk项目编译和实现显示中文

浅谈如何fltk项目编译和实现显示中文

目录 一、编译 二、中文显示如何处理&#xff1a; 2.1在发文2天前突然发现&#xff0c;我这个界面显示英文出现问题了&#xff0c;开始我的搜索之旅&#xff0c;一些参考页面有碰到问题也可以看看&#xff1a; 2.2、 那就开始翻翻官方自带的例程吧&#xff0c;看看他如何显…
阅读更多...
Join的连接原理

Join的连接原理

1. 连接简介 1.1 连接的本质 连接就是把各个表中的记录都取出来进行一次匹配&#xff0c;并把匹配后的组合发送给客户端。如果连接查询中的结果集中包含一个表中的每一条记录与另一个表中的每一条记录相互匹配的组合&#xff0c;那么这样的结果集就可以称为笛卡尔积。 1.2 连…
阅读更多...
计算机网络基础知识（七）—— 什么是HTTPS协议？你听我“瞎掰”

计算机网络基础知识（七）—— 什么是HTTPS协议？你听我“瞎掰”

文章目录 01 | 工作原理02 | SSL/TLS协议2.1 | 握手协议2.2 | 更换密码协议&#xff08;Change Cipher Spec Protocol&#xff09;2.3 | 警告协议&#xff08;Alert Protocol&#xff09;2.4 | 应用数据协议&#xff08;Application Data Protocol&#xff09; 03 | 加密算法3.…
阅读更多...
CSRF及SSRF漏洞案例讲解（29）

CSRF及SSRF漏洞案例讲解（29）

讲解一下这个图片&#xff0c;用户在浏览器登陆银行界面发送一个请求&#xff0c;通过转账&#xff0c;转载的数据包假如是下面那串字符&#xff0c;黑客呢就自己一个网站或控制一个网站&#xff0c;去写入一个代码&#xff0c;这个代码就是请求这个数据包&#xff0c;刚好这个…
阅读更多...
人工智能学习07--pytorch19--目标检测：常见指标（mAP计算+coco评价标准）

人工智能学习07--pytorch19--目标检测：常见指标（mAP计算+coco评价标准）

怎样才算正确检测到一个目标&#xff1f; 什么是IOU&#xff1a; https://blog.csdn.net/qq_51831335/article/details/125719420 mAP计算方法&#xff1a; 假设针对某一类别的AP情况 TP&#xff1a;预测正确的边界框个数。预测边界框与GT-box的IOU>0.5 FP&#xff1a;假…
阅读更多...
原工程运行正常，重新复制一份后再 npm install 后再运行就报错的解决办法

原工程运行正常，重新复制一份后再 npm install 后再运行就报错的解决办法

原工程&#xff0c;运行正常 将刚刚的工程复制一份呢&#xff0c;重新 npm install 再 npm run serve 就报错 出现这个问题十之八九都是依赖的问题。有可能是因为这个工程里面之前安装过一些东西&#xff0c;后来莫名其妙的就把 package.json 里面相关的依赖给删掉了。但由于原…
阅读更多...
lwIP 开发指南

lwIP 开发指南

目录 lwIP 初探TCP/IP 协议栈是什么TCP/IP 协议栈架构TCP/IP 协议栈的封包和拆包 lwIP 简介lwIP 源码下载lwIP 文件说明 MAC 内核简介PHY 芯片介绍YT8512C 简介LAN8720A 简介 以太网接入MCU 方案 lwIP 无操作系统移植lwIP 带操作系统移植ARP 协议ARP 协议的简介ARP 协议的工作流…
阅读更多...
uni-app项目运行和项目结构目录讲解

uni-app项目运行和项目结构目录讲解

UNI-APP学习系列 uni-app项目运行和项目结构目录讲解 文章目录 UNI-APP学习系列前言总结 前言 UNI-APP学习系列之uni-app项目运行和项目结构目录讲解 运行项目 使用 pnpm 包管理工具 # 查看是否安装pnpmpnpm -v# 无则安装npm install -g pnpm下载依赖 pnpm i运行pnpm dev:h…
阅读更多...
Window的创建

Window的创建

Window的创建 上一篇说到了Window和WindowManager的关系并且讲述了WindowManager如何添加Window与Window内部的三个方法的实现 这篇主要讲几个常见的Window的创建比如Activity,Dialog和Toast 其中Activity属于应用Window Dialog属于子Window Toast属于系统Window z-order…
阅读更多...
python基础知识(二):变量和常用数据类型

python基础知识(二):变量和常用数据类型

目录 1. 变量1.1 变量的定义1.2 变量的命名规则 2. 常用数据类型2.1 字符串2.1.1 字符串的常用方法2.1.1.1 title()方法&#xff1a;将字符串中的单词首字母大写2.1.1.2 upper()方法&#xff1a;将字符串中的单词字母全大写2.1.1.3 lower()方法&#xff1a;将字符串中的单词字母…
阅读更多...
什么是分段路由？如何在网络中实施分段路由？

什么是分段路由？如何在网络中实施分段路由？

在计算机网络中&#xff0c;分段路由&#xff08;Subnetting&#xff09;是一种将一个大的网络划分为多个较小子网的技术。它允许网络管理员更有效地分配 IP 地址和管理网络流量。本文将详细介绍分段路由的概念、原理以及如何在网络中实施分段路由。 1. 分段路由的概念 分段路…
阅读更多...
【深入浅出Spring Security（一）】Spring Security的整体架构

【深入浅出Spring Security（一）】Spring Security的整体架构

Spring Security的整体架构 一、整体架构认证&#xff08;Authentication&#xff09;AuthenticationManagerAuthentication登录后的数据保存&#xff08;SecurityContextHolder&#xff09; 授权&#xff08;Authorization&#xff09;ConfigAttribute 二、总结 这篇博客所述主…
阅读更多...
CISCN 2023 初赛 pwn——Shellwego 题解

CISCN 2023 初赛 pwn——Shellwego 题解

这是一个用go语言写的elf程序&#xff0c;没有PIE。这也是本蒟蒻第一次解go pwn题&#xff0c;故在此记录以便参考。 而且&#xff0c;这还是一个全部符号表被抠的go elf&#xff0c;直接面对一堆不知名的函数实在有些应付不来&#xff0c;因此在比赛时委托逆向的队友把符号表…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023