目录
一、图的定义和基本术语
二、图的类型定义
三、图的存储结构
1、数组(邻接矩阵)表示法
二、邻接表(链式)表示法
三、图的邻接表的存储表示
四、十字链表与邻接多重链表
(1)十字链表
(2)邻接多重表
五、图的遍历
(1)深度优先遍历(DFS):
(2)广度优先遍历 (BFS)
六、图的应用
1、生成树 与 最小生成树
构造最小生成树 (MST性质)
构造最小生成树方法一: prim算法
构造最小生成树方法二:Kruskal
2、最短路径
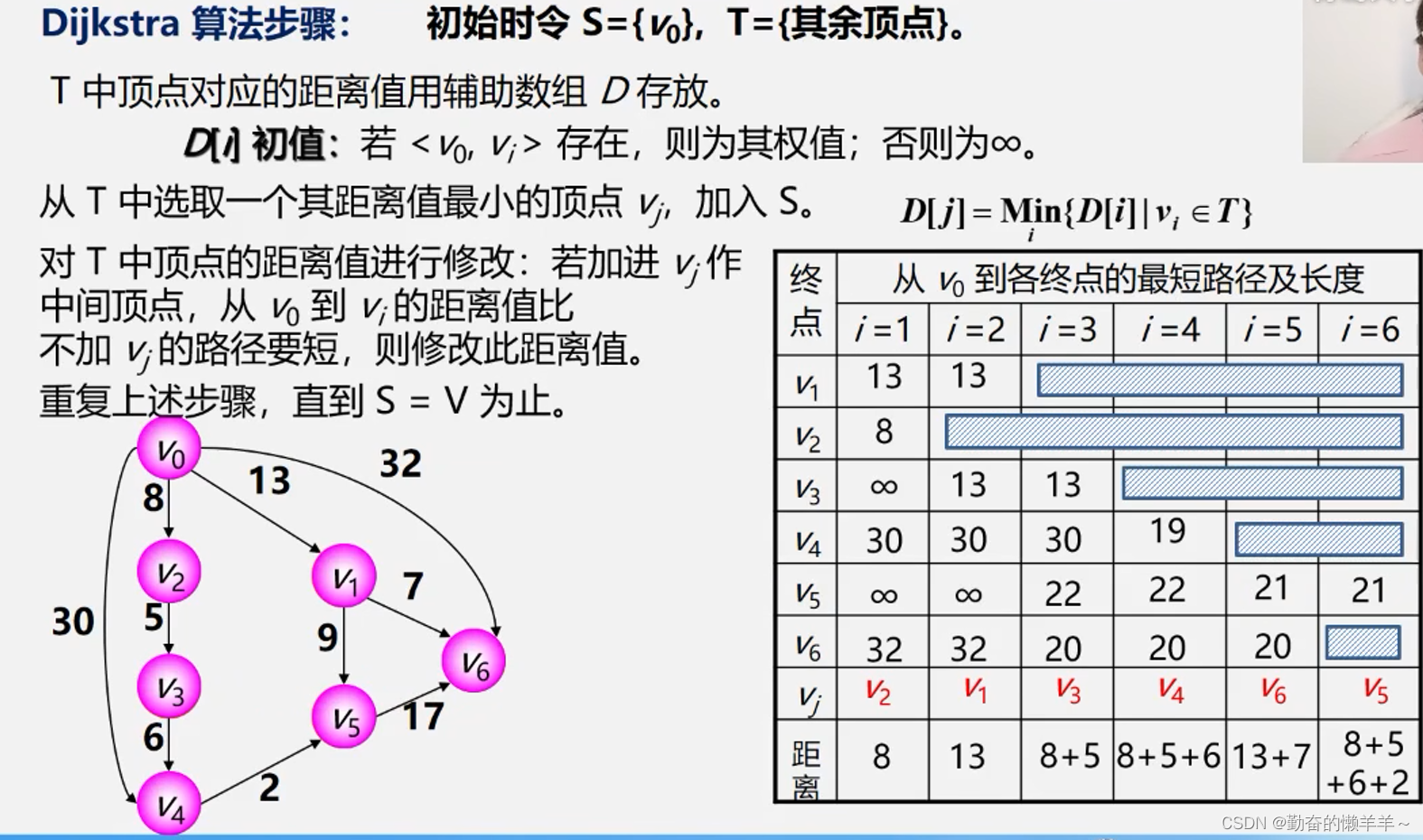
(1)单源最短路径------Dijkstra(迪杰斯特拉)算法O(n^3)
编辑
(2)所有顶点间的最短路径------Floyd(费洛伊德)算法O(n^3)
3、拓扑排序 和 关键路径
(1)AOV网和拓扑排序
(2)AOE网和关键路径
一、图的定义和基本术语
图:G=(V,E) Graph = (Vertex,Edge)
V:顶点(数据元素)的有穷非空集合
E:边的有穷集合
无向图:每条边都是无方向的。
有向图:每条边都是有方向的。
完全图:任意两个点都有一条边相连
稀疏图:有很少边或弧的图(e<nlogn)
稠密图:有较多边或弧的图
网:边/弧带权的图
邻接:有边/弧相连的两个顶点之间的关系。
存在(vi,vj)则称vi和vj互为邻接点;
存在<vi,vj>则称vi邻接到vj,vj邻接于vi
关联(依附):边/弧与顶点之间的关系
存在(vi,vj)/<vi,vj>,则称该边/弧关联于vi和vj
顶点的度:与该顶点相关联的边的数目,记TD(v)
在有向图中,顶点的读等于该顶点的出度与入度之和。
路径:接续的边构成的顶点序列。
路径长度:路径上边或弧的数目/权值之和。
回路(环):第一个顶点和最后一个顶点相同的路径。
简单路径:除路径起点和终点可以相同外,其余顶点均不相同的路径。
简单回路(简单环):除路径起点和终点相同外,其余顶点均不相同的路径。
连通图(强连通图):在无(有)向图G= (V,{E})中,若对任何两个顶点v、u都存在从v到u的路径,则称G是连通图(强连通图)。
权与网:图中边或弧所具有的相关数称为权,表明从一个顶点到另一个顶点的距离或耗费。
子图:a图边/弧、顶点都是b图的边/弧、顶点的子集,a图就是b图的子图。
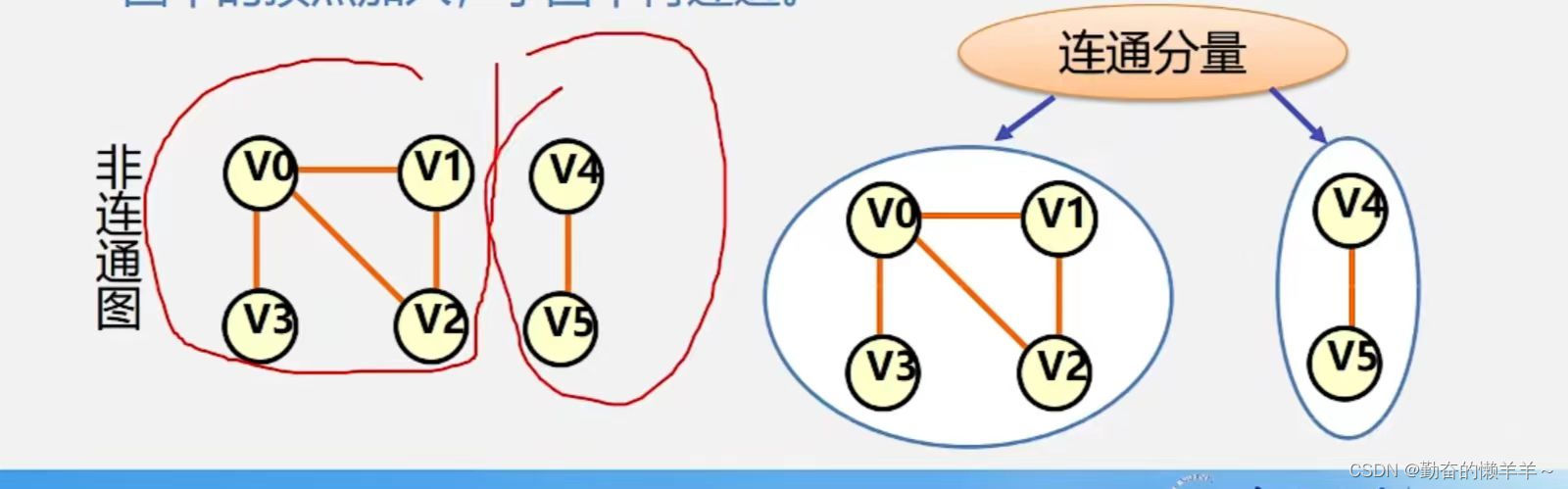
连通分量(强连通分量):
无向图G的极大连通子图称为G的连通分量。
有向图G的极大强连通子图称为G的强连通分量。
极小连通子图:该子图是G的连通子图,在该子图中删除任何一条边/弧,子图不再连通。
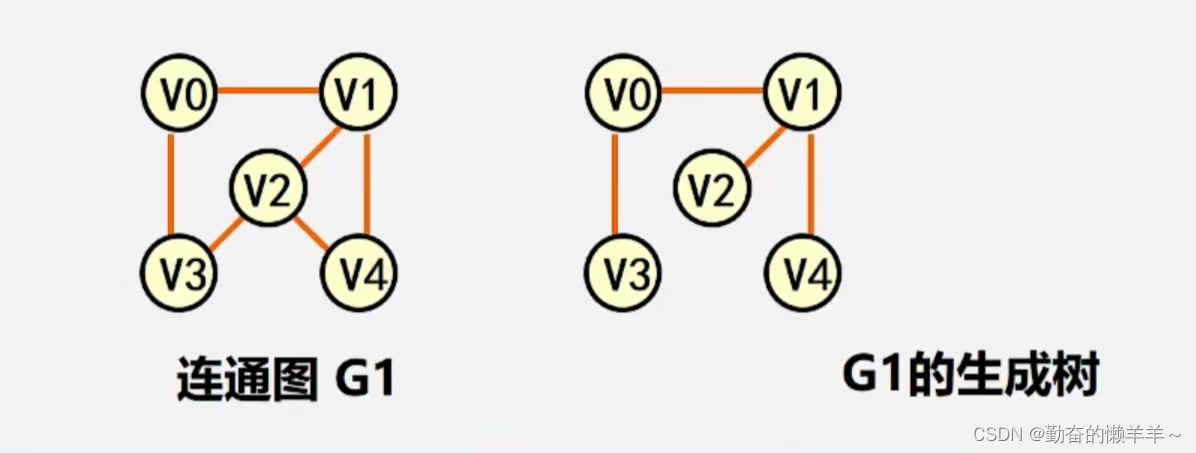
生成树:包含无向图G所有顶点的极小连通子图。
生成森林:对非连通图,由各个连通分量的生成树的集合。
二、图的类型定义
图的抽象数据类型定义如下:
ADT Graph{
数据对象V:具有相同特性的数据元素的集合,称为顶点集。
数据关系R:R={VR}
VR={<V,W>|<v,W>|v,WEV^p(v,w),
<v,w>表示从v到w的弧,P(v,w)定义了弧<v,w>的信息}
基本操作P:
Create_Graph():图的创建操作。
初始条件:无。
操作结果:生成一个没有顶点的空图G。
GetVex(G,v):求图中的顶点v的值。
初始条件:图G存在,v是图中的一个顶点。
操作结果:生成一个没有顶点的空图G。CreateGraph(&G,V,VR)
初始条件:V是图的顶点集,VR是图中弧的集合。
操作结果:按V和VR的定义构造图G。
DFSTraverse(G)
初始条件:图G存在。
操作结果:对图进行深度优先遍历。
BFSTraverse(G)
初始条件:图G存在。
操作结果:对图进行广度优先遍历。
}ADT Graph
三、图的存储结构
图的逻辑结构:多对多
图没有顺序存储结构,但可以借助二维数组来表示元素间的关系
重点介绍:
邻接矩阵(数组)表示法
邻接表(链式)表示法
1、数组(邻接矩阵)表示法
建立一个顶点表(记录各个顶点信息)和一个邻接矩阵(表示各个顶点之间关系)。

邻接矩阵:
(一)无向图的邻接矩阵表示法:
(1)无向图的邻接矩阵是对称的。
(2)顶点i的度 = 第i行(列)中1的个数;
(3)完全图的邻接矩阵中,对角线元素为0,其余为1。
(4)初始化邻接矩阵时,w均为0,构造邻接矩阵时,w为1
(二)有向图的邻接矩阵表示法
注:行表示出度边,列表示入度边。
分析:
(1)有向图的邻接矩阵可能是不对称的。
(2)顶点的出度=第i行元素之和
顶点的入度=第i列元素之和
顶点的度=第i行元素之和+第i列元素之和
(三)网(及有权图)的邻接矩阵表示法
1、有向网
2、无向网
(1)输入总项点数和总边数。
(2)依次输入点的信息存入顶点表中。
(3)初始化邻接矩阵,使每个取值初始化为极大值。
(4)构造邻接矩阵。
邻接矩阵-有什么好处?
(1)直观、简单、好理解
(2)方便检查任意一对顶点间是否存在边
(3)方便找任一顶点的所有“邻接点”(有边直接相连的顶点)
(4)方便计算任一顶点的“度”(从该点发出的边数为“出度”,指向该点的边数为“入度”)
(5)无向图:对应行(或列)非0元素的个数
(6)有向图:对应行非0元素的个数是“出度”;对应列非0元素的个数是“入度”邻接矩阵-有什么坏处?
(1)不便于增加和删除顶点。
(2)浪费空间-存稀疏图(点很多而边很少)有大量无效元素。O(n^2)
(3)对稠密图(特别是完全图)还是很合算的。
(4)浪费时间-统计稀疏图中一共有多少条边。
二、邻接表(链式)表示法

顶点:按编号顺序将顶点数据存储在一维数组中;
关联同一顶点的边(以顶点为尾的弧):用线性链表存储。
(1)无向图:
特点:
(1)邻接表不唯一
(2)若无向图中有n个顶点,e条边,则其邻接表需n个头结点和2e个表结点。适合存储稀疏图。 空间:O(n+2e)
(3)无向图中vi的度为第i个单链表中结点数。
(2)有向图

邻接表特点:
顶点vi的出度为第i个单链表中的结点个数。
顶点vi的入度为整个单链表中邻接点域值是i-1的结点个数。
找出度容易,找入度难。
相反的,逆邻接表找入度容易,找出度难。
三、图的邻接表的存储表示
(1)顶点的结点结构
typedef struct VNode { VerTexType data;//顶点信息 ArcNode* firstarc;//指向第一条依附该顶点的边的指针 }VNode,AdjList[MVNum];//AdjList表示邻接表类型(2)弧(边)的结点结构
typedef struct ArcNode { int adjvex; struct ArcNode* nextarc;//指向下一条边 OtherInfo info;//和边相关的信息 }ArcNode;(3)图的结构定义
typedef struct { AdjList vertices;//vertex的复数 int vexnum, arcnum;//图的当前顶点数和弧数 }ALGraph;
采用邻接表法创建无向网
(1)输入总顶点数和总边数
(2)建立顶点表
依次输入点的信息存入顶点表中
使每个表头结点的指针域初始化为NULL
(3)创建邻接表
依次输入每条边依附的结点
确定两个顶点的序号i和j,建立边结点
将此边结点分别插入到vi和vj对应的两个边链表的头部。
Status CreateUDG(ALGraph& G) { cin >> G.vexnum >> G.arcnum;//输入总顶点数,总边数 for (i = 0; i < G.vexnum; ++i) { cin >> G.vertices[i].data;//输入顶点值 G.vertices[i].firstarc = NULL;//初始化表头结点的指针域 } for (k = 0; k < G.vexnum; ++k)//输入各边,构造邻接表 { cin >> v1 >> v2;//输入一条边依附的两个顶点 j = LocateVex(G, v1);//找到两个顶点的下标 i = LocateVex(G, v2); } p1 = new ArcNode;//生成一个新的边结点 p1->adjvex = j;//邻接点序号为j p1->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc = p1;//将新节点*p1插入顶点vi的边表头部 p2 = new ArcNode;//生成另一个对称的新的边结点*p2 p2->adjvex = i;//邻接点序号为i p2->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc = p2;//将新节点*p2插入顶点vj的边表头部 return ok; }
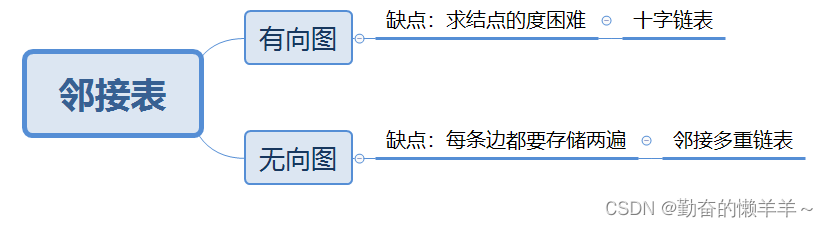
四、十字链表与邻接多重链表
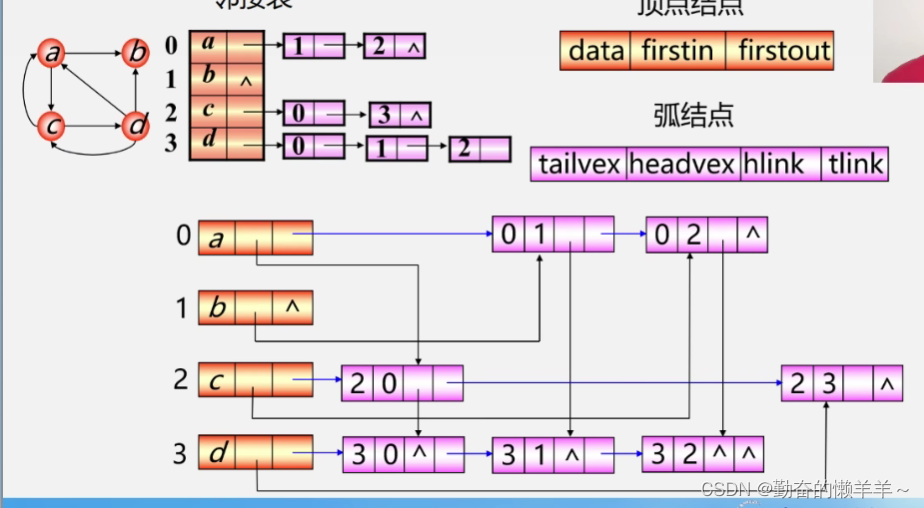
(1)十字链表
十字链表(Orthogonal List)是有向图的另一种链式存储结构。我们也可以把它看成是将有向图的邻接表和逆邻接表结合起来形成的一种链表。
有向图中的每一条弧对应十字链表中的一个弧结点,同时有向图中的每个顶点在十字链表中对应有一个结点,叫做顶点结点。
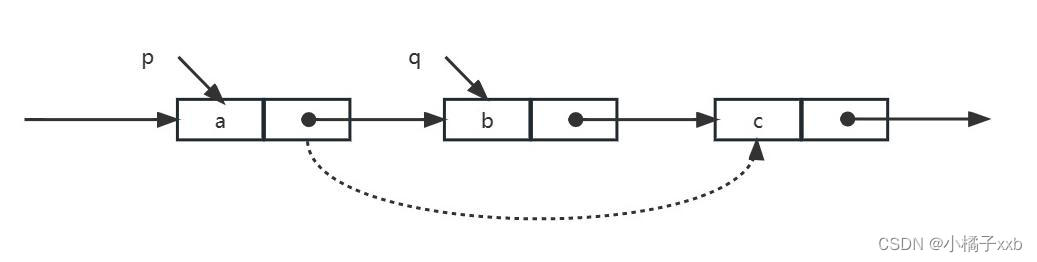
(2)邻接多重表
边结点:
| mark | ivex | ilink | jvex | jlink | info |
mark:标记域,标记此边是否被搜索过。
ivex:该边依附的两个顶点在表头数组中位置
ilink:指向依附于ivex的下一条边
jvex:指向依附于jvex的下一条边
info:其他信息

五、图的遍历
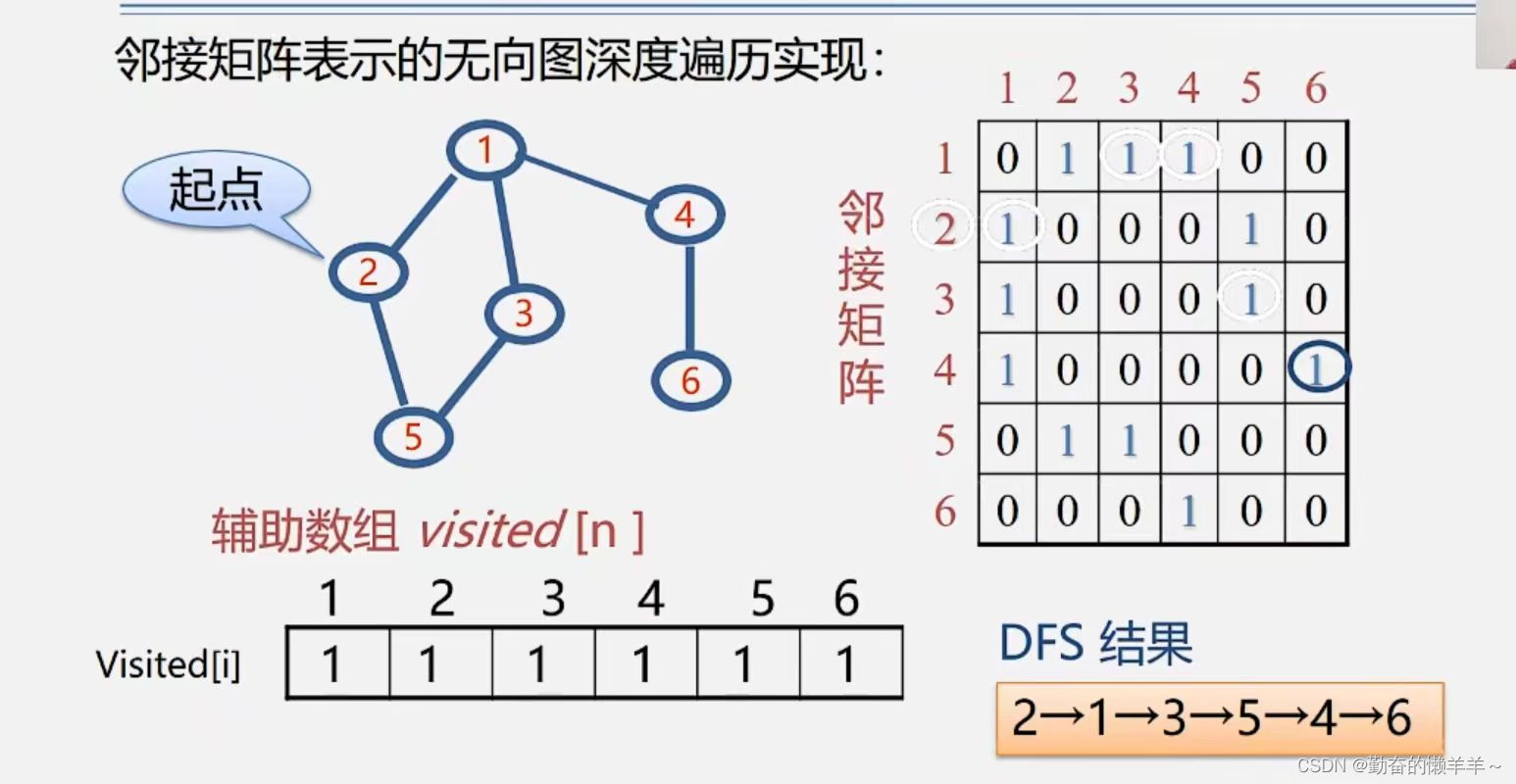
(1)深度优先遍历(DFS):
方法:
■在访问图中某一起始顶点v后,由v出发,访问它的任一邻接顶点W1
■再从w1出发,访问与W邻接但还未被访问过的顶点W2
然后再从W2出发,进行类似的访问,...
如此进行下去,直至到达所有的邻接顶点都被访问过的顶点u为止。
接着,退回一步,退到前一次刚访问过的顶点,看是否还有其它没有被访问的邻接顶点。
如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问;
如果没有,就再退回一步进行搜索。重复上述过程,直到连通图中所有顶点都被访问过为止。
DFS算法效率分析:
用邻接矩阵来表示图,遍历图中每个顶点都要从头扫描该顶点所在行,时间复杂度为O(n^2)
用邻接表来表示图,虽然有2e个表结点,但只需要扫描e个结点即可完成遍历,加上访问n个头结点的时间,时间复杂度为O(n+e)。
稠密图适合在邻接矩阵上进行深度遍历。
稀疏图适合在邻接表上进行深度遍历。
(2)广度优先遍历 (BFS)
方法:从图的某一结点出发,首先依次访问该结点的所有邻点Vii, Vi2,..., Vin再按这些顶点被访问的先后次序依次访问与它们相邻接的所有未被访问的顶点
重复此过程,直至所有顶点均被访问为止。广度优先遍历结果:v1->v2->v3->v4->v5->v6->v7->v8
BFS算法效率分析:
时间复杂度:
邻接矩阵:O(n^2)
邻接表:O(n+e)
空间复杂度:
都是O(n)(借用了堆栈或队列)
六、图的应用
1、生成树 与 最小生成树
构造最小生成树 (MST性质)
最小生成树:权值和最小的生成树,也叫最小代价生成树。
构造最小生成树方法一: prim算法
构造最小生成树方法二:Kruskal
2、最短路径
(1)单源最短路径------Dijkstra(迪杰斯特拉)算法O(n^3)
(2)所有顶点间的最短路径------Floyd(费洛伊德)算法O(n^3)

3、拓扑排序 和 关键路径

AOV网解决拓扑排序问题
AOE网解决关键路径问题
(1)AOV网和拓扑排序
拓扑排序:将AOV网写成线性序列
拓扑序列并不唯一。
如何检测AOV网中是否存在环?
如果网中所有顶点都在拓扑序列中,则不存在环。
(2)AOE网和关键路径
关键路径