题目链接
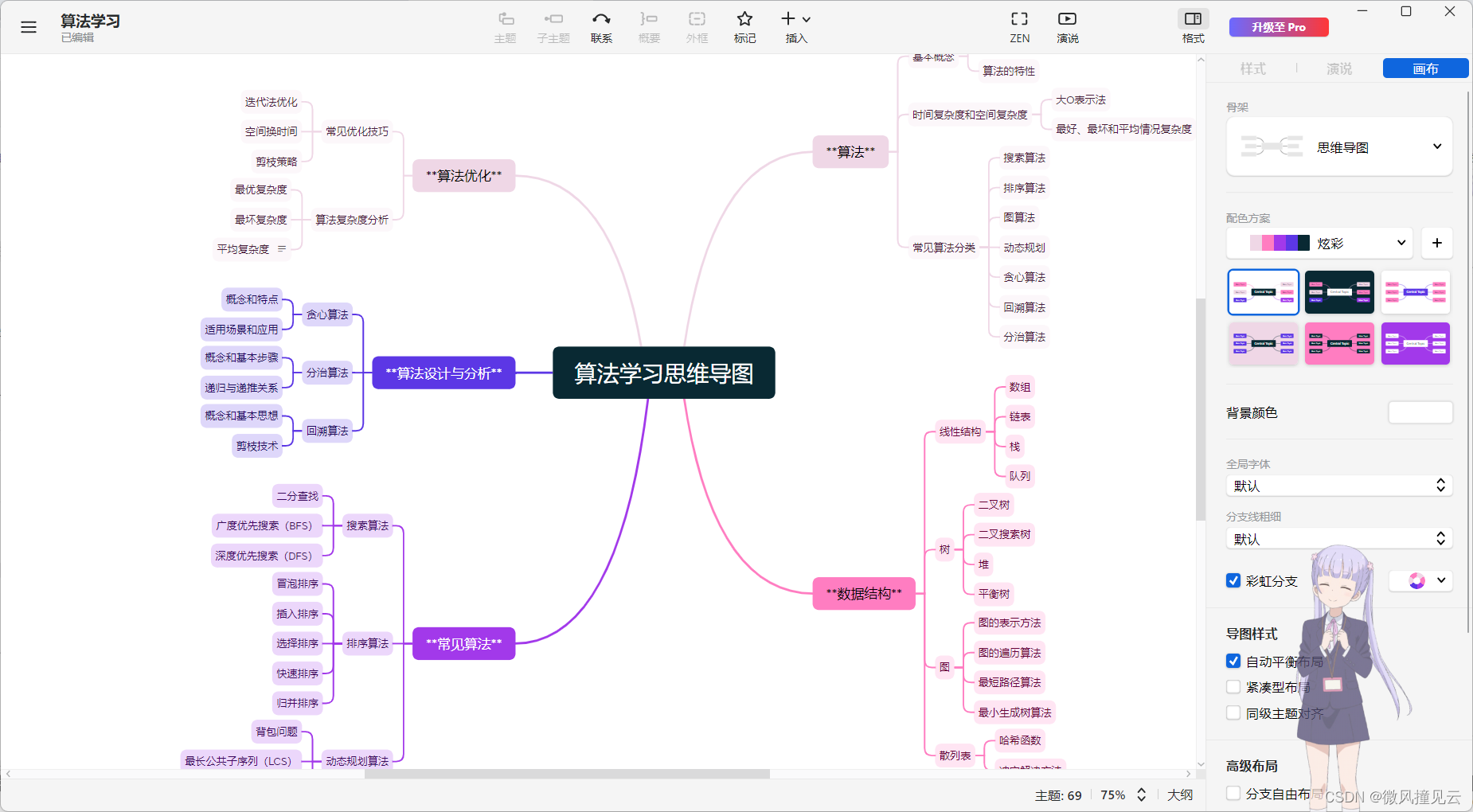
柱状图中最大的矩形
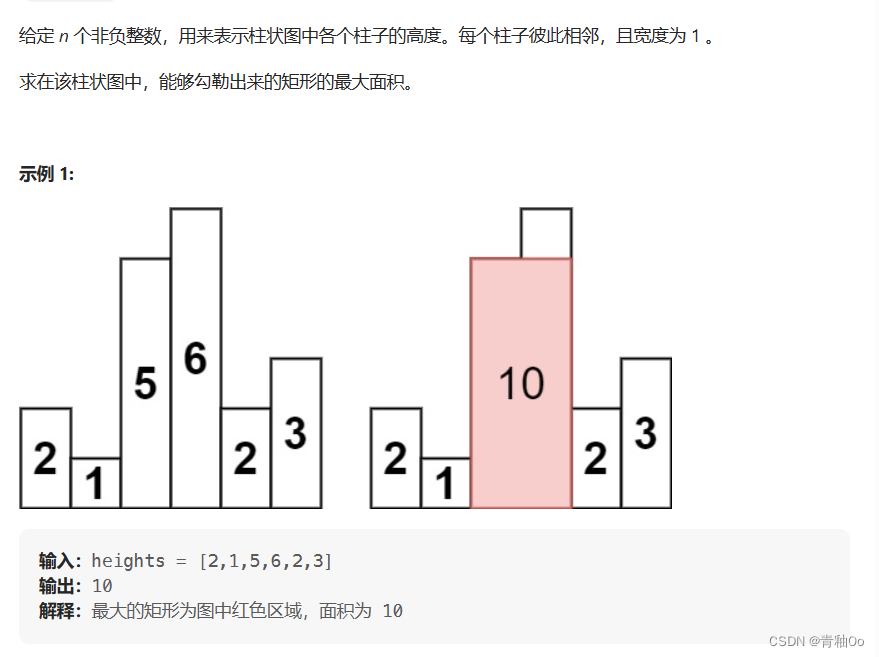
题目描述
注意点
- 无
解答思路
- 暴力破解根据每根柱子x以x的高度作为矩形的高度找到其相邻能组成矩形的柱子,遍历所有柱子即可找到最大矩形,但是时间复杂度是O(n²),最终运行结果也超时了
- 上面暴力破解的方法中大多数柱子都可能被遍历多次,这极大地降低了效率,所以考虑有没有一种方法遍历一次柱子即可,参照题解要想解决此题,只需要明确一点,遍历每个高度,是要以当前高度为基准,寻找最大的宽度,组成最大的矩形面积那就是要找左边第一个小于当前高度的下标left,再找右边第一个小于当前高度的下标right,那宽度就是这两个下标之间的距离了,用单调栈就可以很方便确定这两个边界了,单调栈其存储的是高度单调递增的柱子(也有相等的情况,放在后续考虑),且存储的是柱子的坐标(方便确定边界)。
- 在遍历到某个柱子k相比于栈顶柱子j的高度低时,此时就已经找到了栈顶柱子j左右两侧第一个小于j的高度的柱子坐标,也就可以确定栈顶柱子j作为高度的矩形最大面积,边界也就是柱子i和k的坐标之间的距离,确定了柱子j作为高度的矩形最大面积后就可以将其在栈中排除掉,以此类推,便确定了多数柱子为高度的最大面积(注意只是确定了该柱子的高度作为矩形高度的最大矩形,其仍有可能只用高度的一部分与其他柱子共同组成面积更大的矩形,但是其是由后面的柱子所决定的),且保证了单调栈中的柱子高度是递增的
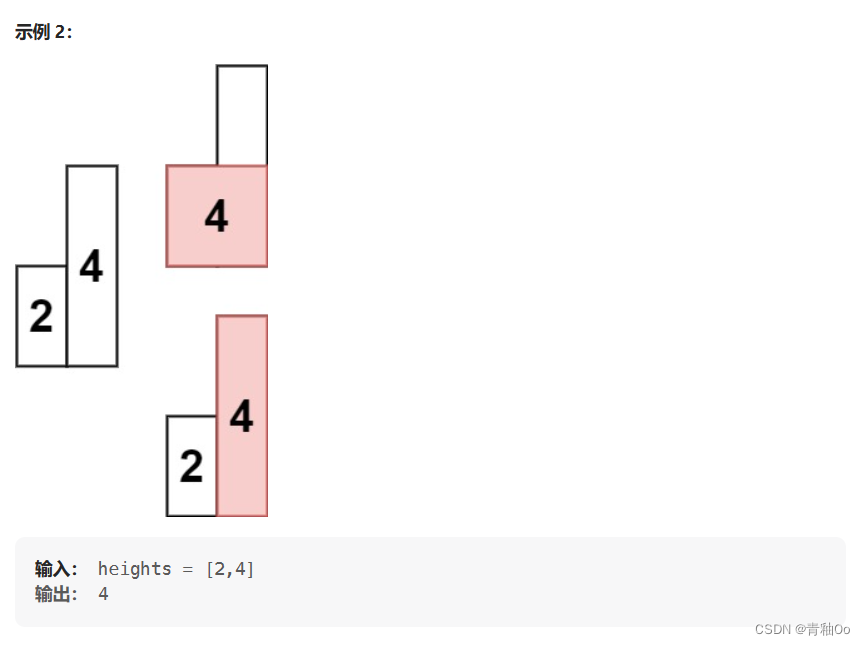
- 在一次遍历后确定了多数柱子组成的最大矩形后,栈中还有可能剩有柱子(此时栈是单调递增的),需要对剩下柱子所能组成矩形的最大面积进行计算,此时高度就是栈顶柱子高度,右边界就是第一次弹出的栈顶柱子坐标(后续其余柱子的高度和右边界会有变化,但是右边界始终都是该坐标,因为后续柱子都肯定能与之前的柱子组成矩形),而左边界要分情况考虑:一是弹出栈顶柱子后此时栈中无柱子,则说明该柱子左侧所有的柱子都能与其组成矩形,左边界为0;二是弹出栈顶柱子后此时新的栈顶柱子与其高度相等,则其能与新的栈顶柱子组成矩形,以此类推,需要找到第一个与栈顶柱子高度不相同的柱子的坐标作为左边界;三是弹出栈顶柱子后此时新的栈顶柱子与其高度不相等,则新的栈顶柱子高度肯定低于其高度,无法组成矩形,左边界就是新的栈顶柱子坐标
代码
class Solution {
public int largestRectangleArea(int[] heights) {
int n = heights.length, res = 0;
// 栈用于存储递增的柱子的坐标(只会单调递增,也有相等的情况,如果高度递减则会进行出栈相关操作)
Deque<Integer> stk = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
// 找到了递减的柱子k,则可以算出其前一个更高的柱子j作为高度的最大面积
while (stk.size() != 0 && heights[stk.peek()] > heights[i]) {
int idx = stk.pop();
// 左边界为柱子j的前一个更低的柱子k,又因为栈只会单调递增,所以就是栈中相邻的柱子(注意考虑边界情况)
int left = stk.size() != 0 ? stk.peek() : -1;
int area = heights[idx] * (i - left - 1);
res = Math.max(res, area);
}
stk.push(i);
}
if (stk.size() == 0) {
return res;
}
// 栈不为空时对剩余单调递增且不确定最大面积的柱子进行计算
int right = stk.peek();
while (stk.size() != 0) {
int idx = stk.pop();
// 此时对栈中相邻且高度相等的柱子也要进行考虑,其能共同组成一个矩形
while (stk.size() != 0 && heights[idx] == heights[stk.peek()]) {
stk.pop();
}
int left = stk.size() != 0 ? stk.peek() : -1;
int area = heights[idx] * (right - left);
res = Math.max(res, area);
}
return res;
}
}
关键点
- 要想解决此题,只需要明确一点,遍历每个高度,是要以当前高度为基准,寻找最大的宽度,组成最大的矩形面积那就是要找左边第一个小于当前高度的下标left,再找右边第一个小于当前高度的下标right,那宽度就是这两个下标之间的距离了,用单调栈就可以很方便确定这两个边界了
- 在第一次遍历只能计算出左右两侧都有比其高度更低的柱子的最大矩形面积,栈中剩余的柱子都说明右侧没有比其高度更低的柱子,所以还需要对栈中剩余的柱子组成的最大矩形面积进行计算,其右边界都是一样的(最初栈顶柱子的坐标),左边界则需要考虑边界及与其柱子高度相等的情况