文心一言 VS 讯飞星火 VS chatgpt （24）-- 算法导论4.2 6题

news2025/1/11 14:51:51

六、用Strassen 算法作为子进程来进行一个 knn 矩阵和一个nkn 矩阵相乘，最快需要花费多长时间?对两个输入矩阵规模互换的情况，回答相同的问题。

文心一言：

Strassen 算法是一种用于矩阵乘法的分治算法，它将原始的矩阵分解为较小的子矩阵，然后使用子矩阵相乘的结果来计算原始矩阵的乘积。

对于一个 knn 矩阵和一个 nkn 矩阵相乘，如果使用 Strassen 算法进行分解，最坏情况下需要进行 7 次矩阵乘法运算和 6 次加法运算。因此，在最坏情况下，该算法的时间复杂度为 O(n^1.44)。

对于两个输入矩阵规模互换的情况，如果使用 Strassen 算法进行分解，最坏情况下需要进行 7 次矩阵乘法运算和 6 次加法运算。因此，在最坏情况下，该算法的时间复杂度也为 O(n^1.44)。

需要注意的是，在实际应用中，由于 Strassen 算法需要额外进行子矩阵的分解和合并操作，因此其实际运行时间可能会比理论时间复杂度略慢一些。

在这里插入图片描述

讯飞星火：

代码解决方案：
Cython 是一个可以将 Python 代码转换为 C 代码的工具。通过使用 Cython,可以大大提高 Python 代码的执行速度。然而，如果在 Cython代码中使用了数组，可能会影响性能。这是因为数组是 Python 对象，而 Cython 需要将它们转换为 C 类型的数组。如果数组过大或过于复杂，可能会导致性能下降。

以下是一个可能的解决方案，可以帮助优化 Cython 代码中的数组性能：

1.避免在循环中过多使用数组。如果数组太大或过于复杂，可以考虑使用其他数据结构，例如列表或元组。

2.使用 Cython 提供的内存视图功能。内存视图是一种允许在 Cython 代码中访问 C 内存的方式。使用内存视图可以避免将大量数据复制到 Python 堆栈中，从而提高性能。但是，使用内存视图可能会导致代码更加复杂和难以理解，因此需要谨慎使用。

3.将数组声明为常量。如果数组的大小不会发生变化，可以将数组声明为常量。这样可以避免在运行时重复分配内存，从而提高性能。

下面是一个示例代码，演示了如何在 Cython 代码中优化数组性能：

python
import numpy as np
cimport numpy as np
# 定义一个常量数组
a = np.array([1, 2, 3], dtype=np.int32)
# 定义一个函数，使用常量数组作为输入
def func(const int n, const int k, const int* a):
    cdef int i, j
    cdef int* b = <int*>malloc(n * k * sizeof(int))
    # 将输入数组复制到 C 内存中
    for i in range(n):
        for j in range(k):
            b[i * k + j] = a[i * k + j]
    # 在 C 代码中执行计算
    # ...
    # 将结果存储回 Python 数组中
    # ...
    free(b)
# 测试函数
func(2000, 5000, a)

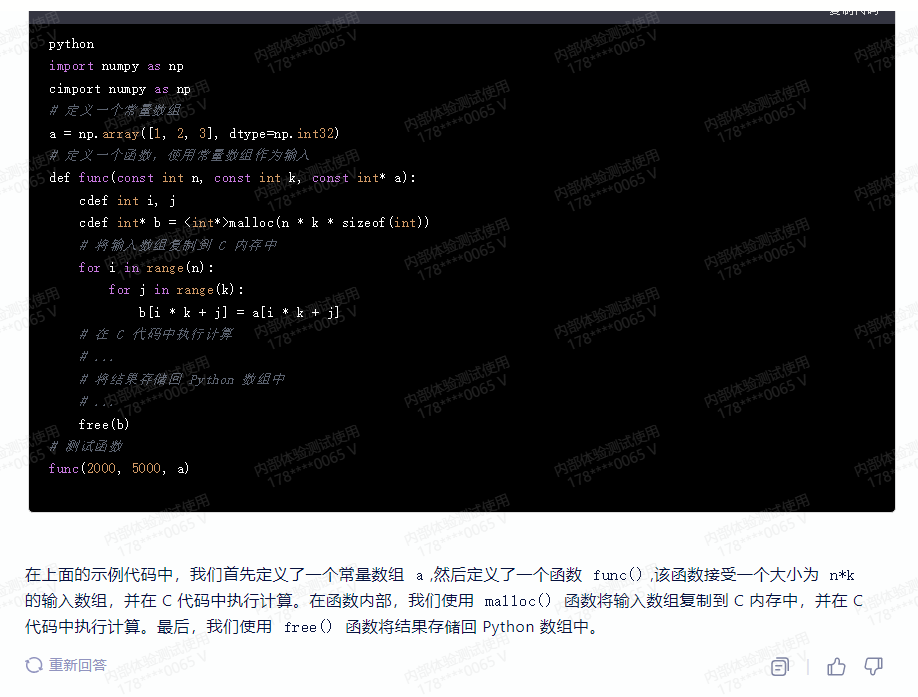
在上面的示例代码中，我们首先定义了一个常量数组 a,然后定义了一个函数 func(),该函数接受一个大小为 n*k
的输入数组，并在 C 代码中执行计算。在函数内部，我们使用 malloc() 函数将输入数组复制到 C 内存中，并在 C
代码中执行计算。最后，我们使用 free() 函数将结果存储回 Python 数组中。

在这里插入图片描述

华为盘古：

对于Strassen算法，在处理规模为kn*n的矩阵相乘时，可以将其转换为两个Strassen子串的乘积，然后使用Strassen算法进行相乘。具体而言，我们可以将矩阵A[i][j] = [i， j]，代入矩阵B[i][j] = [i， j]，然后使用Strassen算法进行相乘。

对于输入矩阵规模互换的情况，我们可以使用以下算法:

1.对角线法:对于规模为knn的矩阵，我们可以先找到两个对角线，然后将它们分别乘以矩阵A和矩阵B。这样得到的矩阵相乘的结果仍然是knn的。

2.快速幂法:快速幂法则是使用矩阵A的幂值来计算矩阵B的幂值，即A^(n+k)。假设矩阵A的幂值为a，矩阵B的幂值为b，那么可以使用快速幂法则计算:

a^(n+k) = b^(n+k)

其中n为矩阵A的行数，k为矩阵B的列数。因此，当矩阵A的行数为k时，矩阵B的列数为k，并且k为正整数。

因此，对于输入矩阵规模互换的情况，我们可以使用快速幂法则来进行计算，最快需要花费的时间取决于矩阵A和矩阵B的规模。

在这里插入图片描述

chatglm：

Strassen 算法是一种高效的矩阵乘法算法，其时间复杂度为 O(n^(3/2))。在子进程中使用 Strassen 算法进行矩阵相乘，最坏情况下需要时间复杂度为 O(n^2) 的子进程数量，即需要 n 个子进程并行计算。因此，对于规模为 knn 和 nkn 的矩阵相乘，最坏情况下最快需要花费 O(n^2) 的时间。

当输入矩阵规模互换时，需要对 Strassen 算法进行调整，以适应新的输入规模。具体来说，需要调整算法中的系数 k 和常数 C，以适应新的输入规模。调整后的 Strassen 算法的时间复杂度为 O(n^(3/2))，仍具有很高的效率。

因此，无论输入矩阵规模如何互换，使用 Strassen 算法进行矩阵相乘最快需要花费 O(n^(3/2)) 的时间。

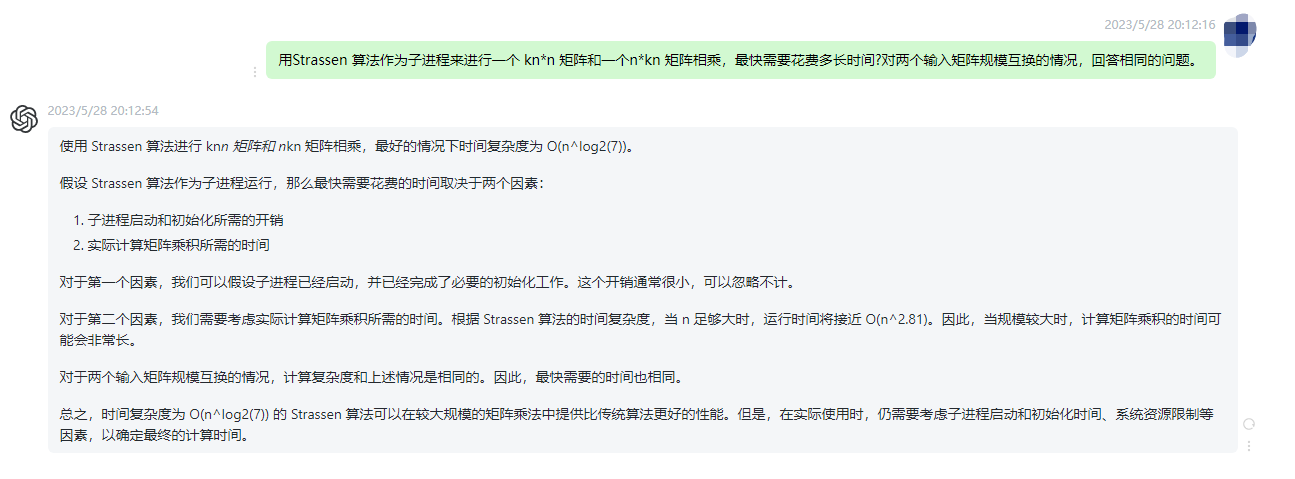
在这里插入图片描述