二叉树的基本操作

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，再来研究二叉树真正的创建方式，下面用左右孩子法来定义二叉树结构体。

二叉树的结构体及创建：

typedef int BTDataType;
typedef struct BinaryTreeNode
{
 BTDataType _data;
 struct BinaryTreeNode* _left;
 struct BinaryTreeNode* _right;
}BTNode;

void BinaryTreeCreate()
{
    BTNode* Node1 = BuyNode(1);
	BTNode* Node2 = BuyNode(2);
	BTNode* Node3 = BuyNode(3);
	BTNode* Node4 = BuyNode(4);
	BTNode* Node5 = BuyNode(5);
	BTNode* Node6 = BuyNode(6);
	BTNode* Node7 = BuyNode(7);
	Node1->left = Node2;
	Node2->left = Node4;
	Node1->right = Node3;
	Node2->right = Node5;
	Node3->right = Node6;
	Node3->left = Node7;
}

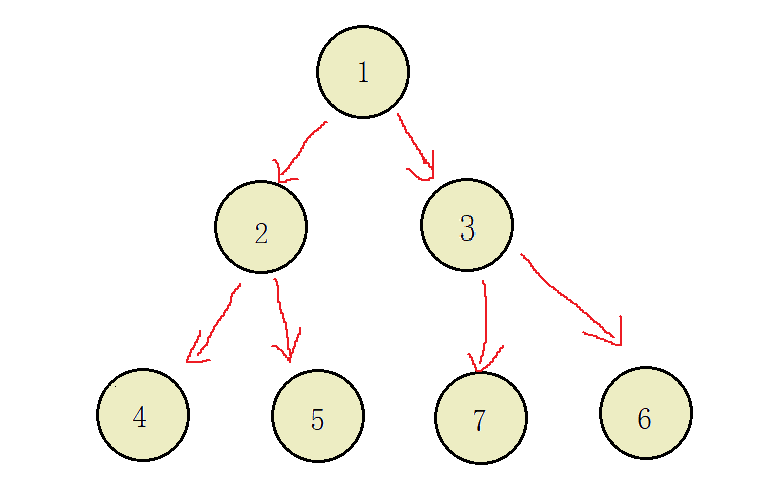
创建完二叉树的结构长这样

在这里插入图片描述

二叉树四大遍历

二叉树的遍历（traversing binary tree）是指从根结点出发按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次目仅被访问一次

二叉树的遍历方式有很多，我们来介绍常见的四种：

前序遍历：先访问根节点，再访问左子树，最后访问右子树。
中序遍历：先访问左子树，再访问根节点，最后访问右子树。
后序遍历：先访问左子树，再访问右子树，最后访问根节点。
层序遍历：按照从上到下，从左到右遍历二叉树

按照上面创建的二叉树，N代表空，如果是前序的话124NN5NN37NN6NN，中序就是，NN4NN52NN7NN631，后序就是N4N2N5N1N7N3N6N，层序就是1234576

二叉树的前序遍历：

如果二叉树为空，则返回空列表；
如果二叉树不为空，则先访问根节点，再前序遍历左子树，最后前序遍历右子树。

void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N");
		return;
	}
	printf("%c", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

二叉树的中序遍历：

如果二叉树为空，则返回空列表；
如果二叉树不为空，则先中序遍历左子树，再访问根节点，最后中序遍历右子树。

void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N");
		return;
	}
	BinaryTreeInOrder(root->left);
	printf("%d", root->data);
	BinaryTreeInOrder(root->right);
}

二叉树的后序遍历：

如果二叉树为空，则返回空列表；
如果二叉树不为空，则先后序遍历左子树，再后序遍历右子树，最后访问根节点。

void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N");
		return;
	}
	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%d", root->data);
}

二叉树的层序遍历：

层序遍历是这四种遍历中最难实现的一种，我们需要借助队列的先进先出特性来实现层序遍历，先讲根节点入队，随后抛出并输出，抛出的同时将根结点的左右孩子拿进队，以此类推，由于队列是先进先出，所以每次输出都是按照拿左右孩子的顺序按照从上到下从左到右进行输出。

如果二叉树为空，则返回空列表；
如果二叉树不为空，则先将根节点入队列，然后循环执行以下操作：
- 弹出队列头部节点，将其值加入结果列表；
- 如果该节点有左子节点，则将左子节点入队列；
- 如果该节点有右子节点，则将右子节点入队列。

void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q,root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%d", front->data);
		QueuePop(&q);
		if (front->left)
			QueuePush(&q,front->left);
		if (front->right)
			QueuePush(&q,front->right);
	}
}

二叉树的结点及高度

二叉树节点个数

如果二叉树为空，则结点个数为0；
如果二叉树不为空，则结点个数为根节点的个数加上左子树的结点个数和右子树的结点个数。

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

二叉树叶子节点个数

如果二叉树为空，则叶子节点个数为0；
如果二叉树不为空：
- 如果当前节点是叶子节点，则叶子节点个数为1；
- 如果当前节点不是叶子节点，则叶子节点个数为左子树的叶子节点个数加上右子树的叶子节点个数。

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

二叉树第k层节点个数

如果二叉树为空，则第k层节点个数为0；
如果k为1，则第k层节点个数为1；
如果k大于1，则第k层节点个数为左子树的第k-1层节点个数加上右子树的第k-1层节点个数。

int BinaryTreeLevelSize(BTNode* root,int k)
{
	assert(k > 0);
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BinaryTreeLevelSize(root->left,k-1)+ BinaryTreeLevelSize(root->right,k-1);
}

二叉树查找值为x的节点

如果二叉树为空，则返回空；
如果当前节点的值等于x，则返回当前节点；
否则，在左子树中递归查找值为x的节点，如果找到了，则返回找到的节点；否则，在右子树中递归查找值为x的节点，如果找到了，则返回找到的节点。

BTNode* BinaryTreeFind(BTNode* root,BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	BTNode* BinaryTreeLeft = BinaryTreeFind(root->left,x);
	if (BinaryTreeLeft)
		return BinaryTreeLeft;
	BTNode* BinaryTreeRight = BinaryTreeFind(root->right,x);
	if (BinaryTreeRight)
		return BinaryTreeRight;
	return NULL;
}