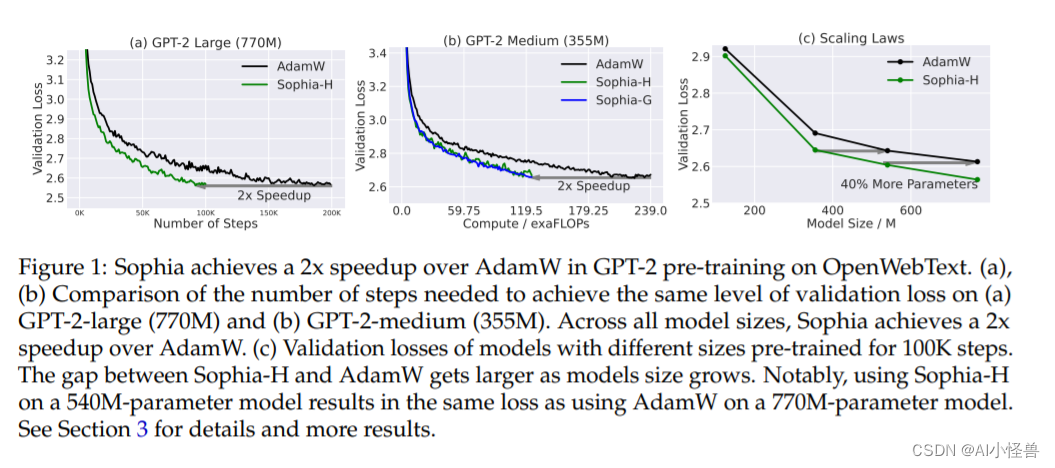
一、单目相机模型

在这里插入图片描述
上图为针孔相机成像原理，蓝色坐标中的O即为镜头光心。成像原理与小孔成像相同。

单目相机映射关系如下：

将上式进行变换，就可以从三位空间映射到2维平面的公式。

相机的畸变公式如下：

二、模型投影函数

void cv:projectPoints ( InputArray objectPoints, InputArray rvec, InputArray tvec, InputArray cameraMatrix,InputArray distCoeffs,outputArray imagePolints, jacobian =, OutputArray naArray(), double aspectRatio = 0)

objectPoints:世界坐标系中3D点的三维坐标。
rvec:世界坐标系变换到相机坐标系的旋转向量。
tvec:世界坐标系变换到相机坐标系的平移向量。
cameraMatrix:相机的内参矩阵。
distCoeffs:相机的畸变系数矩阵。
imagcPoints:三维坐标点在像素坐标系中估计的坐标。
jacobian:可选输出的雅可比矩阵。
aspectRatio:是否固定“宽高比”参数标志。
本节应用案例如下：

int main() {

	//输入计算的内参矩阵和畸变矩阵(在相机厂家说明或者标定获得)
	Mat cameraMatrix = (Mat_<float>(3, 3) << 532.016297, 0, 332.172519,
		0, 531.565159, 233.388075,
		0, 0, 1);

	Mat distCoeffs = (Mat_<float>(1, 5) << -0.285188, 0.080097, 0.001274,
		0.002415, 0.106579);

	//图像相机坐标系与世界坐标系之间的关系
	Mat rvec = (Mat_<float>(1, 3) << -1.977853, -2.002220, 0.130029);
	Mat tvec = (Mat_<float>(1, 3) << -26.88155, -42.79936, 159.19703);

	//生成第一张图像中内角点的三位世界坐标
	Size boardSize = Size(9,6);
	//棋盘格每个方格的真实尺寸
	Size squareSize = Size(10, 10);

	vector<Point3f> PointSets;
	for (int j = 0; j < boardSize.height; j++)
	{
		for (int k = 0; k < boardSize.width; k++)
		{
			Point3f realPoint;

			//假设标定板为世界坐标系的Z平面，及z=0
			realPoint.x = j * squareSize.width;
			realPoint.y = k * squareSize.height;
			realPoint.z = 0;
			PointSets.push_back(realPoint);
		}
	}

	//根据三维坐标和相机与世界坐标系时间的关系估计内角点像素坐标
	vector<Point2f> imagePoints;
	projectPoints(PointSets, rvec, tvec, cameraMatrix, distCoeffs, imagePoints);

	for (int i = 0; i < imagePoints.size(); i++)
	{
		cout << imagePoints[i] << endl;
	}

	waitKey(0);
	return 0;

}

三、单目相机标定

标定原理：
在这里插入图片描述
从上图中可以看出，相机坐标系可以通过世界坐标系进行平移变换来得到。具体的变换矩阵如相机坐标系右侧的公式。
标定板的图例如下：

上图中为两种类型的标定板，左侧为常用标定板，在提取的时候是内角点。而右侧标定板中不存在内角点，所以我们提取的是每个圆的中心点。
内角点提取函数如下：

bool cv:.findChessboardCorners ( InputArray image, Size patternSize, OutputArray corners, int flags = CALIB_CB_ADAPTIVE_THRESH+CALIB_CB_NORNALIZE_IPAGE)

image:含有棋盘标定板的图像，图像必须是CV_8U的灰度图像或者彩色图像。
patternSize:图像中棋盘内角点行数和列数
corners:检测到的角点坐标
flags:检测角点方式的标志
圆形标定板中心提取：

bool cv::findCirclesGrid ( InputArray image, Size patternSize, OutputArray centers, int flags, const Ptr< FeatureDetector > & blolbDetector, const CirclesGridFinderParameters & parameters)

image:输入含有圆形网格的图像，图像必须是CV_8U的灰度图像或者彩色图像。
patternSize:图像中每行和每列圆形的数目。
corners:输出的圆形中心坐标。
flags:检测圆心的操作标志。
blobDetector:在浅色背景中寻找黑色圆形斑点的特征探测器。
角点位置优化函数：

bool cv.find4QuadCornerSubpix ( InputArray img, InputOutputArray corners, size region_size)

img:计算出内角点的图像。
patternSize:内角点坐标。
corners:优化坐标时考虑的邻域范围。

绘制内角点提取的结果：

void cv::drawChessboardCorners ( InputOutputArray image, size patternSize, InputArray corners, bool patternWasFound)

image:需要绘制角点的目标图像，必须是CU_8U的彩色图像。patternSize:标定板每行和每列角点的数目。
corners:检测到的角点坐标数组。
pattern WasFound:是否显示找到完成的标定板标志。

相机标定函数：

double cv::calibrateCamera ( InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints,Size imageSize, InputOutputArray cameraMatrix, InputoutputArray distCoeffs, OutputArrayOfArrays     rvecs, OutputArrayOfArrays tvecs,int flags = 0, TermCriteria criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS,30,DBL_EPSILON)

objectPoints:棋盘格内角点的三维坐标。
imagePoints:棋盘格内角点在图像中的二维坐标。
imageSize:图像的像素尺寸大小。
cameraMatrix:相机的内参矩阵。
distCoeffs:相机的畸变系数矩阵。
rvecs:相机坐标系与世界坐标系之间的旋转向量。
tvecs:相机坐标系与世界坐标系之间的平移向量。
flags:选择标定算法的标志。
本节应用案例如下：
本案例中采用了两张标定板的提取图像：
在这里插入图片描述

并将两个图片的路径存放到ca.txt文件中

int main() {

	//读取图像
	vector<Mat>imgs;
	string imgName;

	//读取存放图片路径的txt文件
	ifstream fin("ca.txt");
	//挨个读取图片
	while(getline(fin, imgName))
	{
		Mat img = imread(imgName);
		imgs.push_back(img);
	}

	//方格标定板内角点的数目（行，列）
	Size board_size = Size(9, 6);

	//存放内角点坐标
	vector<vector<Point2f>> imgsPoints;

	//开始内角点提取
	for (int i = 0; i < imgs.size(); i++)
	{
		Mat img1 = imgs[i];
		Mat gray1;
		cvtColor(img1, gray1, COLOR_BGR2GRAY);
		vector<Point2f> img1_points;

		//计算标定板的角点
		findChessboardCorners(gray1, board_size, img1_points);
		//细化方格标定板角点坐标
		find4QuadCornerSubpix(gray1, img1_points, Size(5, 5));

		bool pattern = true;

		drawChessboardCorners(img1, board_size, img1_points, pattern);
		namedWindow("img1", WINDOW_NORMAL);
		imshow("img1", img1);
		waitKey(0);
		imgsPoints.push_back(img1_points);
	}

	//生成每个内角点的空间坐标
	Size squareSize = Size(10, 10);
	vector<vector<Point3f>> objectPoints;
	for (int i = 0; i < imgsPoints.size(); i++)
	{
		vector<Point3f> tempPointSet;
		for (int j = 0; j < board_size.height; j++)
		{
			for (int k = 0; k < board_size.width; k++)
			{
				Point3f realPoint;
				//设标定板为世界坐标系的z平面，即z=0
				realPoint.x = j * squareSize.width;
				realPoint.y = k * squareSize.height;
				realPoint.z = 0;
				tempPointSet.push_back(realPoint);
			}
		}
		objectPoints.push_back(tempPointSet);
	}

	//图像尺寸
	Size imageSize;
	imageSize.width = imgs[0].cols;
	imageSize.height = imgs[0].rows;

	//摄像机内参数矩阵
	Mat cameraMatrix = Mat(3, 3, CV_32FC1, Scalar::all(0));

	//摄像机的5个畸变系数：k1,k2,p1,p2,k3
	Mat distCoeffs = Mat(1, 5, CV_32FC1, Scalar::all(0));

	//每幅图像的旋转向量、平移量
	vector<Mat>  rvecs, tvecs;

	calibrateCamera(objectPoints, imgsPoints, imageSize, cameraMatrix, distCoeffs, rvecs, tvecs, 0);
	cout << "相机的内参矩阵：" << cameraMatrix << endl;
	cout << "相机畸变系数：" << distCoeffs << endl;
	waitKey(0);
	return 0;
}

最终的运行结果如下图：
在这里插入图片描述
这里只放一张图像。最终的输出结果为：

相机的内参矩阵：[120.8643306554273, 0, 94.55565247064737;
 0, 119.979406894919, 55.48571212317609;
 0, 0, 1]
相机畸变系数：[-0.5559208449775317, 3.15840209023594, -0.001816753642197531, -0.01817901488786, -7.629569308066959]