(转载)基于遗传算法的TSP算法(matlab实现)

news2024/11/25 20:20:10

1 理论基础

TSP(traveling salesman problem,旅行商问题)是典型的NP完全问题，即其最坏情况下的时间复杂度随着问题规模的增大按指数方式增长，到目前为止还未找到一个多项式时间的有效算法。

TSP问题可描述为：已知n个城市相互之间的距离，某一旅行商从某个城市出发访问每个城市一次且仅一次，最后回到出发城市，如何安排才使其所走路线最短。简言之，就是寻找一条最短的遍历n个城市的路径，或者说搜索自然子集X={1,2,…,n}(X的元素表示对n个城市的编号)的一个排列π(X)={V1,V2,…,Vn},使

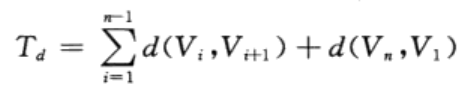
取最小值，其中d(Vi,Vi+1)表示城市Vi到城市Vi+1的距离。

TSP问题并不仅仅是旅行商问题，其他许多的NP完全问题也可以归结为TSP问题，如邮路问题、装配线上的螺母问题和产品的生产安排问题等，使得TSP问题的有效求解具有重要的意义。

2 案例背景

2.1 问题描述

本案例以14个城市为例，假定14个城市的位置坐标如表4-1所列。寻找出一条最短的遍历14个城市的路径。

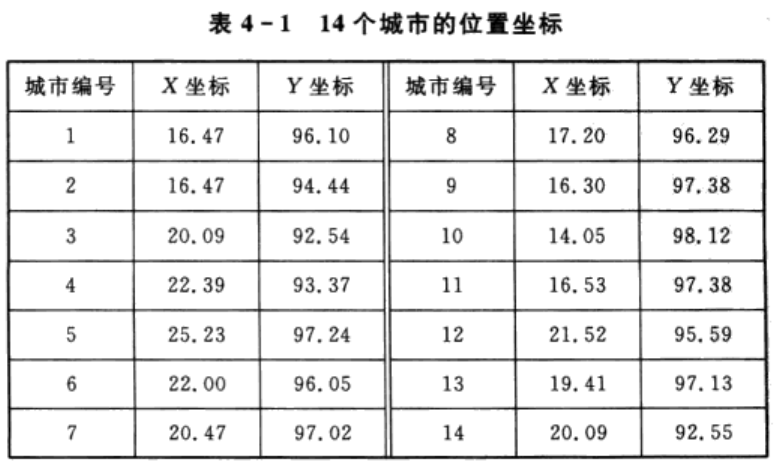
2.2 解决思路及步骤

1.算法流程

遗传算法TSP问题的流程图如图4-1所示。

2.遗传算法实现

(1)编码

采用整数排列编码方法。对于n个城市的TSP问题，染色体分为n段，其中每一段为对应城市的编号，如对10个城市的TSP问题{1,2,3,4,5,6,7,8,9,10},则|1|10|2|4|5|6|8|7|9|3就是一个合法的染色体。

(2)种群初始化

在完成染色体编码以后，必须产生一个初始种群作为起始解，所以首先需要决定初始化种群的数目。初始化种群的数目一般根据经验得到，一般情况下种群的数量视城市规模的大小而确定，其取值在50～200之间浮动。

(3)适应度函数

设k1|k2I…|ki|…|kn|为一个采用整数编码的染色体，Dkikj为城市ki到城市kj的距离，则该个体的适应度为

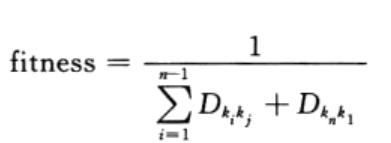
即适应度函数为恰好走遍n个城市，再回到出发城市的距离的倒数。优化的目标就是选择适

应度函数值尽可能大的染色体，适应度函数值越大的染色体越优质，反之越劣质。

(4)选择操作

选择操作即从旧群体中以一定概率选择个体到新群体中，个体被选中的概率跟适应度值有关，个体适应度值越大，被选中的概率越大。

(5)交叉操作

采用部分映射杂交，确定交叉操作的父代，将父代样本两两分组，每组重复以下过程(假定城市数为10):

①产生两个[1,10]区间内的随机整数r1和r2,确定两个位置，对两位置的中间数据进行交叉，如r1=4,r2=7

②交叉后，同一个个体中有重复的城市编号，不重复的数字保留，有冲突的数字(带*位置)采用部分映射的方法消除冲突，即利用中间段的对应关系进行映射。结果为

(6)变异操作

变异策略采取随机选取两个点，将其对换位置。产生两个[1,10]范围内的随机整数r1和 r2,确定两个位置，将其对换位置，如r1=4,r2=7

(7)进化逆转操作

为改善遗传算法的局部搜索能力，在选择、交叉、变异之后引进连续多次的进化逆转操作。这里的“进化”是指逆转算子的单方向性，即只有经逆转后，适应度值有提高的才接受下来，否则逆转无效。产生两个[1,10]区间内的随机整数r1和r2,确定两个位置，将其对换位置，如r1=4, r2=7

对每个个体进行交叉变异，然后代入适应度函数进行评估，x选择出适应值大的个体进行下一代的交叉和变异以及进化逆转操作。循环操作：判断是否满足设定的最大遗传代数MAXGEN,不满足则跳入适应度值的计算；否则，结束遗传操作。

3 MATLAB程序实现

完整代码可以从下面的链接中获取

基于遗传算法的TSP算法（matlab代码）

4 结果分析

优化前的一个随机路线轨迹图如图4-2所示。

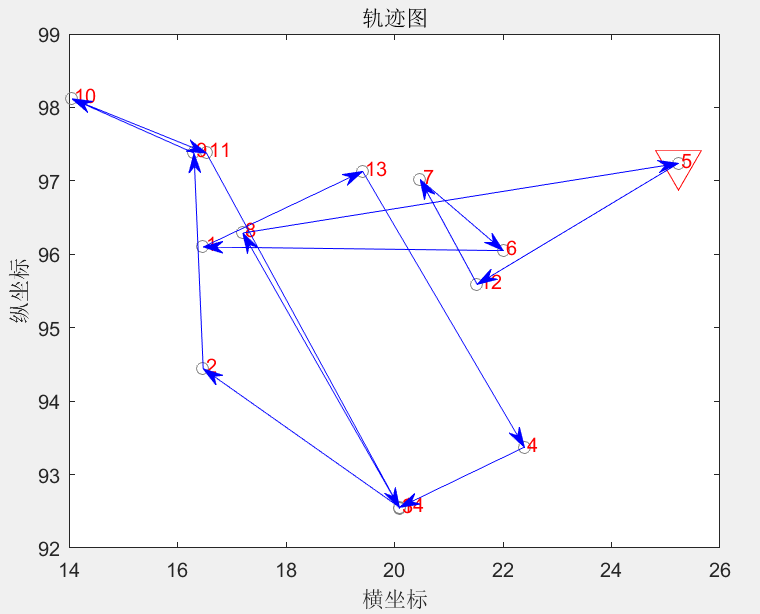
图4-2 随机路线

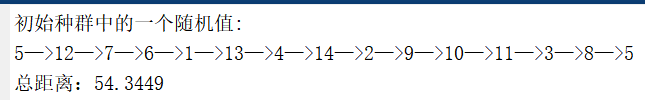
优化后的路线如图4-3所示：

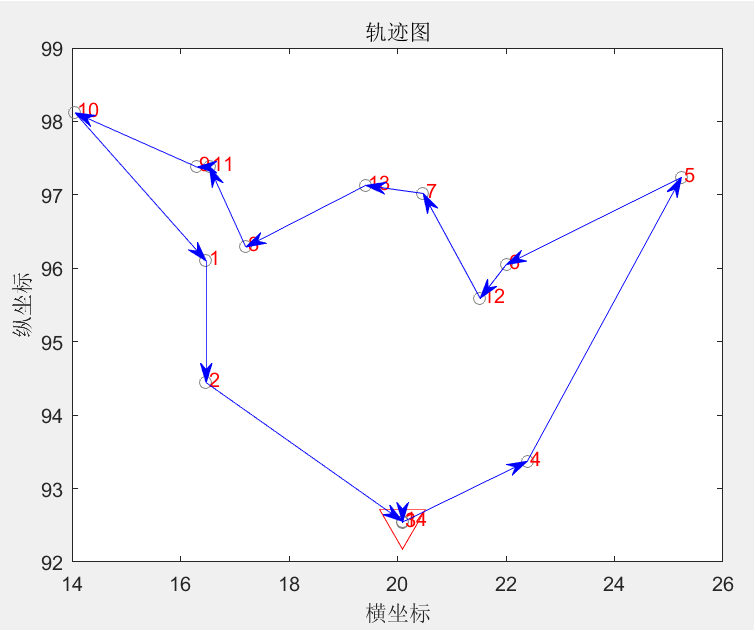
图4-3 优化后的线路

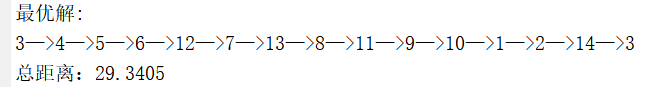
迭代过程如图4-4所示：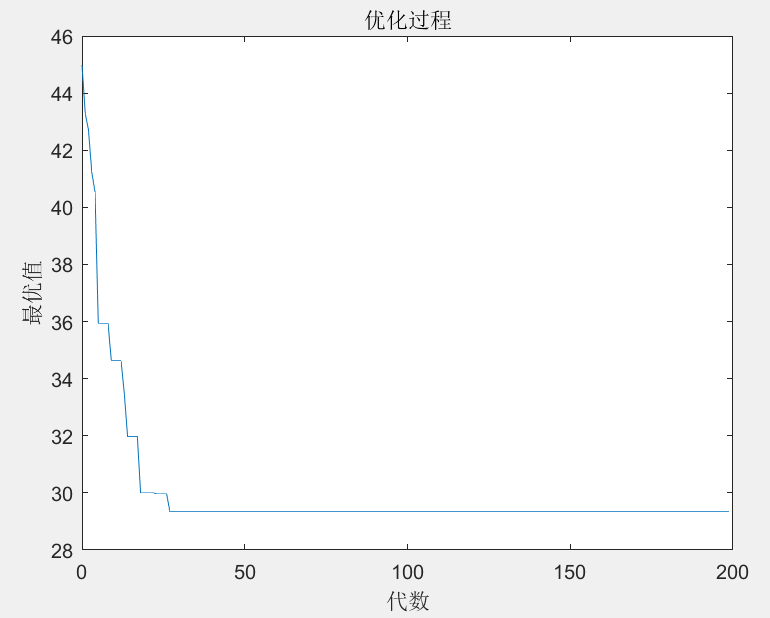

图4-4 迭代过程

5 延伸阅读

5.1 应用扩展

以下问题都与TSP问题一致，都可以使用上述方法解决。

1.装配线上的螺母问题

在一条装配线上用一个机械手去紧固待装配部件上的螺母问题。机械手由其初始位置(该位置在第一个要紧固的螺母的上方)开始，依次移动到其余的每一个螺母，最后返回到初始位置。机械手移动的路线就是以螺母为结点的一条周游路线。一条最小成本周游路线将使机械手完成工作所用的时间取最小值。注意：只有机械手移动的时间总量是可变化的。

2.产品的生产安排问题

假设要在同一组机器上制造n种不同的产品，生产是周期性进行的，即在每一个生产周期

这n种产品都要被制造。要生产这些产品有两种开销，一种是制造第i种产品时所耗费的资

金(1≤i≤n),称为生产成本；另一种是这些机器由制造第i种产品变到制造第j种产品时所

耗费的开支C;,称为转换成本。显然，生产成本与生产顺序无关。于是，希望找到一种制造这

些产品的顺序，使得制造这n种产品的转换成本和为最小。

5.2 遗传算法的改进

上述程序中，对遗传算法做了以下两处改进。

1.使用精英策略

子代种群中的最优个体永远不会比父代最优的个体差，这样使得父代的好的个体不至于

由于交叉或者变异操作而丢失。

2.使用进化逆转操作

在本文的编码中，每一个染色体即对应一个TSP环游，如果染色体码串的顺序发生变化，则环游路径也随之改变。因此，TSP问题解的关键地方就是码串的顺序。对照文中的交叉算子，可以发现，纵使两个亲代完全相同，通过交叉，仍然会产生不同于亲代的子代，且子代的码串排列顺序与亲代有较大的差异。交叉算子的这种变异效果所起的作用有两个方面，一方面它能起到维持群体内一定的多样性的作用，避免陷入局部最优解；但是另一方面，它却不利于子代继承亲代的较多信息，特别是当进化过程进入到后期，群体空间中充斥着大量的高适应度个体，交叉操作对亲代的较优基因破坏很大，使子代难以继承到亲代的优良基因，从而使交叉算子的搜索能力大大降低。

同交叉算子相比较，逆转算子能使子代继承亲代的较多信息。假设码串为123456789,在2和3,6和7之间发生两处断裂再逆转插入，则新码串为12-6543-789,此时子代中12段、6543段、789段与亲代对应片段顺序完全一样(6543与3456顺序对于环游路径长度来说是等价的),只是在断裂点的两端环游次序发生了变化，而且本文中逆转是单方向的，即只接受朝着好的方向的逆转，因此它搜索最优解的能力强于交叉算子。